Injectivity of compressing maps on the set of primitive sequences modulo square-free odd integers

Abstract

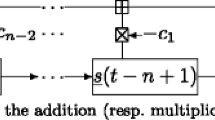
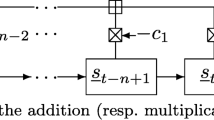
Let p ₁, p ₂,…,p _r be distinct odd primes and m = p ₁ p ₂⋯p _r . Let f(x) be a primitive polynomial of degree n over $\mathbb {Z}/m\mathbb {Z}$. Denote by L(f) the set of primitive linear recurring sequences generated by f(x). A map ψ on $\mathbb {Z}/m\mathbb {Z}$ naturally induces a map $\widehat {\psi }$ on L(f), mapping a sequence $(\dots ,\underline {s}({i-1}),\underline {s}(i),\underline {s}({i+1}),\dots )$ to $(\dots ,\psi (\underline {s}({i-1})),\psi (\underline {s}(i)),\psi (\underline {s}({i+1})),\dots )$. Previous results gave sufficient conditions under which modular functions induce injective maps on L(f). In this article we give an inequality which holds for large enough n. If this inequality holds, then the injectivity of $\hat {\psi }$ is clearly determined for any map ψ on $\mathbb {Z}/m\mathbb {Z}$. Particularly, the modular function ψ(a)=a mod M induces an injective map on L(f) for any $M\in \left \{{2\leq i\in \mathbb {Z}:i \nmid m}\right \}$.