Skip to main content

Advertisement

Springer Nature Link
Log in

Generic attacks with standard deviation analysis on a-feistel schemes

  • Published:
Cryptography and Communications Aims and scope Submit manuscript

Abstract

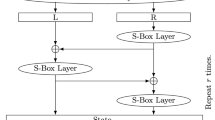
A usual way to construct block ciphers is to apply several rounds of a given structure. Many kinds of attacks are mounted against block ciphers. Among them, differential and linear attacks are widely used. Vaudenay showed that ciphers achieving perfect pairwise decorrelation are secure against linear and differential attacks. It is possible to obtain such schemes by introducing at least one random affine permutation as a round function in the design of the scheme. In this paper, we study attacks on schemes based on classical Feistel schemes where we introduce one or two affine permutations. Since these schemes resist against linear and differential attacks, we will study attacks based on specific equations on 4-tuples of plaintext/ciphertext messages. We show that these schemes are stronger than classical Feistel schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Biham, E., Shamir, A.: Differential cryptanalysis of DES-like cryptosystems. In: Menezes, A. , Vanstone, P.S.A. (eds.) Advances in Cryptology – CRYPTO 1990, vol. 537 of Lecture Notes in Computer Science, pp 2–21. Springer (1991)

  2. Biham, E., Shamir, A.: Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 4(1), 3–72 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  3. Gilbert, H., Minier, M.: New results on the pseudorandomness of some blockcipher constructions. In: Matsui, M. (ed.) Fast Software Encrytion – FSE ’01, vol. 2355 of Lecture Notes in Computer Science, pp 248–266. Springer (2001)

  4. Hoel, P.G., Port, S.C., Stone, C.J.: Introduction to Probability Theory. Houghton Mifflin Company (1971)

  5. Jutla, C.S.: Generalized birthday attacks on unbalanced feistel networks. In: Krawczyk, H. (ed.) Advances in Cryptology – CRYPTO ’98, vol. 1462 of Lecture Notes in Computer Science, pp 186–199. Springer (1998)

  6. Knudsen, L.R.: DEAL - A 128-Bit Block Cipher. Technical Report 151, University of Bergen, Department of Informatics, Norway (1998)

    Google Scholar 

  7. Luby, M., Rackoff, C.: How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Comput. 17(2), 373–386 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  8. Lucks, S.: Faster luby-rackoff ciphers. In: Gollman, D. (ed.) Fast Software Encryption – FSE ’96, vol. 1039 of Lecture Notes in Computer Science, pp 189–203. Springer (1996)

  9. Matsui, M.: Linear cryptanalysis methods for DES cipher. In: Goos, G., Hartmanis, J. (eds.) Advances in Cryptology – EUROCRYPT 1993, vol. 765 of Lecture Notes in Computer Science, pp 386–397. Springer (1994)

  10. Matsui, M.: The first experimental cryptanalysis of the data encryption standard. In: Goos, G., Hartmanis, J. (eds.) Advances in Cryptology – CRYPTO 1994, vol. 869 of Lecture Notes in Computer Science, pp 1–11. Springer (1994)

  11. Nachef, V., Patarin, J., Treger, J.: Generic attacks on misty schemes. In: Abdalla, M., Barretol, P.S.L.M. (eds.) Progress in Cryptology – LATINCRYPT 2010, vol. 6212 of Lecture Notes in Computer Science, pp 222–240. Springer (2010)

  12. Nachef, V., Volte, E., Patarin, J.: Differential attacks on generalized feistel schemes. In: Abdalla, M., Nita-Rotaru, C. , Dahab, R. (eds.) CANS 2013, vol. 8257 of Lecture Notes in Computer Science, pp 1–19. Springer (2013)

  13. Naor, M., Reingold, O.: On the construction of pseudorandom permutations: Luby-rackoff revisited. J. Cryptol. 12(1), 29–66 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  14. Patarin, J.: Generic attacks on feistel schemes. In: Boyd, C. (ed.) Advances in Cryptology – ASIACRYPT 2001, vol. 2248 of Lecture Notes in Computer Science, pp 222–238. Springer (2001)

  15. Patarin, J., Nachef, V., Berbain, C.: Generic attacks on unbalanced feistel schemes with contracting functions. In: Lai, X., Chen, K. (eds.) Advances in Cryptology – ASIACRYPT 2006, vol. 4284 of Lecture Notes in Computer Science, pp 396–411. Springer (2006)

  16. Schneier, B., Kelsey, J.: Unbalanced feistel networks and block cipher design. In: Gollmann, D. (ed.) Fast Software Encrytion – FSE ’96, vol. 1039 of Lecture Notes in Computer Science, pp 121–144. Springer (1996)

  17. Treger, J., Patarin, J.: Generic attacks on feistel networks with internal permutations. In: Preneel, B. (ed.) Progresses in Cryptology – AFRICACRYPT ’09, Lecture Notes in Computer Science. Springer (2009)

  18. Vaudenay, S.: Provable security for block ciphers by decorralation. In: Movan, M., Meinel, C., Krob, D. (eds.) STACS 1998, vol. 1373 of Lecture Notes in Computer Science, pp 249–265. Springer (1998)

  19. Vaudenay, S.: Decorrelation: A theory for block cipher security. J. Cryptol. 16 (4), 249–286 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  20. Volte, E., Nachef, V., Marrière, N.: Improvements of attacks on various feistel schemes. In: MYCRYPT 2016, Lecture Notes in Computer Science. Springer (2016)

  21. Volte, E., Nachef, V., Patarin, J.: Improved generic attacks on unbalanced feistel schemes with expanding functions. In: Abe, M. (ed.) Advances in Cryptology – ASIACRYPT 2010, vol. 6477 of Lecture Notes in Computer Science, pp 94–111. Springer (2010)

Download references

Acknowledgements

The authors want to thank the anonymous referee for the KPA on φ ∘ Ψ(f 1) with \((n+1)2^{\frac {n}{2}}\) messages.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Cergy-Pontoise, CNRS UMR 8088, 2 Avenue Adolphe Chauvin, 95011, Cergy-Pontoise Cedex, France

    Valérie Nachef & Emmanuel Volte

  2. Laboratoire de Mathématiques de Versailles, UVSQ CNRS, Université de Paris-Saclay, 78035, Versailles, France

    Jacques Patarin

Authors
  1. Valérie Nachef
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jacques Patarin
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Emmanuel Volte
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Valérie Nachef.

Additional information

This article is part of the Topical Collection on Recent Trends in Cryptography

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nachef, V., Patarin, J. & Volte, E. Generic attacks with standard deviation analysis on a-feistel schemes. Cryptogr. Commun. 10, 59–77 (2018). https://doi.org/10.1007/s12095-017-0244-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12095-017-0244-7

Keywords

Mathematics Subject Classification (2010)