Skip to main content
SpringerLink
Log in

New z-complementary/complementary sequence sets with non-power-of-two length and low PAPR

  • Published:
Cryptography and Communications Aims and scope Submit manuscript

Abstract

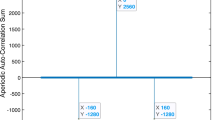
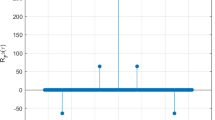
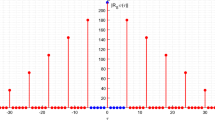
Sequences with low peak-to-average power ratio (PAPR) and desirable lengths are useful and important for orthogonal frequency division multiplexing (OFDM) systems. In this paper, based on the generalized Boolean functions (GBFs), a class of q-ary Z-complementary sequence sets (ZCSSs) and a class of complementary sequence sets (CSSs) are constructed. The obtained new ZCSSs and CSSs have low PAPR and non-power-of-two lengths.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Golay, M.J.E.: Static multislit spectrometry and its application to the panoramic display of infrared spectra. J. Opt. Soc. Amer. 41(7), 468–472 (1951)

    Article  Google Scholar 

  2. Spasojevic, P., Georghiades, C.N.: Complementary sequences for ISI channel estimation. IEEE Trans. Inf. Theory 47(3), 1145–1152 (2001)

    Article  MathSciNet  Google Scholar 

  3. Li, S., Wu, H., Jin, L., Wei, S.: Construction of compressed sensing matrix based on complementary sequence. In: IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, pp 23–27 (2017)

  4. Pezeshki, A., Calderbank, A.R., Moran, W., Howard, S.D.: Doppler resilient Golay complementary waveforms. IEEE Trans. Inf. Theory 54(9), 4254–4266 (2008)

    Article  MathSciNet  Google Scholar 

  5. Davis, J.A., Jedwab, J.: Peak-to-mean power control in OFDM, Golay complementary sequences and Reed-Muller codes. IEEE Trans. Inf. Theory 45(7), 2397–2417 (1999)

    Article  MathSciNet  Google Scholar 

  6. Budišin, S.: New complementary pairs of sequences. Electron. Lett. 26(13), 881–883 (1990)

    Article  Google Scholar 

  7. Budišin, S., Spasojevic, P.: Paraunitary generation/correlation of QAM complementary sequence pairs. Cryptography Commun. 6(1), 59–102 (2014)

    Article  MathSciNet  Google Scholar 

  8. Ma, D.X., Wang, Z.L., Gong, G., Li, H.: A new method to construct Golay complementary set by paraunitary matrices and Hadamard matrices. In: 9th International Conference on Sequences and Their Applications (SETA-2016), pp 1–12 (2016)

  9. Borwein, P.B., Ferguson, R.A.: A complete description of Golay pairs for lengths up to 100. Math. Comput. 73, 967–985 (2003)

    Article  MathSciNet  Google Scholar 

  10. Tseng, C.C., Liu, C.L.: Complementary sets of sequences. IEEE Trans. Inf. Theory 18(5), 644–652 (1972)

    Article  MathSciNet  Google Scholar 

  11. Paterson, K.G.: Generalized Reed-Muller codes and power control in OFDM modulation. IEEE Trans. Inf. Theory 46(1), 104–120 (2000)

    Article  MathSciNet  Google Scholar 

  12. Welti, G.: Quaternary codes for pulsed radar. IRE Trans. Inf. Theory 6(3), 400–408 (1960)

    Article  Google Scholar 

  13. Wang, S.Q., Abdi, A.: Aperiodic complementary sets of sequences-based MIMO frequency selective channel estimation. IEEE Commun. Lett. 9 (10), 891–893 (2005)

    Article  Google Scholar 

  14. Wang, S., Abdi, A.: MIMO ISI channel estimation using uncorrelated Golay complementary sets of polyphase sequences. IEEE Trans. Vehi. Techno. 56(5), 3024–3040 (2007)

    Article  Google Scholar 

  15. Jeon, H., Lee, J., Han, Y., Kim, S.J., Kweon, I.S.: Multi-image deblurring using complementary sets of fluttering patterns. IEEE Trans. Image Proc. 26(5), 2311–2326 (2017)

    Article  MathSciNet  Google Scholar 

  16. Chen, C.Y.: Complementary sets of non-power-of-two length for peak-to-average power ratio reduction in OFDM. IEEE Trans. Inf. Theory 62(12), 7538–7545 (2016)

    Article  MathSciNet  Google Scholar 

  17. Aparicio, J., Shimura, T.: Asynchronous detection and identification of multiple users by multi-carrier modulated complementary set of sequences. IEEE Access 6, 22054–22069 (2018)

    Article  Google Scholar 

  18. Fan, P.Z., Yuan, W.N., Tu, Y.F.: Z-complementary binary sequences. IEEE Signal Proc. Lett. 14(8), 509–512 (2007)

    Article  Google Scholar 

  19. Liu, Z.L., Parampalli, U., Guan, Y.L.: Optimal odd-length binary Z-complementary pairs. IEEE Trans. Inf. Theory 60(9), 5768–5781 (2014)

    Article  MathSciNet  Google Scholar 

  20. Lee, W.: Mobile Communications Design Fundamentals. Wiley, Hoboken (2010)

    Google Scholar 

  21. Liu, Z.L., Guan, Y.L.: 16-QAM almost-complementary sequences with low PMEPR. IEEE Trans. Commun. 64(2), 668–679 (Jan. 2016)

  22. Yu, N.Y., Gong, G.: Near-complementary sequences with low PMEPR for peak power control in multicarrier communications. IEEE Trans. Inf. Theory 57(1), 505–513 (2011)

    Article  MathSciNet  Google Scholar 

  23. Chen, C.Y., Wang, C.H., Chao, C.C.: Complementary sets and Reed-Muller codes for peak-to-average power ratio reduction in OFDM. In: Proc. 16th AAECC Lect. Notes Comput. Sci., vol. 3857, pp 317–327 (2006)

  24. Chen, C.Y., Wang, C.H., Chao, C.C.: Complete complementary codes and generalized Reed-Muller codes. IEEE Commun. Lett. 12(11), 849–851 (2008)

    Article  Google Scholar 

  25. Chen, W., Tellambura, C.: Identifying a class of multiple shift complementary sequences in the second order cosets of the first order Reed-Muller codes. In: IEEE Int. Conf. Commun., vol. 1, Seoul, South Korea, pp. 618–621 (2005)

  26. Schmidt, K.-U.: Complementary sets, generalized Reed-Muller codes, and power control for OFDM. IEEE Trans. Inf Theory 53(2), 808–814 (2007)

    Article  MathSciNet  Google Scholar 

  27. Chen, C.Y.: A novel construction of complementary sets with flexible lengths based on Boolean functions. IEEE Commun. Lett. 22(2), 260–263 (2018)

    Article  Google Scholar 

  28. Adhikary, A.R., Majhi, S.: New constructions of complementary sets of sequences of lengths non-power-of-two. IEEE Commun. Lett. 23(7), 1119–1122 (2019)

    Article  Google Scholar 

  29. Wang, G.X., Adhikary, A.R., Zhou, Z.C., Yang, Y.: Generalized constructions of complementary sets of sequences of lengths non-power-of-two. IEEE Signal Proc. Lett. 27, 136–140 (2020)

    Article  Google Scholar 

  30. Shen, B.S., Yang, Y., Zhou, Z.C.: A construction of binary Golay complementary sets based on even-shift complementary pairs. IEEE Access 8, 29882–29890 (2020)

    Article  Google Scholar 

  31. Pai, C.Y., Chen, C.Y.: Construction of complementary sequence sets based on complementary pairs. IEEE Access 56(8), 966–968 (2020)

    Google Scholar 

  32. Liu, Z.L., Parampalli, U., Guan, Y.L.: On even-period binary Z-complementary pairs with large ZCZs. IEEE Signal Process. Lett. 21(3), 284–287 (2014)

    Article  Google Scholar 

  33. Liu, Z.L., Parampalli, U., Guan, Y.L.: Optimal odd-length binary Z-complementary pairs. IEEE Trans. Inf. Theory 21(3), 284–287 (2014)

    MathSciNet  MATH  Google Scholar 

  34. Chen, C.Y.: A novel construction of Z-complementary pairs based on generalized Boolean functions. IEEE Signal Process. Lett. 24(7), 284–287 (2017)

    Article  Google Scholar 

  35. Adhikary, A.R., Majhi, S., Liu, Z.L., Guan, Y.L.: New sets of even-length binary Z-complementary pairs with asymptotic ZCZ ratio of 3/4. IEEE Signal Process. Lett. 25(7), 970–973 (2018)

    Article  Google Scholar 

  36. Xie, C.L., Sun, Y.J.: Constructions of even-period binary Z-complementary pairs with large ZCZs. IEEE Signal Process. Lett. 25(8), 1141–1145 (2018)

    Article  Google Scholar 

  37. Shen, B.S., Yang, Y., Zhou, Z.C., Fan, P.Z., Guan, Y.L.: New optimal binary Z-complementary pairs of odd length 2m+ 3. IEEE Signal Proc. Lett. 26(12), 1931–1934 (2019a)

    Article  Google Scholar 

  38. Shen, B.S., Yang, Y., Zhou, Z.C., Zhou, Y.J.: New constructions of binary (near) complementary sets. In: The 9th International Workshop on Signal Design and its Applications in Communications (IWSDA’19), October 20-24 Dongguan, China, pp 1–5 (2019b)

  39. Adhikary, A.R., Sarkar, P., Majhi, S.: A direct construction of q-ary even length Z-complementary pairs using generalized Boolean functions. IEEE Signal Process. Lett. 27, 146–150 (2020)

    Article  Google Scholar 

  40. Pai, C.Y., Majhi, S., Shing, W.W., Chen, C.Y.: Z-complementary pairs with flexible lengths from generalized Boolean functions. IEEE Commun. Lett. 24(6), 1183–1187 (2020)

    Article  Google Scholar 

  41. Gu, Z., Zhou, Z.C., Wang, Q., Fan, P.Z.: New construction of optimal Type-II binary Z-complementary pairs. IEEE Trans. Inf. Theory, Early Access Article (2021)

  42. Yu, T., Du, X.Y., Li, L.P., Yang, Y.: Constructions of even-length Z-complementary pairs with large zero correlation zones. IEEE Signal Proc. Lett. 28, 828–831 (2021)

    Article  Google Scholar 

  43. Sarkar, P., Roy, A., Majhi, S.: Construction of Z-complementary code sets with non-power-of-two lengths based on generalized Boolean functions. IEEE Commun. Lett. 24(8), 1607–1611 (2020)

    Article  Google Scholar 

Download references

Acknowledgments

The authors are very grateful to the reviewers and the Associate Editor for their valuable comments and suggestions that improved the presentation and quality of this paper. This work of B.S. Shen, Y. Yang and Z.C. Zhou was supported in part by the NSFC Project No. 62171389 and 62131016. The work of Pingzhi Fan was supported by the NSFC project No. 62020106001 and the 111 project No. 111-2-14.

Author information

Authors and Affiliations

  1. School of Mathematics, Southwest Jiaotong University, Chengdu, China

    Bingsheng Shen, Pingzhi Fan & Zhengchun Zhou

  2. Key Lab of Information Coding and Transmission, Southwest Jiaotong University, Chengdu, China

    Yang Yang

Authors
  1. Bingsheng Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yang Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pingzhi Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhengchun Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yang Yang.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This paper was presented in part at the 2019 Ninth International Workshop on Signal Design and its Applications in Communications (IWSDA) [38]

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shen, B., Yang, Y., Fan, P. et al. New z-complementary/complementary sequence sets with non-power-of-two length and low PAPR. Cryptogr. Commun. 14, 817–832 (2022). https://doi.org/10.1007/s12095-021-00550-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12095-021-00550-7

Keywords

Mathematics Subject Classification (2010)

Search

Navigation