Skip to main content

Advertisement

Springer Nature Link
Log in

Group Method of Data Handling to Predict Scour at Downstream of a Ski-Jump Bucket Spillway

  • Research Article
  • Published:
Earth Science Informatics Aims and scope Submit manuscript

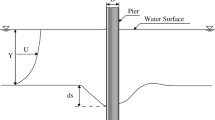
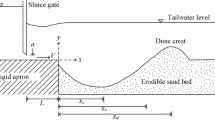
Abstract

This study introduces a method to predict scour hole geometry at downstream of a ski-jump bucket by group method of data handling (GMDH). The GMDH network was developed using evolutionary and iterative algorithms including those of genetic programming (GP), particle swarm optimization (PSO), and back propagation (BP) algorithms. Results of alternative GMDH networks were compared with those obtained using artificial neural networks, genetic programming, ANFIS, empirical equations, and regression-based equations. Performances indicated that proposed GMDH-BP produced more accurate results in comparison with other methods. Moreover, the most effective independent parameters on scour hole geometry were determined using sensitivity analysis. Finally, combination of evolutionary and iterative algorithms has been confirmed that the GMDH network is a useful soft computing tool for prediction of scour hole geometry at downstream of a ski-jump bucket.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Abdel-Aal RE, El-alfy E-SM (2009) Constructing optimal educational tests using GMDH-based item ranking and selection. Neurocomputing 72:1184–1197

    Google Scholar 

  • Alavi AH, Gandomi AH (2011) A robust data mining approach for formulation of geotechnical engineering systems. International Journal for Computer-Aided Engineering and Software-Engineering Computations, Emerald 28(3):242–274

    Google Scholar 

  • Alavi AH, Gandomi AH (2012) Energy-based models for assessment of soil liquefaction. Geoscience Frontiers, Elsevier 3(4):541–555

    Article  Google Scholar 

  • Alavi AH, Gandomi AH, Sahab MG, Gandomi M (2010) Multi expression programming: A new approach to formulation of soil classification. Engineering with Computers, Springer 26(2):111–118

    Article  Google Scholar 

  • Amanifard N, Nariman-Zadeh N, Farahani MH, Khalkhali A (2008) Modeling of multiple short-length-scale stall cells in an axial compressor using evolved GMDH neural networks. J Energ Convers Manage 49(10):2588–2594

    Google Scholar 

  • Amanifard N, Nariman-Zadeh N, Farahani MH, Khalkhali A (2009) Modelling of multiple short-length-scale stall cells in an axial compressor using evolved GMDH neural networks. Energy Conversion and Management 49(10):2588–2594

    Article  Google Scholar 

  • Astakhov VP, Galitsky VV (2005) Tool life testing in gundrilling: an application of the group method of data handling (GMDH). Int J Mach Tool Manu 45:509–517

    Google Scholar 

  • Azamathulla HM (2013) Comments on “Evaluation of selected equations for predicting scour at downstream of ski-jump spillway using laboratory and field data” by Chandan Kumar, P. Sreeja [Engineering Geology 129-130 (2012)]. Engineering Geology 152(1):210–211

    Article  Google Scholar 

  • Azmathulla HM, Deo MC, Deolalikar PB (2005) Neural networks for estimation of scour downstream of a ski-jump bucket. Journal of Hydraulic Engineering, ASCE 131(10):898–908

    Article  Google Scholar 

  • Azamathulla HM, Deo MC, Deolalikar PB (2008a) Alternative neural networks to estimate the scour below spillways. Advances in Engineering Software 38(8):689–698

    Article  Google Scholar 

  • Azamathulla HM, Ghani AA, Zakaria NA, Lai SH, Chang CK, Leow CS (2008b) Genetic Programming to predict ski-jump bucket spillway scour. Journal of Hydro-dynamic 20(4):477–484

    Article  Google Scholar 

  • Azamathulla HM, Ghani AA, Zakaria NA, Guven A (2010) Genetic Programming to Predict Bridge Pier Scour. Journal of Hydraulic Engineering, ASCE 136(3):165–169

    Article  Google Scholar 

  • Azamathulla HM, Guven A, Demir YK (2011) Linear genetic programming to scour below submerged pipeline. Ocean Engineering 38(8–9):995–1000

    Article  Google Scholar 

  • Chee SP, Padiyar PV (1969) Erosion at the base of flip buckets. Canadain Engineering Journal 52(11):22–24

    Google Scholar 

  • Dample PM, Venkatraman CP, Desai SC (1966) Evaluation of scour below ski-jump buckets of spillways. Proceeding of CWPRS Golden Jubilee Symp, Poona, India 1:154–163

    Google Scholar 

  • Eberhart RC, Kennedy J (1995) A new optimizer using particle swarm theory. In: Proc. Sixth International Symposium on Micro Machine and human science, Nagoya, Japan. IEEE Service Center, Piscataway.

  • Farlow SJ (ed) (1984) Self-organizing method in modeling: GMDH type algorithm. Marcel Dekker Inc.

  • Guven A, Azamathulla HM (2012) Gene-expression programming for flip-bucket spillway scour. Water Science & Technology 65(11):1982–1987

    Article  Google Scholar 

  • Gandomi AH, Alavi AH, Mirzahosseini MR, Moghadas NF (2011) Nonlinear Genetic-Based Models for Prediction of Flow Number of Asphalt Mixtures. Journal of Materials in Civil Engineering, ASCE 23(3):248–263

    Article  Google Scholar 

  • Guven A, Azamathulla HM, Zakaria N (2009) Linear genetic programming for prediction of circular piles scour. Ocean Engineering 36:985–991

    Article  Google Scholar 

  • Guven A, Gunal M (2008a) Genetic programming approach for prediction of local scour downstream hydraulic structures. Journal of Irrigation and Drainage Engineering 134(2):241–249

    Article  Google Scholar 

  • Guven A, Gunal M (2008b) Prediction of scour downstream of grade-control structures using neural networks. J Hydraulic En ASCE 134(11):1656–1660

    Article  Google Scholar 

  • Hwang H-S (2006) Fuzzy GMDH-type neural network model and its application to forecasting of mobile communication. Comput Indus Eng 50:450–457

    Google Scholar 

  • Iba H, de Garis H (1996) Extending genetic programming with recombi-native guidance. In: Angeline P, Kinnear K (eds) Advances in Genetic Programming, 2. MIT Press, Cambridge

    Google Scholar 

  • Incyth LHA (1982) Estudio sobre modelo del aliviadero de la Presa Casa de Piedra, Informe Final. DOH-044-03-82, Ezeiza

    Google Scholar 

  • Ivahnenko AG (1971) Polynomial theory of complex systems, IEEE Transactions on Systems, Man, and Cybernetics.

  • Ivakhnenko AG, Ivakhnenko GA (2000) Problems of further development of the group method of data handling algorithms. Part 1. Pattern Recognition and Image Analysis 110:187–194

    Google Scholar 

  • Jamali A, Nariman-Zadeh N, Darvizeh A, Masoumi A, Hamrang S (2009) Multi-objective evolutionary optimization of polynomial neural networks for modelling and prediction of explosive cutting process. Eng Appl Artif Intel 22:676–687

    Google Scholar 

  • Khatsuria RM (2013) Comments on “Evaluation of selected equations for predicting scour at downstream of ski-jump spillway using laboratory and field data” by Chandan Kumar, P. Sreeja [Engineering Geology 129-130 (2012) 98-103]. Engineering Geology 155(4):94–95

    Article  Google Scholar 

  • Kalantary F, Ardalan H, Nariman-Zadeh N (2009) An investigation on the Su-NSPT correlation using GMDH type neural networks and genetic algorithms. Engineering Geology 104(1–2):144–155

    Article  Google Scholar 

  • Koza JR (1992) Genetic Programming: On the Programming of Computers by Means of Natural Selection. The MIT Press, Cambridge

    Google Scholar 

  • Laucelli D, Giustolisi O (2011) Scour depth modelling by a multi-objective evolutionary paradigm. Environmental Modelling & Software 26:498–509

    Article  Google Scholar 

  • Lenzi MA, Comiti F (2003) Local scouring and morphological adjustments in steep channels with check-dam sequences. Geomorphology 55(1–4):97–109

    Article  Google Scholar 

  • Lopardo RA, Lopardo MC, Casado JM (2002) “Local rock scour downstream large dams” Proceeding of International Workshop on Rock Scour Due to High Velocity Jets. Lausanne, Switzerland, pp 55–58

    Google Scholar 

  • Mehrara M, Moeini A, Ahrari M, Erfanifard A (2009) Investigating the efficiency in oil futures market based on GMDH approach. Expert Systems with Applications 36(4):7479–7483

    Article  Google Scholar 

  • Martin RBF (1975) Scouring of rocky river beds by free jet spillways. International Water Power Dam Construction 27(4):152–3

    Google Scholar 

  • Najafzadeh M, Barani GA, Hessami Kermani MR (2013a) Aboutment scour in live-bed and clear-water using GMDH Network. Water Science and Technology 67(5):1121–1128

    Article  Google Scholar 

  • Najafzadeh M, Barani GA, Azamathulla HM (2013b) GMDH to Prediction of Scour Depth around Vertical Piers in Cohesive Soils. Applied Ocean Research 40:35–41

    Article  Google Scholar 

  • Najafzadeh M, Barani GA, Hessami Kermani MR (2013c) GMDH Network Based Back Propagation Algorithm to Predict Abutment Scour in Cohesive Soils. Ocean Engineering 59:100–106

    Article  Google Scholar 

  • Najafzadeh M, Barani GA, Hessami-Kermani MR (2013d) Group Method of Data Handling to Predict Scour Depth around Vertical Piles under regular Waves. Scientia Iranica 20(3):406–413

    Google Scholar 

  • Najafzadeh M, Barani GA (2013) Discussion of “Genetic Programming to Predict River Pipeline Scour” by H. Md. Azamathulla and A. Ab. Ghani. Journal of Pipeline Systems Engineering and Practice, ASCE 4(4):07013001

    Article  Google Scholar 

  • Najafzadeh M, Azamathulla HM (2012) Group Method of Data Handling to Predict Scour Depth Around Bridge Piers. Neural Comput Appl. doi:10.1007/s00521-012-1160-6

    Google Scholar 

  • Najafzadeh M, Barani GA (2011) Comparison of group method of data handling based genetic programming and back propagation systems to predict scour depth around bridge pier. Scientia Iranica 18(6):1207–1213

    Article  Google Scholar 

  • Najafzadeh M, Barani GA, Azamathulla HM (2012) Prediction of pipeline scour depth in clear-water and live-bed conditions using group method of data handling. Neural Computing and Application. doi:10.1007/s00521-012-1258-x

    Google Scholar 

  • Nikolaev NY, Iba H (2003) Polynomial harmonic GMDH learning networks for time series modeling. Neural Networks 16:1527–1540

    Article  Google Scholar 

  • Onwubolu GC (2008) Design of hybrid differential evolution and group method in data handling networks for modeling and prediction. Information Sciences 178:3618–3634

    Article  Google Scholar 

  • Onwubolu GC, Sharma A (2004) Particle swarm optimization for the assignment of facilities to locations. In: New optimization techniques in engineering. Springer, Heidelberg

  • Samadi M, Jabbari E, Azamathulla HM (2012) Assessment of M5′ model tree and classification and regression trees for prediction of scour depth below free overfall spillways. Neural Computing and applications. doi:10.1007/s00521-012-1230-9

    Google Scholar 

  • Sakaguchi A, Yamamoto T (2000) A GMDH network using back propagation and its application to a controller design. Journal of IEEE 4:2691–2697

    Google Scholar 

  • Sanchez E, Shibata T, Zadeh LA (1997) Genetic algorithms and fuzzy logic systems. World Scientific

  • Srinivasan D (2008) Energy demand prediction using GMDH networks. Neuro Computing 72(1–3):625–629

    Google Scholar 

  • Tavakoly Zadeh AA, Kashefipour SM (2009) Modeling local scour on loose bed downstream of grade-control structures using artificial neural network. Journal of Applied Science 8(11):2067–2074

    Google Scholar 

  • Veronese A (1937) Erosion de Fondoa Valle diuno Scarico. Annali dei Lavori Publicci 759:717–726

    Google Scholar 

  • Witczak M, Korbicz J, Mrugalski M, Patton R (2006) A GMDH neural network -based approach to robust fault diagnosis: Application to the DAMADICS benchmark problem. Control Engineering Practice 14(6):671–683

    Article  Google Scholar 

  • Wu CM (1973) Scour at downstream end of dams in Taiwan. International symposium on river mechanics, Bangkok, Thailand I, A 13, 1–6

  • Yang XS, Gandomi AH, Talatahari S, Alavi AH (2013) Metaheuristics in Water Resources, Geotechnical and Transportation Engineering, vol 2. Elsevier, Waltham, p 496

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Shahid Bahonar University of Kerman, P.O. BOX 76169133, Kerman, Iran

    Mohammad Najafzadeh, Gholam-Abbas Barani & Masoud-Reza Hessami-Kermani

Authors
  1. Mohammad Najafzadeh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Gholam-Abbas Barani
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Masoud-Reza Hessami-Kermani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mohammad Najafzadeh.

Additional information

Communicated by: H. A. Babaie

Appendices

Appendix A. Selective polynomials of the GMDH-PSO and GMDH-GP networks for predicting the d s /d w

Selective polynomial neurons of the GMDH-PSO were represented as follows:

$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_1^1=1+0.5296\left(q/\sqrt{g.}{d}_w^3\right)+0.2929\left(H/{d}_w\right)+0.31627\left(q/\sqrt{g.}{d}_w^3\right)\left(H/{d}_w\right)\hfill \\ {}+0.2775{\left(H/{d}_w\right)}^2-0.03919{\left(q/\sqrt{q.}{d}_w^3\right)}^2\hfill \end{array} $$
(41)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_5^1=-0.734+0.4496\left(q/\sqrt{g.}{d}_w^3\right)+0.896\left(R/{d}_w\right)-0.056\left(q/\sqrt{g.}{d}_w^3\right)\left(R/{d}_w\right)\hfill \\ {}+0.061{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.0238{\left(R/{d}_w\right)}^2\hfill \end{array} $$
(42)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_8^1=1+\left(q/\sqrt{g.}{d}_w^3\right)+\left({d}_{50}/{d}_w\right)+0.9903\left(q/\sqrt{g.}{d}_w^3\right)\left({d}_{50}/{d}_w\right)\hfill \\ {}-0.0925{\left({d}_{50}/{d}_w\right)}^2+0.47166{\left(q/\sqrt{g.}{d}_w^3\right)}^2\hfill \end{array} $$
(43)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_{10}^1=1+0.1841\left(q/\sqrt{g.}{d}_w^3\right)+0.11955\left(\varphi \right)-0.7924\left(q/\sqrt{g.}{d}_w^3\right)\left(\varphi \right)\hfill \\ {}+0.36708{\left(q/\sqrt{g.}{d}_w^3\right)}^2+0.2586{\left(\varphi \right)}^2\hfill \end{array} $$
(44)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_2^2=0.299+{\left({d}_s/{d}_w\right)}_1^1-0.0607{\left({d}_s/{d}_w\right)}_8^1-0.2573{\left({d}_s/{d}_w\right)}_1^1{\left({d}_s/{d}_w\right)}_8^1\hfill \\ {}+0.12091{\left({\left({d}_s/{d}_w\right)}_1^1\right)}^2+0.10617{\left({\left({d}_s/{d}_w\right)}_8^1\right)}^2\hfill \end{array} $$
(45)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_3^2=-0.0899+0.59299{\left({d}_s/{d}_w\right)}_3^1+0.4347{\left({d}_s/{d}_w\right)}_9^1+0.0839{\left({d}_s/{d}_w\right)}_3^1{\left({d}_s/{d}_w\right)}_9^1\hfill \\ {}-0.03295{\left({\left({d}_s/{d}_w\right)}_3^1\right)}^2-0.0472{\left({\left({d}_s/{d}_w\right)}_9^1\right)}^2\hfill \end{array} $$
(46)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_6^2=-0.5+0.24131{\left({d}_s/{d}_w\right)}_8^1+0.93{\left({d}_s/{d}_w\right)}_{10}^1+0.1845{\left({d}_s/{d}_w\right)}_8^1{\left({d}_s/{d}_w\right)}_{10}^1\hfill \\ {}-0.241{\left({\left({d}_s/{d}_w\right)}_8^1\right)}^2+0.06898{\left({\left({d}_s/{d}_w\right)}_{10}^1\right)}^2\hfill \end{array} $$
(47)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_1^3=0.4067+0.408{\left({d}_s/{d}_w\right)}_2^2+0.7757{\left({d}_s/{d}_w\right)}_3^2-0.1232{\left({d}_s/{d}_w\right)}_2^2{\left({d}_s/{d}_w\right)}_3^2\hfill \\ {}+0.07767{\left({\left({d}_s/{d}_w\right)}_2^2\right)}^2+0.0112{\left({\left({d}_s/{d}_w\right)}_3^2\right)}^2\hfill \end{array} $$
(48)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_2^3=-0.7601+0.0238{\left({d}_s/{d}_w\right)}_2^2+{\left({d}_s/{d}_w\right)}_6^2+0.3503{\left({d}_s/{d}_w\right)}_2^2{\left({d}_s/{d}_w\right)}_6^2\hfill \\ {}+0.1167{\left({\left({d}_s/{d}_w\right)}_2^2\right)}^2-0.2033{\left({\left({d}_s/{d}_w\right)}_6^2\right)}^2\hfill \end{array} $$
(49)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_1^4=0.3317-0.0681{\left({d}_s/{d}_w\right)}_1^3+0.7588{\left({d}_s/{d}_w\right)}_2^3-0.61847{\left({d}_s/{d}_w\right)}_1^3{\left({d}_s/{d}_w\right)}_2^3\hfill \\ {}-0.2927{\left({\left({d}_s/{d}_w\right)}_1^3\right)}^2+0.35601{\left({\left({d}_s/{d}_w\right)}_2^3\right)}^2\hfill \end{array} $$
(50)

Structure of the proposed GMDH-PSO network for predicting the d s /d w was represented as:

figure a

Fig. 8 Improved structure of the GMDH-BP network for predicting the d s /d w

and for the GMDH-GP:

$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_4^1= GP\left(q/\sqrt{g.{d}_w^3},{d}_{50}/{d}_w\right)=0.3313-9344\left(-4.289810+q/\sqrt{g.{d}_w^3}\right)\left(q/\sqrt{g.{d}_w^3}\right)\hfill \\ {}-3.166\left(q/\sqrt{g.{d}_w^3}\right)\left({d}_{50}/{d}_w\right)\left(-\left(q/\sqrt{g.{d}_w^3}\right)+{d}_{50}/{d}_w\right)\hfill \end{array} $$
(51)
$$ {\left({d}_s/{d}_w\right)}_5^1= GP\left(q/\sqrt{g.{d}_w^3},R/{d}_w\right)=0.7-0.5304\left(R/{d}_w\right)-0.5304{\left(q/\sqrt{g.{d}_w^3}\right)}^2+5.685\left(q/\sqrt{g.{d}_w^3}\right) $$
(52)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_{10}^1= GP\left(q/\sqrt{g.}{d}_w^3,\varphi \right)=-0.17-1.614{\left(q/\sqrt{g.}{d}_w^3\right)}^2{\left(\varphi \right)}^2\hfill \\ {}+\left(0.7924-\left(\varphi \right)\right)\left(q/\sqrt{g.}{d}_w^3\right)\hfill \end{array} $$
(53)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_1^2= GP\left({\left({d}_s/{d}_w\right)}_4^1,{\left({d}_s/{d}_w\right)}_5^1\right)=0.422+0.1305{\left({d}_s/{d}_w\right)}_4^1{\left({d}_s/{d}_w\right)}_5^1-0.08619{\left({\left({d}_s/{d}_w\right)}_4^1\right)}^2\hfill \\ {}+0.4232{\left({d}_s/{d}_w\right)}_4^1+0.2532{\left({d}_s/{d}_w\right)}_5^1\hfill \end{array} $$
(54)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_2^2= GP\left({\left({d}_s/{d}_w\right)}_4^1,{\left({d}_s/{d}_w\right)}_{10}^1\right)=1.277-0.2366{\left({d}_s/{d}_w\right)}_4^1+0.2366{\left({d}_s/{d}_w\right)}_{10}^1\hfill \\ {}+0.186\left({\left({d}_s/{d}_w\right)}_4^1{\left({d}_s/{d}_w\right)}_{10}^1-0.0087{\left({\left({d}_s/{d}_w\right)}_4^1\right)}^2{\left({d}_s/{d}_w\right)}_{10}^1\right)\hfill \end{array} $$
(55)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_1^3= GP\left({\left({d}_s/{d}_w\right)}_1^2,{\left({d}_s/{d}_w\right)}_2^2\right)=-0.451+0.4635{\left({d}_s/{d}_w\right)}_1^2{\left({d}_s/{d}_w\right)}_2^2\hfill \\ {}+1.28{\left({d}_s/{d}_w\right)}_2^2-0.4913{\left({\left({d}_s/{d}_w\right)}_2^2\right)}^2\hfill \end{array} $$
(56)

Structure of the proposed GMDH-GP network for predicting the d s /d w was represented as:

figure b

Fig. 9 Improved structure of the GMDH-GP network for predicting the d s /d w

Appendix. B. Selective polynomials of the alternative GMDH networks for predicting the l s /d w

Selective polynomial neurons of the GMDH-BP were proposed as follows:

$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^1=0.2663+0.7866\left(q/\sqrt{g.}{d}_w^3\right)+0.181\left(H/{d}_w\right)+0.2064\left(q/\sqrt{g.}{d}_w^3\right)\left(H/{d}_w\right)\hfill \\ {}-0.111{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.0939{\left(H/{d}_w\right)}^2\hfill \end{array} $$
(57)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_5^1=1.2928+1.579\left(q/\sqrt{g.}{d}_w^3\right)-0.7217\left(R/{d}_w\right)+0.893\left(q/\sqrt{g.}{d}_w^3\right)\left(R/{d}_w\right)\hfill \\ {}-0.4553{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.4338{\left(R/{d}_w\right)}^2\hfill \end{array} $$
(58)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_8^1=4.789+10.6187\left(q/\sqrt{g.}{d}_w^3\right)-24.796\left({d}_{50}/{d}_w\right)-4.884\left(q/\sqrt{g.}{d}_w^3\right)\left({d}_{50}/{d}_w\right)\hfill \\ {}-0.8731{\left(q/\sqrt{g.}{d}_w^3\right)}^2+127.013{\left({d}_{50}/{d}_w\right)}^2\hfill \end{array} $$
(59)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_{10}^1=0.8662+1.494\left(q/\sqrt{g.}{d}_w^3\right)-0.5758\left(\varphi \right)-0.7969\left(q/\sqrt{g.}{d}_w^3\right)\left(\varphi \right)\hfill \\ {}-0.4048{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.3898{\left(\varphi \right)}^2\hfill \end{array} $$
(60)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^2=0.2663+0.7865{\left({l}_s/{d}_w\right)}_1^1+0.18098{\left({l}_s/{d}_w\right)}_5^1+0.2064{\left({l}_s/{d}_w\right)}_1^1{\left({l}_s/{d}_w\right)}_5^1\hfill \\ {}-0.11136{\left({\left({l}_s/{d}_w\right)}_1^1\right)}^2-0.09398{\left({\left({l}_s/{d}_w\right)}_5^1\right)}^2\hfill \end{array} $$
(61)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_2^2=1.2928+1.5797{\left({l}_s/{d}_w\right)}_1^1-0.72179{\left({l}_s/{d}_w\right)}_8^1+0.8929{\left({l}_s/{d}_w\right)}_3^1{\left({l}_s/{d}_w\right)}_8^1\hfill \\ {}-0.45531{\left({\left({l}_s/{d}_w\right)}_1^1\right)}^2-0.43386{\left({\left({l}_s/{d}_w\right)}_8^1\right)}^2\hfill \end{array} $$
(62)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_3^2=0.86624+1.4941{\left({l}_s/{d}_w\right)}_1^1-0.578{\left({l}_s/{d}_w\right)}_{10}^1+0.7969{\left({l}_s/{d}_w\right)}_1^1{\left({l}_s/{d}_w\right)}_{10}^1\hfill \\ {}-0.40489{\left({\left({l}_s/{d}_w\right)}_1^1\right)}^2-0.3898{\left({\left({l}_s/{d}_w\right)}_{10}^1\right)}^2\hfill \end{array} $$
(63)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^3=0.14835+0.50484{\left({l}_s/{d}_w\right)}_1^2+0.49762{\left({l}_s/{d}_w\right)}_2^2+1.03938{\left({l}_s/{d}_w\right)}_1^2{\left({l}_s/{d}_w\right)}_2^2\hfill \\ {}-0.52389{\left({\left({l}_s/{d}_w\right)}_1^2\right)}^2-0.5155{\left({\left({l}_s/{d}_w\right)}_2^2\right)}^2\hfill \end{array} $$
(64)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_2^3=0.04938+1.0437{\left({l}_s/{d}_w\right)}_1^2-0.035138{\left({l}_s/{d}_w\right)}_3^2+0.87513{\left({l}_s/{d}_w\right)}_1^2{\left({l}_s/{d}_w\right)}_3^2\hfill \\ {}-0.45887{\left({\left({l}_s/{d}_w\right)}_1^2\right)}^2-0.41646{\left({\left({l}_s/{d}_w\right)}_3^2\right)}^2\hfill \end{array} $$
(65)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^4=-0.0517-1.0069{\left({l}_s/{d}_w\right)}_1^3+2.0254{\left({l}_s/{d}_w\right)}_2^3+2.552{\left({l}_s/{d}_w\right)}_1^3{\left({l}_s/{d}_w\right)}_2^3\hfill \\ {}-1.239{\left({\left({l}_s/{d}_w\right)}_1^3\right)}^2-1.31311{\left({\left({l}_s/{d}_w\right)}_2^3\right)}^2\hfill \end{array} $$
(66)

Furthermore, structure of the proposed GMDH-PSO network for predicting the l s /d w was represented as:

figure c

Fig. 10 Improved structure of the GMDH-BP network for predicting the l s /d w

Selective polynomial neurons of the GMDH-PSO were given as follows:

$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^1=0.9403+\left(q/\sqrt{g.}{d}_w^3\right)+0.3255\left(H/{d}_w\right)+0.4097\left(q/\sqrt{g.}{d}_w^3\right)\left(H/{d}_w\right)\hfill \\ {}-0.01{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.01{\left(H/{d}_w\right)}^2\hfill \end{array} $$
(67)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_6^1=0.9869+\left(H/{d}_w\right)+\left({d}_{50}/{d}_w\right)+0.9996\left(H/{d}_w\right)\left({d}_{50}/{d}_w\right)\hfill \\ {}-0.000631{\left(H/{d}_w\right)}^2+0.47166{\left({d}_{50}/{d}_w\right)}^2\hfill \end{array} $$
(68)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_9^1=1+0.94703\left(H/{d}_w\right)+0.9348\left(\varphi \right)+0.79233\left(H/{d}_w\right)\left(\varphi \right)\\ {}-0.01{\left(H/{d}_w\right)}^2+0.82577{\left(\varphi \right)}^2\end{array} $$
(69)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_2^2=0.8006+0.43532{\left({l}_s/{d}_w\right)}_1^1+0.11991{\left({l}_s/{d}_w\right)}_6^1-0.01{\left({l}_s/{d}_w\right)}_1^1{\left({l}_s/{d}_w\right)}_6^1\\ {}-0.01{\left({\left({l}_s/{d}_w\right)}_1^1\right)}^2+0.0503{\left({\left({l}_s/{d}_w\right)}_6^1\right)}^2\end{array} $$
(70)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_3^2=0.3843+0.9528{\left({l}_s/{d}_w\right)}_1^1+0.70082{\left({l}_s/{d}_w\right)}_9^1-0.01{\left({l}_s/{d}_w\right)}_1^1{\left({l}_s/{d}_w\right)}_9^1\hfill \\ {}-0.00457{\left({\left({l}_s/{d}_w\right)}_1^1\right)}^2-0.01{\left({\left({l}_s/{d}_w\right)}_9^1\right)}^2\hfill \end{array} $$
(71)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_6^2=1-0.01{\left({l}_s/{d}_w\right)}_6^1+0.86967{\left({l}_s/{d}_w\right)}_9^1-0.01{\left({l}_s/{d}_w\right)}_6^1{\left({l}_s/{d}_w\right)}_9^1\hfill \\ {}0.02381{\left({\left({l}_s/{d}_w\right)}_6^1\right)}^2-0.00943{\left({\left({l}_s/{d}_w\right)}_9^1\right)}^2\hfill \end{array} $$
(72)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^3=0.080334+0.03444{\left({l}_s/{d}_w\right)}_2^2+{\left({l}_s/{d}_w\right)}_3^2+0.02277{\left({l}_s/{d}_w\right)}_2^2{\left({l}_s/{d}_w\right)}_3^2\hfill \\ {}-0.01{\left({\left({l}_s/{d}_w\right)}_2^2\right)}^2-0.01{\left({\left({l}_s/{d}_w\right)}_3^2\right)}^2\hfill \end{array} $$
(73)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_2^3=-0.01+{\left({l}_s/{d}_w\right)}_2^2+0.471835{\left({l}_s/{d}_w\right)}_6^2-0.01{\left({l}_s/{d}_w\right)}_2^2{\left({l}_s/{d}_w\right)}_6^2\hfill \\ {}-0.01{\left({\left({l}_s/{d}_w\right)}_2^2\right)}^2+0.004188{\left({\left({l}_s/{d}_w\right)}_6^2\right)}^2\hfill \end{array} $$
(74)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_1^4=0.40802+0.4203{\left({l}_s/{d}_w\right)}_1^3+0.38145{\left({l}_s/{d}_w\right)}_2^3-0.01{\left({l}_s/{d}_w\right)}_1^3{\left({l}_s/{d}_w\right)}_2^3\hfill \\ {}-0.02779{\left({\left({l}_s/{d}_w\right)}_1^3\right)}^2-0.01{\left({\left({l}_s/{d}_w\right)}_2^3\right)}^2\hfill \end{array} $$
(75)

Structure of the proposed GMDH-BP network for predicting the l s /d w was represented as:

figure d

Fig. 11 Improved structure of the GMDH-BP network for predicting the l s /d w

and for the proposed GMDH-GP model:

$$ {\left({l}_s/{d}_w\right)}_1^1= GP\left(q/\sqrt{g.{d}_w^3},H/{d}_w\right)=3.7-0.9857{\left(q/\sqrt{g.{d}_w^3}\right)}^2+10.9\left(q/\sqrt{g.{d}_w^3}\right) $$
(76)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_8^1= GP\left(q/\sqrt{g.{d}_w^3},{d}_{50}/{d}_w\right)=4+10.77\left(q/\sqrt{g.{d}_w^3}\right)+10.77{\left({d}_{50}/{d}_w\right)}^2-0.9738{\left(q/\sqrt{g.{d}_w^3}\right)}^2\hfill \\ {}-0.01{\left({d}_{50}/{d}_w\right)}^2\hfill \end{array} $$
(77)
$$ \begin{array}{l}{\left({l}_s/{d}_w\right)}_{10}^1= GP\left(q/\sqrt{g.{d}_w^3},\varphi \right)=1.928+11.63\left(q/\sqrt{g.{d}_w^3}\right)+5.518{\left(\varphi \right)}^2-1.004\left(\varphi \right)\left(q/\sqrt{g.{d}_w^3}\right)\hfill \\ {}-1.004{\left(q/\sqrt{g.{d}_w^3}\right)}^2\hfill \end{array} $$
(78)
$$ {\left({l}_s/{d}_w\right)}_2^2= GP\left({\left({l}_s/{d}_w\right)}_1^1,{\left({l}_s/{d}_w\right)}_{10}^1\right)=-1.201-0.0504{\left({l}_s/{d}_w\right)}_1^1{\left({l}_s/{d}_w\right)}_{10}^1+0.04463{\left({\left({l}_s/{d}_w\right)}_{10}^1\right)}^2+1.188{\left({l}_s/{d}_w\right)}_{10}^1 $$
(79)
$$ {\left({l}_s/{d}_w\right)}_3^2= GP\left({\left({l}_s/{d}_w\right)}_8^1,{\left({l}_s/{d}_w\right)}_{10}^1\right)=-0.99+1.198{\left({l}_s/{d}_w\right)}_{10}^1-0.004518{\left({\left({l}_s/{d}_w\right)}_{10}^1\right)}^2-0.04441{\left({l}_s/{d}_w\right)}_8^1 $$
(80)
$$ {\left({l}_s/{d}_w\right)}_1^3= GP\left({\left({l}_s/{d}_w\right)}_2^2,{\left({l}_s/{d}_w\right)}_3^2\right)=0.07471+1.497{\left({l}_s/{d}_w\right)}_2^2-0.4991{\left({l}_s/{d}_w\right)}_3^2+1.826{\left({\left({l}_s/{d}_w\right)}_2^2-{\left({l}_s/{d}_w\right)}_3^2\right)}^2 $$
(81)

Structure of the proposed GMDH-GP network for predicting the l s /d w was represented as:

figure e

Fig. 12 Improved structure of the GMDH-GP network for predicting the l s /d w

Appendix C. Selective polynomials of the alternative GMDH networks for predicting the w s /d w

Selective polynomial neurons of the GMDH-BP can be expressed as follows:

$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^1=3.0059+7.4598\left(q/\sqrt{g.}{d}_w^3\right)+0.24244\left(H/{d}_w\right)-0.07705\left(q/\sqrt{g.}{d}_w^3\right)\left(H/{d}_w\right)\hfill \\ {}-0.6064{\left(q/\sqrt{g.}{d}_w^3\right)}^2+0.02356{\left(H/{d}_w\right)}^2\hfill \end{array} $$
(82)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_3^1=0.59015+2.518\left(R/{d}_w\right)+32.0963\left({d}_{50}/{d}_w\right)-10.2989\left(R/{d}_w\right)\left({d}_{50}/{d}_w\right)\hfill \\ {}+0.005464{\left(R/{d}_w\right)}^2+164.6615{\left({d}_{50}/{d}_w\right)}^2\hfill \end{array} $$
(83)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_6^1=2.0569+0.5275\left(H/{d}_w\right)+49.523\left({d}_{50}/{d}_w\right)+8.3201\left(H/{d}_w\right)\left({d}_{50}/{d}_w\right)\hfill \\ {}+0.007203{\left(H/{d}_w\right)}^2-399.941{\left({d}_{50}/{d}_w\right)}^2\hfill \end{array} $$
(84)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_9^1=-52.8145+5.5315\left(H/{d}_w\right)+168.467\left(\varphi \right)-7.996\left(H/{d}_w\right)\left(\varphi \right)\hfill \\ {}+0.01805{\left(H/{d}_w\right)}^2-121.9274{\left(\varphi \right)}^2\hfill \end{array} $$
(85)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^2=-1.09644+0.368036{\left({w}_s/{d}_w\right)}_1^1+0.74573{\left({w}_s/{d}_w\right)}_3^1-0.07171{\left({w}_s/{d}_w\right)}_1^1{\left({w}_s/{d}_w\right)}_3^1\hfill \\ {}+0.037116{\left({\left({w}_s/{d}_w\right)}_1^1\right)}^2+0.031346{\left({\left({w}_s/{d}_w\right)}_3^1\right)}^2\hfill \end{array} $$
(86)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_2^2=-0.23395-0.08297{\left({w}_s/{d}_w\right)}_1^1+1.0433{\left({w}_s/{d}_w\right)}_6^1-0.3297{\left({w}_s/{d}_w\right)}_1^1{\left({w}_s/{d}_w\right)}_6^1\hfill \\ {}+0.16358{\left({\left({w}_s/{d}_w\right)}_1^1\right)}^2+0.16695{\left({\left({w}_s/{d}_w\right)}_6^1\right)}^2\hfill \end{array} $$
(87)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_5^2=0.6848+0.53005{\left({d}_s/{d}_w\right)}_3^1+0.37741{\left({d}_s/{d}_w\right)}_9^1+0.09447{\left({d}_s/{d}_w\right)}_3^1{\left({d}_s/{d}_w\right)}_9^1\hfill \\ {}-0.055287{\left({\left({d}_s/{d}_w\right)}_3^1\right)}^2-0.034938{\left({\left({d}_s/{d}_w\right)}_9^1\right)}^2\hfill \end{array} $$
(88)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_2^3=0.51324-0.15495{\left({w}_s/{d}_w\right)}_1^2+1.160389{\left({w}_s/{d}_w\right)}_5^2+0.347713{\left({w}_s/{d}_w\right)}_1^2{\left({w}_s/{d}_w\right)}_5^2\hfill \\ {}-0.15086{\left({\left({w}_s/{d}_w\right)}_1^2\right)}^2-0.197052{\left({\left({w}_s/{d}_w\right)}_5^2\right)}^2\hfill \end{array} $$
(89)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_3^3=0.15692+0.086079{\left({w}_s/{d}_w\right)}_2^2+0.930205{\left({w}_s/{d}_w\right)}_5^2+0.25362{\left({w}_s/{d}_w\right)}_2^2{\left({w}_s/{d}_w\right)}_5^2\hfill \\ {}-0.104692{\left({\left({w}_s/{d}_w\right)}_2^2\right)}^2-0.14929{\left({\left({w}_s/{d}_w\right)}_5^2\right)}^2\hfill \end{array} $$
(90)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^4=-0.88519+1.06243{\left({w}_s/{d}_w\right)}_2^3+0.043505{\left({w}_s/{d}_w\right)}_3^3-1.09344{\left({w}_s/{d}_w\right)}_2^3{\left({w}_s/{d}_w\right)}_3^3\hfill \\ {}+0.53076{\left({\left({w}_s/{d}_w\right)}_2^3\right)}^2+0.558807{\left({\left({w}_s/{d}_w\right)}_3^3\right)}^2\hfill \end{array} $$
(100)

Also, structure of the proposed GMDH-BP network for predicting the w s /d w was represented as:

figure f

Fig. 13 Improved structure of the GMDH-BP network for predicting the w s /d w

Selective polynomial neurons of the GMDH-BP can be expressed as follows:

$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^1=-0.75-0.50385\left(q/\sqrt{g.}{d}_w^3\right)+1.7409\left(H/{d}_w\right)+0.33616\left(q/\sqrt{g.}{d}_w^3\right)\left(H/{d}_w\right)\hfill \\ {}-0.17057{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.04425{\left(H/{d}_w\right)}^2\hfill \end{array} $$
(101)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_8^1=2+2\left(q/\sqrt{g.}{d}_w^3\right)+1.3846\left({d}_{50}/{d}_w\right)+2\left(q/\sqrt{g.}{d}_w^3\right)\left({d}_{50}/{d}_w\right)\hfill \\ {}+0.126398{\left(q/\sqrt{g.}{d}_w^3\right)}^2-0.124435{\left({d}_{50}/{d}_w\right)}^2\hfill \end{array} $$
(102)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_{10}^1=2+2\left(q/\sqrt{g.}{d}_w^3\right)+2\left(\varphi \right)+1.2215\left(q/\sqrt{g.}{d}_w^3\right)\left(\varphi \right)\hfill \\ {}+0.08696{\left(q/\sqrt{g.}{d}_w^3\right)}^2+0.62547{\left(\varphi \right)}^2\hfill \end{array} $$
(103)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_2^2=0.16324+1.290411{\left({w}_s/{d}_w\right)}_1^1+0.783622{\left({w}_s/{d}_w\right)}_8^1+0.313924{\left({w}_s/{d}_w\right)}_1^1{\left({w}_s/{d}_w\right)}_8^1\hfill \\ {}-0.09234{\left({\left({w}_s/{d}_w\right)}_1^1\right)}^2-0.13886{\left({\left({w}_s/{d}_w\right)}_8^1\right)}^2\hfill \end{array} $$
(104)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_3^2=1.13187+0.55885{\left({w}_s/{d}_w\right)}_3^1+1.6008{\left({w}_s/{d}_w\right)}_9^1+0.4028{\left({w}_s/{d}_w\right)}_3^1{\left({w}_s/{d}_w\right)}_9^1\hfill \\ {}-0.12526{\left({\left({w}_s/{d}_w\right)}_3^1\right)}^2-0.19329{\left({\left({w}_s/{d}_w\right)}_9^1\right)}^2\hfill \end{array} $$
(105)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_6^2=0.48605+0.16088{\left({d}_s/{d}_w\right)}_8^1+0.17249{\left({d}_s/{d}_w\right)}_{10}^1+0.85044{\left({d}_s/{d}_w\right)}_8^1{\left({d}_s/{d}_w\right)}_{10}^1\hfill \\ {}-0.75{\left({\left({d}_s/{d}_w\right)}_8^1\right)}^2-0.083213{\left({\left({d}_s/{d}_w\right)}_{10}^1\right)}^2\hfill \end{array} $$
(106)
$$ \begin{array}{l}{\left({d}_s/{d}_w\right)}_1^3=0.13941+0.35861{\left({d}_s/{d}_w\right)}_2^2+10668{\left({d}_s/{d}_w\right)}_3^2+0.22018{\left({d}_s/{d}_w\right)}_2^2{\left({d}_s/{d}_w\right)}_3^2\hfill \\ {}+0.05174{\left({\left({d}_s/{d}_w\right)}_2^2\right)}^2-0.31643{\left({\left({d}_s/{d}_w\right)}_3^2\right)}^2\hfill \end{array} $$
(107)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_2^3=-0.74774+1.41079{\left({w}_s/{d}_w\right)}_2^2+0.64573{\left({w}_s/{d}_w\right)}_6^2+0.028514{\left({w}_s/{d}_w\right)}_2^2{\left({w}_s/{d}_w\right)}_6^2\hfill \\ {}-0.02972{\left({\left({w}_s/{d}_w\right)}_2^2\right)}^2-0.015677{\left({\left({w}_s/{d}_w\right)}_6^2\right)}^2\hfill \end{array} $$
(108)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^4=-0.390901-0.38199{\left({w}_s/{d}_w\right)}_1^3+0.575127{\left({w}_s/{d}_w\right)}_2^3+0.015529{\left({w}_s/{d}_w\right)}_1^3{\left({w}_s/{d}_w\right)}_2^3\hfill \\ {}+0.003{\left({\left({w}_s/{d}_w\right)}_1^3\right)}^2-0.0006342{\left({\left({w}_s/{d}_w\right)}_2^3\right)}^2\hfill \end{array} $$
(109)

Structure of the proposed GMDH-PSO network for predicting the w s /d w was represented as:

figure g

Fig. 14 Improved structure of the GMDH-PSO network for predicting the w s /d w

and for the proposed GMDH-GP model:

$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^1= GP\left(q/\sqrt{g.{d}_w^3},H/{d}_w\right)=5.976+0.1422{\left(q/\sqrt{g.{d}_w^3}\right)}^3+\left(-0.9703-\left(H/{d}_w\right)\right){\left(q/\sqrt{g.{d}_w^3}\right)}^2\hfill \\ {}+1.034\left(R/{d}_w\right)\left(q/\sqrt{g.{d}_w^3}\right)\hfill \end{array} $$
(110)
$$ {\left({w}_s/{d}_w\right)}_6^1= GP\left(H/{d}_w,{d}_{50}/{d}_w\right)=2.207+0.4485\left(H/{d}_w\right)+0.02278{\left(H/{d}_w\right)}^2+36.86\left({d}_{50}/{d}_w\right) $$
(111)
$$ {\left({w}_s/{d}_w\right)}_9^1= GP\left(H/{d}_w,\varphi \right)=4.084+\left(0.7502\varphi -1.178{\varphi}^2\right){\left(H/{d}_w\right)}^2+1.072\left(H/{d}_w\right)\varphi $$
(112)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^2= GP\left({\left({w}_s/{d}_w\right)}_1^1,{\left({w}_s/{d}_w\right)}_6^1\right)=-0.1871+0.7347{\left({w}_s/{d}_w\right)}_6^1+0.2449{\left({w}_s/{d}_w\right)}_1^1\hfill \\ {}+0.1298{\left({\left({w}_s/{d}_w\right)}_1^1-{\left({w}_s/{d}_w\right)}_6^1\right)}^2\hfill \end{array} $$
(113)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_3^2= GP\left({\left({w}_s/{d}_w\right)}_6^1,{\left({w}_s/{d}_w\right)}_9^1\right)=0.04935+0.05274\left({\left({w}_s/{d}_w\right)}_6^1-{\left({w}_s/{d}_w\right)}_9^1\right)\left({\left({w}_s/{d}_w\right)}_9^1\right)\hfill \\ {}+0.91{\left({w}_s/{d}_w\right)}_9^1+0.09064{\left({w}_s/{d}_w\right)}_6^1\hfill \end{array} $$
(114)
$$ \begin{array}{l}{\left({w}_s/{d}_w\right)}_1^3= GP\left({\left({w}_s/{d}_w\right)}_1^2,{\left({w}_s/{d}_w\right)}_3^2\right)=0.059+0.9439{\left({w}_s/{d}_w\right)}_3^2+0.05653{\left({w}_s/{d}_w\right)}_1^2\hfill \\ {}+0.05534{\left({w}_s/{d}_w\right)}_2^2{\left({w}_s/{d}_w\right)}_3^2-0.05534{\left({\left({w}_s/{d}_w\right)}_3^2\right)}^2\hfill \end{array} $$
(115)

Structure of the proposed GMDH-GP network for predicting the w s /d w was represented as:

figure h

Fig. 15 Improved structure of the GMDH-GP network for predicting the w s /d w

Rights and permissions

Reprints and permissions

About this article

Cite this article

Najafzadeh, M., Barani, GA. & Hessami-Kermani, MR. Group Method of Data Handling to Predict Scour at Downstream of a Ski-Jump Bucket Spillway. Earth Sci Inform 7, 231–248 (2014). https://doi.org/10.1007/s12145-013-0140-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12145-013-0140-4

Keywords