Abstract
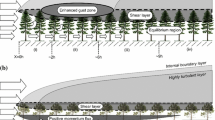
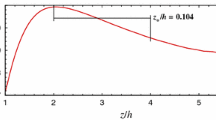
Leaf area index(LAI) of forest is the sum of vertical projection area of plant leaves per unit area. Stand density refers to the number of trees per unit area. These two parameters are important indexes to characterize the wind resistance effect of forest underlying surface. This paper presents a theoretical model of the flow field above a forest canopy layer and the variation of forest aerodynamic roughness (Z0), zero-plane displacement (d), and friction speed (U *) with stand density and leaf area index (LAI) were investigated. The results show that stand density does not affect the variation of Z0, d, or u* with LAI. The aerodynamic roughness first increases and then decreases with increasing LAI, and the ratio of roughness to forest height Z0/h is below 0.16. The value of d increases to a maximum with increasing of LAI and then remains stable. Moreover, the maximum value increases with increasing stand density. The maximum d/h ratios corresponding to stand densities of 400 ha−1, 1000 ha−1 and 1600 ha−1 were 0.68, 0.88, and 0.93, respectively. Friction speed decreased with increasing LAI, then tends to become stable. The minimum friction speed decreases with increasing stand density and the minimum values of u* corresponding to stand densities of 400 ha−1, 1000 ha−1, and 1600 ha−1 were 0.65, 0.48, and 0.44, respectively. At the minimum friction velocity, the corresponding LAI was found to increase with increasing stand density.









Similar content being viewed by others
References
Bingöl F (2019) A simplified method on estimation of forest roughness by use of aerial LIDAR data. Energy Sci Eng 7(6):3274–3282
Choudhury BJ, Monteith JL (1988) A four layer model for the heat budget of homogeneous land surfaces. Q J R Meteorol Soc 114(480):373–398
Cowan IR (1968) Mass, heat and momentum exchange between stands of plants and their atmospheric environment. Q J R Meteorol Soc 94(402):523–544
Dalpé B, Masson C (2009) Numerical simulation of wind flow near a forest edge. J WindEng Aerodyn 97(5–6):228–241
Garratt JR (1994) Review: the atmospheric boundary layer. Earth-Sci Rev 37(1–2):89–134
Katul GG, Mahrt L, Poggi D et al (2004) One- and two-equation models for canopy turbulence. Bound Layer Meteorol 113(1):81–109
Krogstad P-Ã, Andersson HI, Bakken OM et al (2005) An experimental and numerical study of channel flow with rough walls. J Fluid Mech 530(1):327–352
Liu J, Chen JM, Black TA et al (1996) k-ε modelling of turbulent air flow downwind of a model forest edge. Bound Layer Meteorol 77(1):21–44
Massman WJ, Weil JC (1999) An analytical one-dimensional second-order closure model of turbulence statistics and the Lagrangian time scale within and above plant canopies of arbitrary structure. Bound Layer Meteorol 91(1):81–107
Minvielle F, Marticorena B, Gillette DA et al (2003) Relationship between the aerodynamic roughness length and the roughness density in cases of low roughness density. Environ Fluid Mech 3(3):249–267
Nakai T, Sumida A, Daikoku K et al (2008) Parameterisation of aerodynamic roughness over boreal, cool-and warm-temperate forests. Agric For Meteorol 148(12):1916–1925
Raupach MR, Shaw RH (1982) Averaging procedures for flow within vegetation canopies. Bound Layer Meteorol 22(1):79–90
Salleh Mohd MR, Abdul Rahman MZ, Abu Bakar MA et al (2016) Estimation of aerodynamic roughness and zero plane displacement using medium density of airborne LIDAR data. Int Arch Photogramm Remote Sens Spat Inf Sci 42:217–224
Sanz C (2003) A Note on k-ε modelling of vegetation canopy air-flows. Bound-Layer Meteorol 108(1):191–197
Shao Y, Yang Y (2005) scheme for drag partition over rough surfaces. Atmos Environ 39(38):7351–7361
Silva Lopes A, Palma JMLM, Piomelli U (2015) On the determination of effective aerodynamic roughness of surfaces with vegetation patches. Bound Layer Meteorol 156(1):113–130
Tanner CB, Pelton WL (1960) Potential evapotranspiration estimates by the approximate energy balance method of Penman. J Geophys Res Atmos 65(10):3391–3413
Thom AS (1971) Momentum absorption by vegetation. Q J R Meteorol Soc 97(414):414–428
Whitaker S (1969) Advances in theory of fluid motion in porous media. Ind Eng Chem 61(12):14–28
Whitaker S (1973) The transport equations for multi-phase systems. Chem Eng Sci 28(1):139–147
Yang W, Quan Y, Jin X et al (2008) Influences of equilibrium atmosphere boundary layer and turbulence parameter on wind loads of low-rise buildings. J Wind Eng Ind Aerodyn 96(10):2080–2092
Acknowledgements
This work was partly supported by Natural Science Foundation of Xinjiang Province of China (No.2021D01A19).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Communicated by: H. Babaie.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, W., Wu, J. & Jiang, A. Numerical study on aerodynamic roughness of forest. Earth Sci Inform 15, 465–472 (2022). https://doi.org/10.1007/s12145-021-00735-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12145-021-00735-x