Abstract
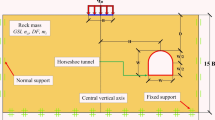
The present study investigates the ultimate bearing capacity (UBC) of a footing subjected to an eccentric load situated above an unlined horseshoe-shaped tunnel in the rock mass, following the Generalized Hoek-Brown (GHB) failure criterion. A reduction factor (Rf) is introduced to investigate the impact of the tunnel on the UBC of the footing. Rf is determined using upper and lower bound analyses with adaptive finite-element limit analysis. The study examines the influence of several independent variables, including normalized load eccentricity (e/B), normalized vertical and horizontal distances (δ/B and H/B) of the footing from the tunnel, tunnel size (W/B), and other rock mass parameters. It was found that all these parameters significantly affect the behavior of tunnel-footing interaction depending on the range of varying parameters. The findings of the study indicate that the critical depth (when Rf is nearly 1) of the tunnel decreases with increasing load eccentricity. The critical depth is found to be δ/B ≥ 2 for e/B ≤ 0.2 and δ/B ≥ 1.5 for e/B ≥ 0.3, regardless of H/B ratios. Additionally, the GHB parameters of the rock mass significantly influence the interaction between the tunnel and the footing. Moreover, this study identifies some typical potential failure modes depending on the tunnel position. The typical potential failure modes of the footing include punching failure, cylindrical shear wedge failure, and Prandtl-type failure. This study also incorporates soft computing techniques and formulates empirical equations to predict Rf using artificial neural networks (ANNs) and multiple linear regression (MLR).



























Similar content being viewed by others
Data availability
No datasets were generated or analysed during the current study.
Abbreviations
- UBC :
-
Ultimate bearing capacity
- GHB :
-
Generalized Hoek-Brown
- FEM :
-
Finite Element Method
- UB :
-
Upper Bound
- LB :
-
Lower Bound
- DLO :
-
Discontinuity Layout Optimization
- ANN :
-
Artificial Neural Network
- AFELA :
-
Adaptive Finite Element Limit Analyis
- MLR :
-
Multiple Linear Regression
- B :
-
Width of strip footing (m)
- H :
-
Horizontal distance of tunnel from central horizontal axis of footing (m)
- H/B :
-
Normalised horizontal position of tunnel relative to the footing width
- δ :
-
Vertical depth between the ground surface and crest of a tunnel (m)
- δ/B :
-
Normalised vertical depth of tunnel relative to the footing width
- e :
-
Load eccentricity (m)
- e/B :
-
Normalised load eccentricity with the footing width
- GSI :
-
Geological Strength index
- m i :
-
Material constant for intact rock
- D :
-
Disturbance factor of the rock mass
- σ ci :
-
Unconflined compressive strength (kPa)
- R f :
-
Reduction factor
- W :
-
Width of tunnel
- W/B :
-
Height to width ratio of tunnel
- q u :
-
Ultimate bearing capacity of strip footing resting on rock mass with underground tunnel (kPa)
- \(q_u^{\prime}\) :
-
Ultimate bearing capacity of strip footing resting on rock mass without underground tunnel (kPa)
- \(\sigma_1^{\prime}\) :
-
Maximum effective principal stress (kPa)
- \(\sigma_3^{\prime}\) :
-
Minimum effective principal stress (kPa)
- m b :
-
Material constant for rock mass strength
- a, s:
-
GHB constants
- γ :
-
Unit weight of rock mass (kN/m3)
- Q s :
-
Collapse multiplier load (kPa/m)
- RE :
-
Relative error
- MSE :
-
Mean square error
- RMSE :
-
Root means square error
- R 2 :
-
Coefficient of determination
- n :
-
Total number of samples
- \(y_i^{\prime}\) :
-
Predicted value
- y i :
-
Actual value or Testing data set
- \(\overline{y}\) :
-
Mean value
- \(\overline{y}_i\) :
-
Dependent variable
- Xi1 :
-
Independent variable
- β1 :
-
Slope coefficients
- \(\epsilon\) :
-
Residual error
- Nv :
-
Stability number
- σ s :
-
Ultimate bearing capacity of strip footing (kPa/m)
- σs/σci :
-
Stability factor
- W :
-
Height and width of the tunnel (m)
- W/B :
-
Normalised size of tunnel with the footing width
- NNs :
-
Number of neurons
- H n :
-
Hidden neurons
- x :
-
input variables
- J :
-
Number of input variables
- N :
-
Number of hidden neurons
- IW :
-
Weight matrices
- K :
-
Output neurons
References
Al-Tabbaa A, Russell L, O’Reilly M (1991) Model tests of footings above shallow cavities. Ground Eng 22(7):39–42
Atici U (2011) Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network. Expert Syst Appl 38(8):9609–9618. https://doi.org/10.1016/j.eswa.2011.01.156
Atkinson JH, Potts DM (1987) Stability of a shallow circular tunnel in cohesionless soil. Geotechnique 27(2):203–215
Baus RL, Wang MC (1983) Bearing capacity of strip footing above void. J Geotech Eng 109(1):1–14. https://doi.org/10.1061/(ASCE)0733-9410(1983)109:1(1)
Chauhan VB, Kumar P, Keawsawasvong S (2022) Limit analysis solution for ultimate bearing capacity of footing resting on the rock mass with a circular void subjected to line loading. Indian Geotech J 1–14. https://doi.org/10.1007/s40098-022-00676-2
Ciria H, Peraire J, Bonet J (2008) Mesh adaptive computation of upper and lower bounds in limit analysis. Int J Numer Meth Eng 75(8):899–944
Hoek E, Brown ET (1980) Empirical strength criterion for rock masses. J Geotech Eng Div 106(9):1013–1035
Hoek E, Carranza-Torres C, Corkum B (2002) Hoek-Brown failure criterion-2002 edition. Proc NARMS-Tac 1(1):267–273
Huckert A, Briançon L, Villard P, Garcin P (2016) Load transfer mechanisms in geotextile-reinforced embankments overlying voids: experimental and analytical approaches. Geotext Geomembr 44(3):442–456
Jaiswal S, Chauhan VB (2021) Ultimate bearing capacity of strip footing resting on rock mass using adaptive finite element method. J King Saud Univ-Eng Sci. https://doi.org/10.1016/j.jksues.2021.09.004
Jearsiripongkul T, Keawsawasvong S, Thongchom C, Ngamkhanong C (2022) Prediction of the Stability of various tunnel shapes based on hoek–brown failure Criterion using Artificial neural network (ANN). Sustainability 14(8):4533
Keawsawasvong S (2021) Bearing capacity of conical footings on Hoek-Brown rock masses using finite element limit analysis. Int J Comput Mater Sci Eng 10(3):2150015. https://doi.org/10.1142/S2047684121500159
Keawsawasvong S, Seehavong S, Ngamkhanong C (2022) Application of artificial neural networks for predicting the stability of rectangular tunnels in Hoek–Brown rock masses. Front Built Environ 8:17
Keawsawasvong S, Thongchom C, Likitlersuang S (2021) Bearing capacity of strip footing on Hoek-Brown rock mass subjected to eccentric and inclined loading. Transp Infrastruct Geotechnol 8:189–200. https://doi.org/10.1007/s40515-020-00133-8
Kiyosumi M, Kusakabe O, Ohuchi M (2007) Yielding pressure of spread footing above multiple voids. J Geotech Geoenviron Eng 133(12):1522–1531
Kiyosumi M, Kusakabe O, Ohuchi M (2011) Model tests and analyses of bearing capacity of strip footing on stiff ground with voids. J Geotech Geoenviron Eng 137(4):363–375. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000440
Krabbenhoft K, Lyamin A, Krabbenhoft J (2015) Optum computational engineering (OptumG2); Available at: https://www.optumce.com. Accessed 5 Nov 2023
Kumar P, Chauhan VB (2022a) Ultimate bearing capacity of a foundation on the rock media due to the presence of a circular void: design tables, failure mechanism, and recommendations. Arab J Geosci 15(15):1345. https://doi.org/10.1007/s12517-022-10620-6
Kumar P, Chauhan VB (2022b) On the eccentrically loaded strip footing resting over a circular cavity in the rock mass: adaptive finite-element analysis, observations, and recommendations. Int J Geomech 23(2):04022287. https://doi.org/10.1061/IJGNAI.GMENG-7985
Kumar P, Chauhan VB (2022c) Bearing capacity of strip footing resting above a circular void in the rock mass using adaptive finite element method. Innova Infrastruct Solut 7:72. https://doi.org/10.1007/s41062-021-00666-y
Kumar A, Chauhan VB (2023a) Advanced finite element limit analysis and machine learning for assessing the stability of square tunnels in rock slope. Transp Infrastruct Geotechnol 1–35. https://doi.org/10.1007/s40515-023-00338-7
Kumar P, Chauhan VB (2023b) Observations and recommendations for shallow foundation stability over dual cavities in rock mass under eccentric loading utilizing limit analysis. Arab J Sci Eng: 1–21. https://doi.org/10.1007/s13369-023-08524-y
Kumar P, Chauhan VB (2024a) Behavior of footing resting above Dual Circular Cavities in a Rock Mass: insights from an AFELA Study. Int J Geomech 24(1):04023248. https://doi.org/10.1061/IJGNAI.GMENG-9036
Kumar A, Chauhan VB (2024b) Stability Evaluation of Unlined Circular Tunnels in Sloping Rock Terrain using adaptive finite element Limit Analysis. Indian Geotech J 1–29. https://doi.org/10.1007/s40098-024-00903-y
Kumar A, Chauhan VB, Kumar P (2023) Integration of AFELA and machine learning for analysis of shallow foundation over horseshoe tunnel in rock mass. Model Earth Syst Environ: 1–20. https://doi.org/10.1007/s40808-023-018026
Lai VQ, Jitchaijaroen W, Keawsawasvong S, Chavda JT, Sae-Long W, Limkatanyu S (2023) Application of ANN and FELA for Predicting Bearing Capacity of Shell Foundations on Sand. Int J of Geosynth and Ground Eng 9(2):18. https://doi.org/10.1007/s40891-023-00437-y
Lai, VQ, Sangjinda, K, Keawsawasvong, S, Eskandarinejad, A, Chauhan, VB, Sae-Long, W, Limkatanyu, S (2022) A machine learning regression approach for predicting the bearing capacity of a strip footing on rock mass under inclined and eccentric load. Front Built Environ 8:962331. https://doi.org/10.3389/fbuil.2022.962331
Lee JK, Jeong S, Ko J (2014) Undrained stability of surface strip footings above voids. Comput. Geotech 62:128–135. https://doi.org/10.1016/j.compgeo.2014.07.009
Lee JK, Jeong S, Ko J (2015) Effect of load inclination on the undrained bearing capacity of surface spread footings above voids Comput. Geotech 66:245–252. https://doi.org/10.1016/j.compgeo.2015.02.003
Lee JK, Kim J (2019) Stability charts for sustainable infrastructure: Collapse loads of footings on sandy soil with voids. Sustainability 11(14):3966. https://doi.org/10.3390/su11143966
Marshall AM, Haji T (2015) An analytical study of tunnel–pile interaction. Tunn Undergr Space Technol 45:43–51. https://doi.org/10.1016/j.tust.2014.09.001
Meyerhof GG (1953) The bearing capacity of foundations under eccentric and inclined loads. In Vol. 1 of Proc., 3rd Int. Conf. on SMFE, 440–445. International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE), London
Millán MA, Galindo R, Alencar A (2021) Application of Artificial neural networks for Predicting the Bearing capacity of shallow foundations on Rock masses. Rock Mech Rock Eng 54:5071–5094. https://doi.org/10.1007/s00603-021-02549-1
Naghadehi MZ, Thewes M, Lavasan AA (2019) Face stability analysis of mechanized shield tunneling: an objective systems approach to the problem. Eng Geol 262:105307
Ngamkhanong C, Keawsawasvong S, Jearsiripongkul T, Cabangon LT, Payan M, Sangjinda K, Banyong R, Thongchom C (2022) Data-driven prediction of stability of rock tunnel heading: an application of machine learning models. Infrastructures 7(11):148
Nguyen DK, Nguyen TP, Ngamkhanong C, Keawsawasvong S, Lai VQ (2023) Bearing capacity of ring footings in anisotropic clays: FELA and ANN. Neural Comput Appl 35(15):10975-10996. https://doi.org/10.1007/s00521-023-08278-6
OptumCE (2020) OptumG2. Copenhagen, Denmark: Optum Computational Engineering. See https://optumce.com/. Accessed 05 Nov 2023
Sachpazis CI (1990) Correlating Schmidt hardness with compressive strength and Young’s modulus of carbonate rocks bull. Int Assoc Eng Geol 42(1):75–83. https://doi.org/10.1007/BF02592622
Saleh NM, Elsaied AE (2008) Performance of skirted strip footing subjected to eccentric inclined load Electron. J Geotech Eng 13:1–33
Salim NM, Lafta JS (2017) The impact of driving and loading piles on existing tunnel. Imp J Interdiscip Res 3(7):2454–1362
Shen Z, Feng X, Gourvenc S (2016) Undrained capacity of surface foundations with zero-tension interface under planar V-H-M loading Comput. Geotech 73:47–57. https://doi.org/10.1016/j.compgeo.2015.11.024
Sirimontree S, Keawsawasvong S, Ngamkhanong C, Seehavong S, Sangjinda K, Jearsiripongkul T, Thongchom C, Nuaklong P (2022) Neural network-based prediction model for the stability of unlined elliptical tunnels in cohesive-frictional soils. Buildings 12(4):444
Sloan SW (2013) Geotechnical stability analysis. Geotechnique 63(7):531–572
Soleiman DM, Lazemi HA, SaeedModaghegh HR (2019) Estimation of the drop modulus using the brittleness index of intact rock and geological strength index of rock mass, case studies: Nosoud and Zagros tunnels in Iran. Model Earth Syst Environ 5:479–492. https://doi.org/10.1007/s40808-019-00577-z
Wang MC, Badie A (1985) Effect of underground void on foundation stability. J Geotech Geoenviron Eng 111(8):1008–1019
Wu G, Zhao M, Zhang R, Liang G (2020) Ultimate bearing capac-ity of eccentrically loaded strip footings above voids in rock masses. Comput Geotech 128:103819. https://doi.org/10.1016/j.compgeo.2020.103819
Xiao Y, Zhang M, Zhou Z, Hou Z, Lv J, Tang M, Zhang R (2023a) Ultimate bearing capacity of strip footings above rectangular voids in Hoek-Brown rock masses. Comput Geotech 161:105589
Xiao Y, Zhao M, Zhang R (2023b) Seismic bearing capacity for strip footings above voids in cohesive-frictional soils. Earthq Spectra 39(1):269–287
Xiao Y, Zhao M, Zhao H, Zhang R (2018a) Finite element limit analysis of the bearing capacity of strip footing on a rock mass with voids. Int J Geomech 18(9):04018108. https://doi.org/10.1061/(ASCE)GM.1943-5622.0001262
Xiao Y, Zhao M, Zhao H (2018b) Undrained stability of strip footing above voids in two-layered clays by finite element limit analysis. Comput Geotech 97:124–133
Yang XL, Yin JH (2005) Upper bound solution for ultimate bearing capacity with modifed hoek-brown failure criterion. Int J Rock Mech Min Sci 42:550–560. https://doi.org/10.1016/j.ijrmms.2005.03.002
Yodsomjai W, Keawsawasvong S, Lai VQ (2021) Limit analysis solutions for bearing capacity of ring foundations on rocks using Hoek-Brown failure criterion. Int J Geosynth Ground Eng 7:29. https://doi.org/10.1007/s40891-021-00281-y
Zhang R, Feng M, Xiao Y, Liang G (2022) Seismic bearing capacity for Strip footings on Undrained Clay with Voids. J Earthquake Eng 26(9):4910–4923
Zhang X, Wang M, Li J, Wang Z, Tong J, Liu D (2020) Safety factor analysis of a tunnel face with an unsupported span in cohesive-frictional soils. Comput Geotech 117:103221
Zhou H, Zheng G, He X, Xu X, Zhang T, Yang X (2018) Bearing capacity of strip footings on c–φ soils with square voids. Acta Geotech 13(3):747–755
Funding
None.
Author information
Authors and Affiliations
Contributions
Aayush Kumar: Data curation, Numerical Modelling, Validation, Software, Methodology, Writing original draft, Vinay Bhushan Chauhan: Conceptualisation, Data curation, Writing - review & editing, Project administration, Supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Communicated by: Hassan Babaie
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kumar, A., Chauhan, V.B. Evaluating the impact of eccentric loading on strip footing above horseshoe tunnels in rock mass using adaptive finite element limit analysis and machine learning. Earth Sci Inform 17, 4441–4471 (2024). https://doi.org/10.1007/s12145-024-01380-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12145-024-01380-w