Introduction

Permeability is a fundamental input for numerical reservoir simulation. Predicting the permeability along and between wells to obtain the 3D spatial distribution is a challenging task in reservoir modeling. A poor prediction will lead to unreliable dynamic models that cannot describe the actual past, current, and future flow performance of oil and gas reservoirs (Cannon 2018; Alizadeh et al. 2022).

Permeability can be measured using core sampling and well-test analysis. However, these methods are costly, time-consuming, and accord too limited subsurface coverage. Conventionally, permeability is estimated from porosity via linear regression analysis. However, this model ignores the lack of a basic relationship between porosity and permeability, as intervals with the same porosity but different permeability may exist in the reservoir. Moreover, some carbonate reservoirs exhibit low porosity and high permeability due to fracturing (Tiab and Donaldson 2015). Some empirical models exist in the literature for estimating permeability relying on porosity and irreducible water saturation (Timur 1968; Coates and Denoo 1981) or resistivity and fluid density (Tixier 1949; Coates and Dumanoir 1973). Nevertheless, these models require the definition of certain coefficients that necessitate laboratory measurements, which is rarely the case, or general principles and prior knowledge. Due to the lack of generalized and accurate predictive paradigms, it is an incentive for researchers to build new rigorous predictive models with wider applicability and higher accuracy.

Several researchers involve logs other than porosity to predict permeability via multiple linear regression analysis (Amaefule et al. 1993; Al-Ajmi et al. 2000; Desouky 2005, and Khalid et al. 2020). However, this approach cannot be applied in reservoirs where complex non-linear relationships exist between well logs and permeability.

To tackle such challenges, Machine Learning (ML) has been used as a regression tool for improving permeability prediction. Several researchers compared the conventional estimation methods and ML models in estimating permeability. Akande et al. (2017) applied a hybrid particle swarm optimization (PSO) algorithm and support vector regression model (SVR) for improving the performance of permeability prediction. Gu et al. (2021) utilized PSO to enhance the performance of Extreme Gradient Boosting (XGBoost) model in permeability prediction. However, the previous two studies didn’t clarify a systematic approach to select the optimum parameters of PSO that can determine the best hyperparameters of SVR and XGBoost models. Kamali et al. (2022) used four ML algorithms for predicting permeability, including the group method of data handling, polynomial regression, SVR, and decision trees, and observed that the group method outperformed other models. Nevertheless, this approach predicts permeability from core data, not from well logging ones. This is a significant shortcoming to building a reliable 3D model that requires estimating permeability along the reservoir profile in each well. Anifowose et al. (2019) integrated well logging data and seismic attributes using different ML methods for improved permeability prediction. However, core data weren’t used in the study to validate the accuracy of the developed predictive models. Al-Mudhafar (2019) compared Bayesian model averaging and LASSO regression methods with the conventional linear regression model for predicting permeability from well logs. Results show that the performance of the three models is roughly similar and didn’t capture the true relationship between the logs and permeability accurately. Djebbas et al. (2023) used an adaptive neuro-fuzzy inference system to integrate the flow units (FUs) of the reservoir and well logs to predict core permeability. However, the reservoir FUs were randomly distributed, and the study didn’t provide a systematic approach to predict the FUs and permeability from the logs along the reservoir profile of the wells. The previously mentioned ML studies have significant shortcomings in the application of the developed models for developing continuous permeability logs along the profile of wells to be further populated in 3D. The present study provides a systematic approach based on artificial neural networks (ANNs) to predict the 3D spatial distribution of permeability in the Lower Safa sand reservoir, JG field, Abu El-Gharadig basin, Egypt, using core and well logging data. This study aims to 1) determine the reservoir quality and heterogeneity using core data and 2) develop an ANN-based permeability prediction approach to predict permeability logs along the reservoir profile of wells to be further populated in 3D.

Location and geology of the study area

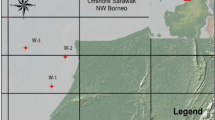
The proposed approach was applied to the Lower Safa member of the Khatatba Formation in the JG field. JG is one of the main oil fields that was discovered in the west of the North East of Abu El-Gharadig basin (NEAG concession) in 2001. It is located between longitudes 28° 06′ to 28° 17′ E and between latitudes 30° to 30° 34′ N. It lies some 35 km NE of the Bed-3 gas field, 25 km NE of the BED-17 oil field, and NW of the JD Field, as shown in Fig. 1.

Fig. 1
figure 1

Location map of JG field (Mahmoud et al. 2019)

Full size image

Khatatba Formation was deposited in the Jurassic age above Ras Qattara Formation, as indicated in Fig. 2. It consists of four lithological members: Lower Safa, Kabrit, Upper Safa, and Zahra members. It is characterized by remarkable variation in facies coinciding with a remarkable thickness variation. The sandstone of the Lower Safa member constitutes the main reservoir unit in the field (Moustafa et al. 2008). The member is widely extended along the field as amalgamated channels created by an active braided channel system with thick and massive sandstone bodies with very little flood plain represented by small shale strikes (Fig. 3).

Fig. 2
figure 2

Generalized stratigraphic column of the Western Desert (Shalaby et al. 2012)

Full size image
Fig. 3
figure 3

Photomicrograph image for a core slab of the Lower Safa sand reservoir (the dark color indicates the minor floodplain shale deposits)

Full size image

The JG field structure is an elongated E-W fault dip closure bounded by the Cretaceous Abu El-Gharadig basin bounding fault to the south. A series of smaller ENE-WSW and NW-SE trending faults bisect the structure (Mahmoud et al. 2019).

Materials and methods

Two wells were selected from the JG field relying on the data availability and coverage. The wells targeted the Lower Safa sand reservoir of the Khatatba Formation. Conventional well logs, involving gamma-ray (GR), neutron (NPHI), density (RHOB), and deep resistivity (RES_DEEP) data every 0.1524 m, are available from the two wells. The details of different methods and algorithms applied during reservoir evaluation are discussed in the following subsections:

Routine core analysis

Routine core analysis (RCA) was carried out on a total of 225 core plug samples from the two wells. RCA includes porosity (Φ) measured by a helium porosimeter and horizontal permeability (K) determined by a nitrogen permeameter. This aids in determining the quality and heterogeneity of the reservoir.

Core-log integration

Depth shifting of core to match log depths is the initial step in calibrating core data with wireline logs. The cores are often mishandled, resulting in notoriously inaccurate marked depths on core samples. To tackle this problem, the core gamma-ray log is compared with the wireline gamma-ray log (Lucia 2007). Thereafter, the approach of artificial neural network was used to integrate core permeability with the influential well logs to predict permeability logs and obtain a reliable 3D permeability model.

Permeability prediction using artificial neural networks

Artificial neural networks (ANNs) are deep learning algorithm that try to imitate the processing steps of the human brain to investigate the relationships between the inputs and the outputs. They are composed of parallel layers involving several neurons: the input layer that represents the input features, the hidden layer that is optimized by the trial-and-error process, and the output layer that constitutes the target or the desired variable. To transfer the data throughout the layers, certain activation functions are used, and a certain training algorithm is selected. The data is partitioned into different sets to evaluate the performance of the model: the training set for training the model and the validation and testing sets to check the model’s validity and reliability (Hinton et al. 2006; Del Castillo et al. 2012).

The ANN model has different hyperparameters that must be tuned to improve the prediction performance, involving the number of hidden layers, the number of hidden neurons per layer, and the type of activation function.

There are several techniques of cross-validation to assess the model performance, such as k-fold cross-validation and random subsampling. K-fold cross-validation involves partitioning the training data into k-folds (each partition is called a fold), where “k-1” folds are used for training the model and one is held back for validating the model accuracy. This step is repeated k times iteratively, where each fold of the dataset can be used for validation. The overall model performance is computed by averaging the performance results across all iterations (Brownlee 2016). In this study, random subsampling was used, where the dataset was randomly subdivided into three sets: the training set to train the ANN model and the validation and testing sets to check the model accuracy. Three statistical metrics were used to evaluate the model performance, namely the coefficient of determination (R2), mean absolute error (MAE), and mean squared error (MSE).

The developed ANN model was used to predict the permeability logs. Ultimately, the predicted logs were populated via the Sequential Gaussian Simulation algorithm to obtain the 3D permeability distribution of the reservoir.

Sequential Gaussian Simulation

Deutsch and Journel (1992) and Olea (2000) defined the Sequential Gaussian Simulation (SGS) as a stochastic geostatistical algorithm performed in the spatial domain to generate realizations using multivariate normal random functions.

The SGS can be summarized in the following steps:

  1. 1-

    Transform the original data into a standard normal distribution (mean of 0 and standard deviation of 1).

  2. 2-

    Define a random path through the grid cells such that each unconditioned cell is visited once. Thereafter, search for all neighboring data and previously simulated cells.

  3. 3-

    Construct the conditional distribution by simple kriging (SK). This determines the mean of the Gaussian distribution and the variance. The local cumulative distribution function (CDF) can then be defined. SK uses an affine linear equation for spatial prediction, where:

    $$\widehat{Z}\left(x\right)=m+{\sum }_{i=1}^{n}{\lambda }_{i}\left[Z \left({x}_{i}\right)-m\right]$$
    (1)

    Where Ẑ(x) is the kriging estimate at unsampled locations, m is the mean of the random variable Z(xi), and n is the number of data samples used in kriging.

    By minimizing the squared errors, ε2= [Z(x) − Ẑ(x)] 2, the kriging system is obtained. It can be expressed by:

    $$\sum_{i=1}^{n}{\lambda }_{i}{C}_{ij}={C}_{0j}$$
    (2)

    Where Cij is the covariance matrix between the data values at sampled locations “i and j”, C0j is the covariance matrix between the unsampled data at the estimation location and the sampled data, and \({\uplambda }_{\text{i}}\) is the matrix of the kriging weights.

    By determining the covariance between different data, we can solve for the kriging weights. The simple kriging estimation variance, σ2(x0), can then be computed as:

    $${\sigma }^{2}\left({x}_{0}\right)=variance-\sum_{i=1}^{n}{\lambda }_{i}{C}_{0j}$$
    (3)
  4. 4-

    Draw a simulated value from the conditional distribution (Monte Carlo Simulation).

  5. 5-

    Assign the simulated value to the grid as data.

  6. 6-

    Repeat steps 3 to 6 until all cells have been simulated. This creates a single realization.

  7. 7-

    Back-transform all the data and simulated values into the original space.

  8. 8-

    Check the accuracy of the model by comparing the distributions of the input data and the distributed property (Jensen 2000; Pyrcz and Deutsch 2014, and Ma and Zhang 2019).

Fig. 4 shows the workflow for the proposed ANN approach for predicting and populating permeability logs in 3D.

Fig. 4
figure 4

Flow chart of the proposed methodology to predict and populate permeability logs in 3D

Full size image

Results and interpretation

In this section, a detailed comparison between the conventional and the proposed ANN approaches for predicting core permeability is provided. The mathematical equation of the developed ANN model is discussed. Application of this model to develop and distribute permeability logs of the two studied wells in 3D is also presented.

Permeability modeling using the conventional approach

The statistical parameters of the core porosity (Φ), permeability (k), and logarithm of k (log k) of the two studied wells determined using the routine core analysis are presented in Table 1. Fig. 5 illustrates the fitting relationship between Φ and log k, where log k = 24.296 Φ – 2.132. The figure depicts a poor correlation (R2 = 0.66) and a high degree of scatter between the two properties, where permeability varies by several orders of magnitude for the same porosity. This introduces significant uncertainties in the modeled permeability (Fig. 6), which led us to the application of deep learning to achieve better results. Table 2 illustrates the evaluation metrics for the modeled permeability using the conventional fitting relationship.

Table 1 The statistical parameters of core porosity, permeability, and logarithm of permeability of the two studied wells
Full size table
Fig. 5
figure 5

A cross plot of core porosity vs. logarithm of core permeability of the two studied wells

Full size image
Fig. 6
figure 6

A cross plot of the predicted log k and log core k

Full size image
Table 2 The evaluation metrics for the developed permeability model
Full size table

Core-log integration

Core-log depth match was performed, where the core GR is calibrated to the GR log, as indicated in Fig. 7. Fig. 7a shows a difference in depths between the two curves (about 9 meters), and Fig. 7b clarifies that the two curves overlap after applying the shift.

Fig. 7
figure 7

Core GR and GR log curves of the first studied well: (a) before applying the depth shift and (b) after applying the depth shift

Full size image

Three well logs were selected to build the reservoir permeability model, including the effective porosity (PHIE), bulk density (RHOB), and deep resistivity (RES_DEEP) logs. The target variable of the model is the log k. Fig. 8 shows the selected logs of one of the studied wells, and Table 3 clarifies their statistical parameters. Permeability has a direct relation to PHIE, where intervals of high PHIE exhibit high permeability. RHOB log is a function of the total formation porosity. There is an inverse relation between bulk density and permeability, where low-bulk density zones exhibit high porosity and permeability. The resistivity log infers the formation’s fluid saturation and hydrocarbon content that is directly related to the permeability of the reservoir. The PHIE log was developed by combining the two porosity logs (neutron and density) in clean sand intervals. In shaly sand intervals (with high GR), the shale volume is eliminated from the calculations. The GR log indicates the shaly and non-shaly (clean) reservoir intervals and is used in computing the shale volume. This is critical for obtaining accurate effective porosity estimates, which in turn have a pivotal effect on permeability. RHOB and RES_DEEP are raw logs. The cross plots and histograms of the well logs and the target variable are shown in a matrix plot diagram (Fig. 9).

Fig. 8
figure 8

The selected well logs to build the permeability model of the Lower Safa sand reservoir

Full size image
Table 3 The statistical parameters of the selected well logs
Full size table
Fig. 9
figure 9

Matrix plot diagram of the three selected logs (input) and log K (target)

Full size image

Permeability modeling using the ANN approach

The second approach used in this study to predict permeability from the influential well logs is the artificial neural network. The core and logging data were used to construct a feed-forward backpropagation model using 65% of the data for training (147 samples), 17.5% for validation (39 samples), and 17.5% for testing and checking the models’ reliability and accuracy (39 samples). The inputs are normalized between 0 and 1 through the following formula:

$${X}_{n}=\left(X-{X}_{minimum}\right) / \left({X}_{maximum}-{X}_{minimum}\right)$$
(4)

Where Xminimum is the minimum value of input data and Xmaximum is its maximum value.

The algorithm of backpropagation is employed for adjusting the weights and biases of the network to minimize the error for both the training and validation datasets. It must be highlighted that the mathematical model was created via the Matlab programming language.

Architecture and mathematical description of the ANN model

The developed ANN model consists of 3 layers: the input layer with the three previously mentioned predictors (logs), the hidden layer with 16 neurons, and the output layer with only one neuron for the logarithm of core permeability. The Tan-Sigmoid (Tan sig) and linear activation functions are used for the input and hidden layers, respectively. For training the network, the Levenberg-Marquardt (lm) optimization algorithm is applied. Lm was designed to approach second-order training speed without having to compute the Hessian matrix (Beale et al. 2010). If the performance metric has the form of a sum of squares, i.e., MSE (as is typical in training feedforward networks), then the Hessian matrix (H) can be approximated as:

$$H={J}^{T}*J$$
(5)

and the gradient (g) can be calculated as:

$$\text{g}={J}^{T}*e$$
(6)

Where e is the vector of the network errors and J is the Jacobian matrix that contains first derivatives of the network errors with respect to the weights and biases.

The lm algorithm uses this approximation in the following Newton-like update:

$${x}_{k+1}={x}_{k}-{\left[{J}^{T}.J+\mu I\right]}^{-1}{J}^{T}e$$
(7)

Further details regarding the lm algorithm are found in Beale et al. (2010).

To prevent overfitting, the Error-Stopping criterion was carried out. The number of epochs was selected empirically as 15. The developed model’s parameters are presented in Table 4. The ANN model architecture is shown in Fig. 10. Table 5 illustrates the weights and biases between the input, hidden, and output layers.

Table 4 The parameters of the developed ANN model
Full size table
Fig. 10
figure 10

The developed ANN model architecture

Full size image
Table 5 Weights and biases between the input, hidden, and output layers
Full size table

The mathematical ANN equation can be extracted from the developed model with the weights and biases that are required to calculate the logarithm of permeability, as follows:

$$Log K=\left[{\sum }_{j=1}^{n}{w}_{j}.Tan si\text{g}\left({\sum }_{j=1}^{n}{w}_{i}.{X}_{ni}+{b}_{1}\right)\right]+{b}_{2}$$
(8)

Where i is the number of inputs, “j” is the number of hidden neurons, \({w}_{i}\) is the input layer weight, \({w}_{j}\) is the hidden layer weight, b1 is the input layer bias, b2 is the output layer bias, and Xni is the normalized input data.

Performance of the ANN model

In this section, the performance of the permeability prediction of the ANN model for the training, validation, and testing datasets is evaluated. The Error-Stopping criterion is indicated in Fig. 11. The figure clarifies that the training process had been stopped when the performance of the validation set was not improved anymore. The loss function of the training and validation datasets (MSE) decreases to a point of stability with a minimal gap between the two values. This reveals that the model will have good generalization performance. The best performance occurs at epoch 5, where MSE is 0.19 for the training set, 0.25 for the validation set, and 0.24 for the testing set.

Fig. 11
figure 11

The Error-Stopping criterion of the developed ANN model

Full size image

Fig. 12 shows a plot of the predicted logarithm of permeability and logarithm of core permeability of the training, validation, and testing sets of the developed ANN model. The evaluation metrics of the developed model for the three sets are presented in Table 6. It is evident that strong correlation and small error exist for the three sets, where R2 = 0.90, 0.91, and 0.88 for the training, validation, and testing sets, respectively. MAE = 0.32, 0.37, and 0.37, while MSE = 0.19, 0.25, and 0.24 for the three sets, respectively. The data samples are much closer to the 45-degree line than in the conventional model. This is attributed to the ability of the model to capture the complex non-linear relationships between input features and the target, hence providing better accuracy. Fig. 13 indicates a plot of the predicted permeability values vs. the core permeability of the whole reservoir samples.

Fig. 12
figure 12

Cross plots of the predicted logarithm of permeability and logarithm of core permeability of (a) the training dataset, (b) validation dataset, and (c) testing dataset

Full size image
Table 6 The evaluation metrics of the ANN model for the training, validation, and testing datasets
Full size table
Fig. 13
figure 13

A cross plot of the predicted permeability vs. core permeability of the whole reservoir samples

Full size image

Investigation of feature importance

In this study, the impact of features on permeability prediction results was investigated using the SHAP tool (SHapley Additive exPlanations). SHAP uses situational importance to measure the feature importance, i.e., the contribution of each feature to a prediction output at each specified query point (Lundberg 2017). The method selects samples that provide estimates for feature importance by calculating how much variation the predictor promotes for a locally given point. The predictor’s contribution (Φj (x)) is compared to its expected contribution (E[xj]), as expressed below, with βj depending on a subset of input features for a nonlinear case.

$${\Phi }_{j}\left(x\right)={\beta }_{j}.\left({x}_{j}-E\left[{x}_{j}\right]\right)$$
(9)

Fig. 14 clarifies a bar plot for the absolute SHAP values of the three selected features of the ANN model. The figure illustrates that the effective porosity log is the most significant feature that has the highest impact on the predicted output, followed by the deep resistivity log, whereas the bulk density log has the lowest impact.

Fig. 14
figure 14

A bar plot for the absolute SHAP values of the three features (well logs)

Full size image

Predicting and populating the permeability logs

The developed ANN model was used to predict the permeability logs (k-logs) in the logged reservoir intervals of the two studied wells (Fig. 15). The k-logs were upscaled and populated in the geological model by setting the appropriate variogram and applying the Sequential Gaussian Simulation method (SGS). The parameters of the developed model are presented in Table 7. Fig. 16 indicates the histograms of the input data, upscaled cells, and the distributed permeability. The figure clarifies that the distributed permeability honors the input and upscaled cells’ distribution accurately. The 3D permeability distribution for the reservoir is indicated in Fig. 17.

Fig. 15
figure 15

The permeability logs of the logged reservoir intervals of (a) the first well and (b) the second well

Full size image
Table 7 The parameters of the permeability model
Full size table
Fig. 16
figure 16

Histograms of the k-logs, upscaled cells, and the distributed property (permeability)

Full size image
Fig. 17
figure 17

The 3D permeability distribution of the Lower Safa sand reservoir

Full size image

Discussion regarding the developed ANN model

Based on the obtained results by the ANN approach, it is evident that the ANN model exhibits better prediction performance than the conventional model, where R2 between the predicted permeability and core permeability is ≥ 0.88 for the training, validation, and testing datasets. MAE and MSE for the three sets are reasonably lower than that of the conventional model. The conventional model fails to capture the complex non-linear relationship between porosity and the logarithm of permeability since it assumes linearity. This results in a poor predictive model with R2 = 0.66, MAE = 0.66, and MSE = 0.7. Building the ANN model using well logs (RHOB and RES_DEEP) other than porosity provides better prediction performance compared to traditional porosity-to-permeability estimation since other factors affect the permeability variation than porosity. The developed model was able to capture the intricate relationships between the predictors and target variable, resulting in a model with a much lower bias than the conventional model. Equally important is to highlight that the ANN model underestimates some high permeability values and overestimates others since the model ignores some values while fitting the pattern in the data. Such performance occurs at the expense of the ability of the model to fit the unseen data (Negnevitsky 2005). The studied reservoir has a very wide range of permeability, spanning from 0.01 to 2762 md. If the model fits the whole data range, overfitting will occur. To avoid this problem, the data was subsampled, and the pertinent hyperparameters were properly tuned for their optimized values. This aids in apprehending the permeability heterogeneity and developing the best-performing predictive model by detecting the error of the testing dataset that hadn’t been used to train the model. Hitherto, systematic work concerning the role of diagenesis (type and extent) in controlling rock permeability has not been addressed, which can be introduced in the future.

Conclusions

Accurate permeability prediction is challenging in reservoir modeling. This study provides a systematic approach based on artificial neural networks for predicting and populating permeability logs of the Jurassic Lower Safa sand reservoir of the Khatatba Formation. The conventional model fails to model the permeability accurately, resulting in a model with a high bias. A rigorous ANN predictive model was developed to integrate the core permeability with the influential well logs, and its performance was evaluated. Statistical analysis reveals that the model has an outstanding performance in comparison with the conventional regression model, where R2 between the predicted and core permeability = 0.9. The developed model was used to predict the K-logs that were finally populated in the geological model via the Sequential Gaussian Simulation geostatistical method to obtain the 3D permeability distribution. The outcomes of the study will aid users of deep learning to make informed choices on the appropriate ANN models to use in clastic reservoir characterization for more accurate permeability predictions with limited available data.