Abstract
This paper addresses uncertainty quantification in manually created 3D geological models of complex regions with sparse data, crucial for e.g. safety and exploration planning. Current models lack such assessments, which is particularly problematic for non-expert stakeholders. The Czech Geological Survey (CGS) developed a workflow to evaluate and visualize uncertainty in such models. Unlike models of geologically simpler areas with rich input data, these models based on sparse input data are created manually and rely on specific model-based interpretations that assume certain tectonic regime or deformation style known from a broader region and from field studies of rock outcrops. The classic uncertainty calculation based on the comparison of a range of (semi-) automatically created models cannot be employed for manually-created stand-alone geological models, and no suitable methodology has yet been determined for such cases. The methodology presented by the CGS considers three sources of uncertainty: the local lithological complexity, the distance to faults, and the so-called general uncertainty - a coefficient that increases with depth. The resulting uncertainty, normalized to the interval < 0;1>, is then reduced in the vicinity of available input data sources (boreholes, geological/geophysical profiles, etc.). The result comprises a 3D grid of the relative uncertainty of the given geological model, which can then be imported into the 3D software tools available to the users of the respective geological model. Demonstrated on the Čertovka site, a potential deep geological repository of high-level radioactive waste, the resulting uncertainty 3D grid guides users in understanding model limitations and can guide subsequent geological explorations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
3D geological models can never be totally accurate since they depict rock volumes that are not directly observable. The quantified uncertainty of geological models is the key attribute when used in subsequent geoscientific and engineering workflow stages, i.e. numerical simulations (e.g. groundwater hydraulic models concerning environmental issues or geomechanical models of the stability of underground excavations), exploration (e.g. the optimization of the subsequent drilling/geophysical fieldwork phases), design (e.g. the optimum location, extent and orientation of the underground spaces or large buildings founded more meters below surface) and construction work (e.g. the selection of the most suitable excavation technologies for particular rock environments). In all the above cases, a knowledge of the uncertainty of the input geological model is crucial in the decision-making process in terms of the economic, safety and environmental impacts of the respective construction. For example, uncertainty related to the location of the boundaries between distinct geological bodies is often one of the main sources of uncertainty with respect to mineral, oil and gas mining projects, and this factor must be assessed in terms of its potentially significant impact on the ore tonnage/hydrocarbon reserves and, thus, on the profitability of the project.
As a consequence of the increasing use of geological models over the last few decades, considerable research has been devoted in recent years to the estimation of the uncertainty inherent in geological models (Lecour et al. 2001; Tacher et al. 2006; Jessell et al. 2010; Lindsay et al. 2012, 2014; Wellmann and Regenauer-Lieb 2012; Wellmann et al. 2014, 2018; Yamamoto et al. 2014; Bond 2015; Schneeberger et al. 2017; de la Varga et al. 2019; Pirot et al. 2022; Huang et al. 2023). Although such papers often provide detailed descriptions, and attempt to explain and classify the various sources of uncertainty in geological models, they suggest solutions to calculate uncertainties only for those models that are created using (semi-) automatic approaches, e.g. via inversion, geostatistics, etc. They fail to present applicable workflows for cases in which geological models are created manually and in a single version, despite the broad consensus that a knowledge of the uncertainty of geological models is essential in terms of their practical use.
This study presents a new and general methodology for estimating the uncertainty of such manually created models of geologically complex areas that are covered by a low density of geoscientific input data, and briefly demonstrates its application.
This issue is typically, but not exclusively, related to the geological modelling of relatively extensive areas covered by large archive datasets of highly variable density, original purpose of creation and quality. The approach described below stems from explicit geological modelling by the Czech Geological Survey of the Variscan crystalline of the Bohemian Massif and its sedimentary cover, which is significantly obscured by quarternary deposits, soil and vegetation.
The majority of the resulting geological models were based on sparse and heterogeneous data often due to the limited number of deep cored boreholes and geophysical surveys in the modelled regions. Moreover, the geology in the Czech Republic comprises primarily crystalline complexes that exhibit several phases of metamorphism, ductile deformation and faulting, as well as magmatic intrusions, all of which result in a high degree of complexity. All these factors contribute to the geometrical discontinuity of the rock bodies and other geological structures and, thus, the mathematically hardly predictable geometries of the related geological models compared to e.g. models of exclusively sedimentary environments. Hence, it is practically impossible to use automated methods for the creation of a set of reasonable models that are generated (semi-) automatically applying the implicit approach, using interpolation algorithms and geostatistical approaches (implicit modelling methodologies are described e.g. in Jørgensen et al. 2015; Wellmann and Caumon 2018; Amarante et al. 2019; Jin et al. 2020; van der Grijp et al. 2021; Guo et al. 2022a, 2022b; Liu et al. 2022; Schorpp et al. 2022; Veliz et al. 2023) or Monte Carlo techniques (González-Garcia and Jessell 2016; Wellmann and Caumon 2018; Pakyuz-Charrier et al. 2018a, 2018b, 2019; Yang et al. 2019; de la Varga et al. 2019; Yin et al. 2020; Ouyang et al. 2023; Huang et al. 2023). Consequently, 3D geological models of the Czech crystalline must be usually created manually based both on the available input data and the extensive but subjective field experience of the geologists involved, and thus relying on a specific model interpretation that assumes e.g. a certain tectonic regime or style of deformation as observed on rock outcrops in the modelled area and its wider surroundings. In such cases, the classic principle of performing uncertainty calculations via the comparison of a range of models cannot be adopted since insufficient geoscientific input data is available for the application of the implicit approach to produce series of reasonable geological models. Additionally, it is not possible to determine a mathematically reliable approach to treating uncertainty as an error propagated from the input data through the modelling process due to the non-availability of the rigorously collected initial uncertainty values of the acquisition process of the geoscientific input data. These data are often inaccurate, but their credibility cannot be exactly determined.
In such situations, it is not possible to apply the classic uncertainty calculation method based on series of model realizations of one region of interest (e.g. Lindsay et al. 2012; Wellmann et al. 2014 or Amarante et al. 2019) since it necessarily requires a range of different models of the same rock volume. To the best of our knowledge, no methodology has been published to date for the quantification of the uncertainty of a single model. Therefore, the only practically applicable approach is that described in this paper. The approach is robust, practically focused and universal, and emerged over the last ten years as a result of the construction of a large number of 3D geological models at various scales and for a wide range of purposes.
The uncertainty of such geological models is thus, currently, not spatially quantified, rather it is usually presented to model users and stakeholders in vague terms in accompanying reports. However, it is important that the uncertainty inherent in geological models be expressed quantitatively and relatively precisely for the purposes of, for example, safety analyses or geological exploration planning. Hence, the Czech Geological Survey has developed a methodology for evaluating and visualising uncertainty in manually created explicit models. This methodology assesses 3 sources of uncertainty:
-
(1)
The local lithological complexity.
-
(2)
The distance to faults.
-
(3)
So-called general uncertainty - a coefficient that increases with depth.
The resulting uncertainty is then decreased with increasing proximity to the available input data sources, e.g. boreholes, geological/geophysical profiles, etc. This approach primarily covers all sources of larger-scale spatial geoscientific data that are used as input for the explicit manual construction of geological models in order that it can cover the uncertainties that originate from them.
The workflow results in a 3D grid of uncertainty values for the whole of the modelled rock environment volume. Admittedly, the values obtained are only semi-quantitative (based partly on expert estimates) and relative; however, our 10 years of experience with such modelling indicates that it is not possible to develop significantly more accurate general procedure for such kind of geological models. The main constraint to the use of more accurate approaches lies principally in the highly heterogeneous quality of the geoscientific input data, which cannot be processed applying an accurate quantitative approach. For these reasons and also as it is impossible to create a series of model realizations of a single region, our current methodology does not allow for integration of probability methods, such as uncertainty qualification based on the Bayesian approach.
Such a modelling approach differs substantially from the above-mentioned implicit creation of usually smaller-scale 3D models in simpler geological settings, e.g. for the more detailed exploration stages of mineral deposits or oil/gas reservoirs. In such cases, large data sets obtained via intensive and single-purpose exploration campaigns are usually available that allow for the construction of implicit geological models. The uncertainty of such models is then quantified by defining the range of model input parameters and the automated construction of various models of the site using variations of the input parameters e.g. applying the Monte-Carlo method. The resulting spectrum of geological models of the examined rock volume is then used to quantify the variability within the modelled volume, which is then recalculated to the form of uncertainty values (Wellmann and Caumon 2018; Pakyuz-Charrier et al. 2018a, 2018b, 2019; Lyu et al. 2021). The repeated running of a model construction algorithm occurs with parameters that vary within the given ranges, e.g. using random variation, e.g. the Monte Carlo method (González-Garcia and Jessell 2016; Wellmann and Caumon 2018; Pakyuz-Charrier et al. 2018a, 2018b, 2019; Cremon et al. 2018; Yang et al. 2019; de la Varga et al. 2019; Yin et al. 2020; Sadeghi and Cohen 2023; Ouyang et al. 2023; Huang et al. 2023) or using geostatistical methods (Mery et al. 2017; Wellmann and Caumon 2018; Amarante et al. 2019; Jin et al. 2020; van der Grijp et al. 2021Guo et al. 2022a, 2022b; Veliz et al. 2023; Sadeghi and Cohen 2023) or machine learning methods, probabilistic geomodelling methods, etc. (Wellmann and Caumon 2018; Kuhn et al. 2019; de la Varga et al. 2019; Krajnovich et al. 2020; van der Grijp et al. 2021; Shahri et al. 2023).
Although our methodology applies well-known and relatively simple techniques (for example, the concept of information entropy to determine the uncertainty of the complexity of the local lithology) and the subjective quantification of the credibility of the spatial geoscientific input data, it is innovative in several other respects. Firstly, unlike other approaches to determining the uncertainty of geological models, it can be used for single models, that are often produced in the low input data density modelling of geologically complex areas. The second advantage concerns the versatility of its application, which includes the potential introducing different input data for its application to a particular model if needed. The third aspect concerns the fact that the methodology is generally simpler and faster to apply than the approaches cited above.
The proposed approach is hierarchical (Fig. 4). The first stage of the uncertainty estimation involves the rasterization of the original 3D geological model consisting of mesh surfaces (the boundaries of lithostratigraphic units and faults) and its representation as a voxel-based volumetric model. Subsequently, the uncertainty of the determination of the rock type is calculated for each voxel, followed by the uncertainty of the determination of the location of faults and, finally, the determination of the general uncertainty (which increases with depth). The combined uncertainty determined from these three sources is then decreased with proximity to the available data sources (boreholes, geological/geophysical profiles and other data sources).
The purpose of such relative uncertainty calculation and visualization is not to improve the process of geological modelling, because the experts creating a geological model should be aware of its uncertainties thanks to their deep knowledge of model input data and manual model construction process. It is rather intended to enhance further practical use of the finished geological models in subsequent works, without the need of deep study of reports accompanying models and the model input data.
The calculation of relative uncertainty presented in this manuscript is quite a new approach that is being applied in practice just in recent several years. The reason for developing and publishing this methodology is the absence of any similar solution that could be applied for our geological models and the common request of our customers to get a semiquantitative uncertainty measure that varies across the volume of each of our models, which they could relatively easily use for further evaluations and decision making.
This study also presents the application of CGS methodology for quantifying the uncertainty of geological models of regions with low levels of input data density in geologically complex areas, using the example of the Čertovka site in the Bohemian Massif, which comprised one of the potential locations for the construction of the Czech deep geological repository for high-level radioactive waste and spent nuclear fuel.
Next section presents the geological situation of the Čertovka case site and a 3D geological model of the site. Another section provides a description of the CGS methodology. The results obtained for the case site are described and discussed in next sections. Finally, key conclusions of the study are provided in the final section.
Geological settings of the pilot test area, 3D geological model and the data for testing the methodology
We selected a 3D geological model of the Čertovka site located in the western part of the Bohemian Massif in central Europe (Fig. 1a and b), with dimensions of approx. 12.2 × 10.4 × 1.5 km as the pilot area for the testing of the methodology for the determination and visualization of the uncertainty of the model. This model was selected due to its high degree of variability in terms of the geological structure and its relatively good coverage by the available archived data, which was of variable quality. The model was used for the initial hydraulic numerical simulation of groundwater flow over a time scale of 106 years created for long-term safety analysis purposes and for planning of field geophysical research. An improved version of the model was subsequently used for the initial design of extensive underground excavations at a depth of ca. 500 m below the surface, including an inclined access tunnel.
(a) Principal units of the Variscan orogenic chain at the European scale. RH, Rhenohercynian Zone; SX, Saxothuringian Zone; MO, Moldanubian Zone. (b) Simplified geological map of the Bohemian Massif modified after Franke (2000), including the location of the study area. (c) Geological map of the study area - top of the analysed 3D geological model. Number of lithostratigraphic items in the legend is higher than 12 mentioned in text, because some lithologies were entirely omitted during voxelization due to too small size of the respective rock bodies
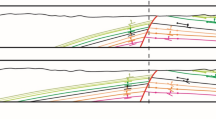
The 3D geological model comprised a total of 12 lithostratigraphic units. The area is located along the western metamorphosed margin of the Teplá-Barrandian Zone, which consists of a several km thick sequence of folded schists and metagreywackes of Neoproterozoic age. The Tis granite pluton of Ordovician age (Dallmayer and Urban 1994) intruded into these metasediments and formed a homogeneous rectangular body with dimensions of approx. 4 × 9 km and a current thickness of approx. 3 km consisting of coarse-grained biotite granite. The body exhibits partially preserved intrusive contact with a contact-metamorphic halo in the west and south, while its eastern boundary is faulted (Žáček 1994). The neighbouring small finger-shaped Lubenec Pluton, presumably of similar age, consists mainly of medium-grained biotite granodiorite to granite with various degrees of deformation (Breiter 2004).
The whole of this sequence underwent limited Variscan metamorphism and deformation and was subsequently covered by the terrestrial clastic sedimentary sequence of Permocarboniferous age (Žáček 1994). In the context of the post-orogenic extension of the Variscan Orogenic Zone, sedimentation spaces, now known as the Manětín, Žihle and Kladno-Rakovník basins, were created due to the increasing subsidence of large areas in the central and western parts of the Bohemian Massif during the late Carboniferous to early Permian. The origin and development of these pull-apart basins were controlled by strike-slip movements along the NW-SE trending fault structures and synchronous normal movements along the N-S oriented faults (Pašek and Urban 1990; Pešek et al. 2001).
The small volcanoes and intrusions of olivine nephelinite in the Tis granite pluton and volcanic rocks in the NW part of the model are related to intraplate basic volcanism in the Cenozoic era (Ulrych et al. 2003).
According to available archival maps and data, the modelled region is crosscut by several significant fault zones and numerous less important faults from numerous episodes of brittle tectonic activity. These faults were classified according to Anderson et al. (2000) in the form of 3 categories based on their lengths on the current surface of the Earth and their estimated thicknesses.
The analysed 3D geological model comprises meshes (TINs) that represent the fault planes and the boundaries of the rock bodies (Fig. 1c). The model was created in MOVE geological modelling software (Petroleum Experts Ltd.) [W1], IPM software suite, and was sliced into 13 horizontal sections at 100 m vertical intervals ranging from − 900 to + 300 m a.s.l. (Fig. 2). Concerning the upper 100 m intervals (14th to 16th between 400 and 600 m a.s.l.), reached only by higher parts of the terrain, the rock bodies and faults were taken from the geological map of the surface. The 2D horizontal sections contain rock type polygons and fault lines that were topologically corrected using ArcMap software [W2] and subsequently rasterized into the form of 2D grids with a cell size of 50 × 50 m (Fig. 3). Hence, with the exception of the non-uniformly thick surface layer, each resulting voxel had dimensions of 50 × 50 × 100 m. This voxel size was selected manually with respect to the size of modelled lithological bodies, the size of the model and its real accuracy given by the scale of the geoscientific input data.
The 3D uncertainty grid of 100 × 100 × 100 m created, including the area of the assumed potential location of the deep geological repository, had total dimensions of 12.2 × 10.4 × 1.5 km.
Research methodology
The proposed approach is hierarchical (Fig. 4). The input for the creation of the uncertainty 3D grid comprised the original 3D geological model as represented by mesh surfaces (the boundaries of the lithostratigraphic units and fault planes) subsequently rasterized and presented as a voxel-based volumetric model. The uncertainty of the determination of the rock types was subsequently calculated for each voxel, followed by the uncertainty of the determination of the course of faults and, finally, the determination of the general uncertainty (which increases with depth). Following the merging of these three types of uncertainties, the total uncertainty decreased with increasing proximity to the spatial geoscientific input data sources (boreholes, geological/geophysical profiles and, possibly, other data sources).
In the case of low amounts, the significantly variable density and/or the significantly variable quality of the geoscientific input data, it is impossible to create a 3D geological model at a sufficient level of quality via the implicit modelling approach, which involves the extensive application of interpolation, automation and geostatistical methods. In such cases, the best results are provided via the manual explicit construction of geological models involving close cooperation between modellers and geologists with extensive field experience of the modelled region. Since the creation of these models is more time consuming and costly, only one model is usually constructed that best fits the available data and broader geological interpretations and theories.
Uncertainty due to local lithological complexity
To quantify the uncertainty stemming from lithological complexity, we adopted a principle previously detailed in various studies, including work by Wellmann and Regenauer-Lieb (2012) for 3D models and by Brus (2014) for 2D applications. The voxelized model is used for this calculation step, where each voxel contains one lithology, that is present in the model at X, Y, Z coordinates of the voxel’s center. We chose spatial entropy, H(S), as an indicator of uncertainty regarding the locations of rock body boundaries and lithological complexity, as entropy has proven effective in prior geological modelling studies as a measure of uncertainty (e.g. Bianchi et al. 2015; Schweizer et al. 2017; Boyd et al. 2019). Using entropy has been validated as a beneficial approach for quantifying and visualizing uncertainties in comprehensive 3D geological models (Wellmann and Caumon 2018).
Brus (2014) points out that the originator of entropy, C.E. Shannon (Shannon and Weaver 1949), defined it for a system with a finite number of possible states S∈{s1,s2,…,sn} and probabilities of occurrence P(si), with information entropy described as:
As explained by Wellmann and Regenauer-Lieb (2012), entropy’s minimum value is zero since log 1 = 0 and \(\:\underset{x\to\:0}{\text{lim}}(x\text{log}x)=0\) (which can be proved using L’Hôpital’s rule, as noted by Ben-Naim (2008). The logarithmic base is adaptable depending on the unit of information chosen; in our case, we used the natural logarithm.
Consequently, information entropy reaches its minimum when all probabilities P(si) are zero except for one, which is equal to 1. Thus, the condition H(Smin) = 0 holds only if ∃ P(sk) = 1 and P(si) = 0 for ∀i≠k, i = 1,2,…,n.
It can also be demonstrated that entropy achieves its maximum when the probabilities of all exclusive states are equal, resulting in a uniform distribution:
This scenario occurs when P(si) = 1/n for every si. Here, entropy reaches its maximum at ln(n) and decreases toward zero as the information content grows, reflecting an inverse relationship between entropy and the amount of information. Entropy represents the average amount of information needed to elimination of uncertainty among a finite set of mutually exclusive cases (in this context, the distinct rock types).
The information entropy computed through Eq. (1) represents a modified Shannon index (as per Jenness et al. 2011; cited in Brus 2014), which can vary from 0 to ln(n) where n indicates the number of unique categories, or rock types in the processed geological model. To normalize uncertainty within a range of 0 to 1, we divide the calculated entropy by ln(n), allowing for a standardized measure of uncertainty across different datasets.
With respect to geological models, the calculated entropy can be interpreted as the amount of missing information, or uncertainty, taking into account the discrete cell properties (stated for 2D by Brus (2014) and for 3D by Wellmann and Regenauer-Lieb (2012). The geological significance of this approach stems from the limited ability of geoscientific methods to precisely identify the extent and boundaries of lithostratigraphic units. The calculation reflects the fact that the greater the number of lithostratigraphic units is present in a small volume (around one voxel), the less precise is the determination of their mutual boundaries, i.e. due to the Quarternary / vegetation cover, which renders geological mapping more difficult on the surface, the ambiguity of geophysical data obtained from depth, etc. The degree of uncertainty defined in this way ranges from 0 (very credible parts of the model) to 1 (very uncertain parts of the model).
The input data for the calculation of uncertainty due to local lithological complexity comprises the 3D grid of the rock types of the geological model. In our case, the grid was created via horizontal slicing in MOVE software and subsequent rasterization in ArcMap software, as described in the previous section.
To determine the uncertainty within each voxel of the 3D geological model, a calculation is performed using a defined voxel neighbourhood within a spherical search space, according to the specified Eq. (1) above. This neighbourhood consists of a set containing N voxels, each with centres positioned within the sphere, which has a user-defined radius. The “user-defined radius” parameter should be set higher than size of a voxel, to include surrounding voxels. The sphere’s centre aligns with the voxel being evaluated for entropy and corresponding uncertainty. For each rock type si present in the neighbourhood, probability P(si) = ni/N is derived by dividing the count of voxels ni containing rock type si by the total N voxels within the defined space. To account for the increase in uncertainty with depth—reflecting the generally reduced reliability of geological interpretations at greater depths - the radius of this spherical neighbourhood is expanded progressively as depth increases to account for less precise location of modelled lithological boundaries at depth compared to Earth surface.
A visual representation of the uncertainty within the geomodel, based on rock types specific to the pilot site, is provided in Fig. 5.
Uncertainty due to the presence of faults
Uncertainty concerning the presence of faults is determined by measuring the distance between the voxels being evaluated and the voxel-based representations of fault planes. Within the geological model for the Čertovka site, we classified three distinct categories of brittle tectonic features. These categories were established according to their length and geological significance, as outlined by Anderson et al. (2000). This classification aids in refining the spatial uncertainty calculations by prioritizing fault types that differ in size and structural importance:
-
1.
Regional fracture zones, length > 10 km, width > 100 m,
-
2.
Local major fracture zones, length 1–10 km, width 5–100 m.
-
3.
Local minor fracture zones, length 10 m-1 km, width 0.1–5 m).
The voxelized model is again used for this calculation step, where each voxel contains either NaN value if no fault crosscuts it, or the highest category of the faults that crosscut the voxel. The approach for calculating uncertainty due to faults differs significantly from that used for lithological uncertainty. The input data for the calculation of the uncertainty of faults comprises the 3D grid of the fault plane types of the geological model. This grid was, again, created via horizontal slicing in MOVE software and its subsequent rasterization in ArcMap software, as described in second section. The head geologist and/or the modeller defines the distance of influence from the fault on the Earth’s surface and the distance of influence from the fault at the base of the model. Concerning the Čertovka test site, this distance was defined by a geologist for each category of faults as ranging from 250 m on the Earth’s surface to 550 m at the base of the model. However, the distance can be defined individually for each fault provided that geoscientific data of a sufficient quality is available. The geological meaning of the distance of influence from the fault concerns the estimate of the thickness of the fault, including the potential extent of the fault deformation zone (the expected extent of significant amounts of smaller-scale brittle structures genetically related to the fault).
In addition, due to the often imprecise determination of the location of faults, a fault location uncertainty value is defined at the uppermost level (on the Earth’s surface), and a higher fault location uncertainty value is defined at the lowest level (the bottom of the model) due to the often unknown or uncertain nature of the dip. Both values range from 0 (very precisely known, i.e. zero uncertainty) to 1 (very imprecisely estimated, i.e. uncertainty 1). These two values are also manually set by the head geologist and/or by the modeller according to their experience from fieldwork in the modelled area and near surroundings and from detailed study of archive materials including geological maps. With respect to our case study, the values were ascribed according to the category classification since the smaller the fault, the more difficult is its identification and the determination of its precise location using geoscientific techniques; hence, category 1 was accorded the lowest location uncertainty and category 3 the highest.
The fault location uncertainty expresses how precisely the fault is located on or near the Earth’s surface and how well its dip can be determined from the available data. This largely depends on the topography, degree of exposure, post-tectonic sedimentary cover, the quality of the geophysical data available and a range of other geoscientific attributes that are related to this parameter since, in practice, they cannot usually be precisely quantified.
The value of the uncertainty of the presence of a particular fault for a particular voxel of the 3D grid is then determined according to the Z coordinate of the voxel as the weighted linear average of the fault location uncertainty values at the uppermost and lowest model levels (i.e. on the Earth’s surface and at the base of the model) in the case that any type of fault is located within the radius of influence (the radius of influence is determined according to the Z coordinate of the voxel as the weighted linear average of the specified distances at the uppermost and lowest levels). The model utilizes a 3D fault grid to identify the specific fault types within each voxel neighborhood. If multiple faults exist within the examined neighborhood, the voxel is assigned the highest uncertainty value associated with any fault present.
A visualization of the uncertainty of the geomodel determined based on the presence of faults at the pilot site is shown in Fig. 6.
General uncertainty calculation
Further, the general uncertainty (the minimum uncertainty that intensifies with depth) is computed. This value is based on parameters provided by the geologist’s expert judgment. These parameters are, admittedly, difficult to estimate; in most cases, 2–3 iterations of the uncertainty calculation are required so as to attain values that are “reasonably” distributed in the whole < 0; 1 > normalized range.
The general uncertainty value quantifies the inherent uncertainty that arises when detailed subsurface exploration is limited. This includes factors such as overlooked (usually smaller) faults or overlooked smaller rock bodies, ambiguous lithological boundaries, indistinct rock formations difficult to differentiate using standard mapping or exploration techniques, and other issues like interpretative ambiguities in shallow geophysics. Such objects, particularly when occurring completely below Earth surface, are often hard to impossible to determine, thus the general uncertainty reflects possibility of their occurrence in real nature while they are missing in the model or the other way round. The level of inexactness is often more or less “constant” throughout the particular areas of the modelled region that have been spatially defined according to the extent of previous exploration and research projects. The general uncertainty is, thus, not related to the modelled lithostratigraphic units or faults, rather it serves to summarise the general quality of the geoscientific data available in the modelled area. In some cases, parts of the modelled area are covered by more detailed geological mapping due e.g. to ore/oil prospecting and the associated drilling campaigns than other parts that are covered merely by regional-scale geological maps. In such cases, it is possible to input the general uncertainty via two numerical parameters (values for the Earth’s surface and for the base of the model) ranging from 0 to 1 for those horizontal polygons allowing us to distinguish surface regions with generally better or poorer data coverage, reflecting variations in archive geological map quality and the geological complexity of the area under study. Such user defined input polygons must in all cases cover the whole horizontal extent of the geological model, without any overlap. If such differentiation is not possible, then the general uncertainty must be defined as being uniform across the whole of the modelled area.
The general uncertainty is calculated for each voxel of the 3D model. Concerning the Earth’s surface and the base of the model, values are assigned by the head geologist, whereas the volume in between is linearly interpolated. A visualization of the general uncertainty of the geomodel of the pilot site is shown in Fig. 7.
Calculation of the total uncertainty and the reduction of uncertainty near to data sources
The three key uncertainty types—lithological, fault-related, and general—are then integrated. Although it is possible to simply sum these uncertainty values for each voxel (capped at a maximum of 1), combining them through fuzzy logic is considered more robust method.
Fuzzy logic, originating from Zadeh’s fuzzy set theory (Zadeh 1965), assigns a degree of membership (often a real number between [0, 1]) to elements in a set, allowing a range of truth values from total falsehood (0) to absolute truth (1). In fuzzy logic, this degree of truth corresponds inversely to uncertainty, creating a continuous scale of intermediate truth values (Cintula et al. 2023).
In applying fuzzy logic to uncertainty in geological modelling, the standard Gödel fuzzy conjunction (t-norm) is used, where the truth degree of combined statements reflects the minimum truth degree of individual inputs (Bělohlávek et al. 2017; Cintula et al. 2023). When adapted to uncertainty, this method yields the highest uncertainty value among lithological, fault-related, and general uncertainties.
For comparison purposes, Figs. 8 and 9 present visualizations of the total uncertainty of the geomodel of the pilot site as determined in each voxel via the two above approaches. The total uncertainty in Fig. 8 was determined via the sum of the lithological, fault and general uncertainties (with a maximum value limit of 1), whereas the total uncertainty of the geomodel in Fig. 9 was determined by the maximum of the values of the lithological, fault and general uncertainties (based on the fuzzy logic principle).
Finally, the reduction in the already calculated total uncertainty (increase in credibility) value with respect to the vicinities of geoscientific data sources used to construct the geological model is determined. This final step is introduced so as to include the positive impact of the existing data (input for the construction of the model) on the credibility of the model. Borehole and geological section data was available for the Čertovka test site; however, the same principle applies to other types of spatial input data (geophysical profiles, structural measurements etc.).
With concern to all this data, the user must enter the respective geographical positions and the expert estimation of the quality of the data, for example in the form of a 2D point (e.g. for boreholes or structural measurements) / line (e.g. for various geophysical or geological profiles) / polygon (defining regions of different general uncertainty) SHP file format, as well as the depth extent, reliability estimate in percent and “impact radius” parameters, in the corresponding attribute table. We have decided to measure the degree of reliability of the input data provided by an expert by percentages, because of its simplicity and ease of use.
The percentage reduction of uncertainty of boreholes decreases linearly in a specified radius from the borehole path, concerning which the uncertainty reduction is decided by the user towards the circumference of the cylinder of influence within a radius that is determined around the borehole, where the uncertainty reduction is zero.
In the case of geological and geophysical (vertical) sections, the uncertainty reduction percentage decreases linearly from the (vertical) section area, where the percentage estimate of the accuracy and precision of the section is given, to the user-defined distance from the section, where the uncertainty reduction is zero. In principle, the same approach can be applied to point data such as the structural measurements of foliation planes on rock outcrops; the highest uncertainty reduction is applied to the outcrop locations and it decreases spherically around these points.
It is necessary that the user defines these distances since none of the above calculations are able to take into account the structural complexity (the cylindricity of ductile deformations and their intensity, the type, style and interference of deformations or the magnitude of movements along the most prominent faults etc.), which exerts a profound impact on the explanatory power of the input data in the neighbourhood of the geoscientific input data.
The corresponding calculation initially involves the multiplication of the total uncertainty in each voxel by the sum of the increase in credibility (in percent) of all the geoscientific data input values (provided they are present in vicinity of the calculated voxel - in the case of the Čertovka test site two sources of geoscientific input data were available - boreholes and geological sections). The resulting value is then divided by 100 and this value is then subtracted from the original total uncertainty value. This approach is applied so as to reduce the uncertainty values in the proximity of geoscientific input data sources for each voxel of the 3D uncertainty grid of the geological model. Each of the voxels of the output 3D grid for the Čertovka site contained both the resulting scalar uncertainty value and the values determined from the individual calculation steps, since it was thought that the latter could have a similar value for certain follow-up applications as the total resulting uncertainty value itself.
Figure 11 shows a visualization of the total uncertainty of the geomodel using ScatterPlot (top) and Isosurface - an envelope with a relative uncertainty value of 0.3 (bottom).
Evaluation of the results
This section refers to the application of the procedures described in the previous section to the geological model of the Čertovka site. The visualizations were created in the Voxler environment [W3].
The calculation parameters below were chosen with respect to the size of the model, size of modelled rock bodies and the density of the voxels.
Uncertainty due to the local lithological complexity - Čertovka site
The input data comprised a grid of the rock types on the surface and grids of the rock types in the individual horizontal slices of the geological model, which were created at 100 m intervals (from − 900 m above sea level to immediately below the surface). The grid resolution was 50 × 50 m. The resulting 3D grid of the lithology was used to calculate the 3D uncertainty grid in view of the local lithological complexity at a resolution of 100 × 100 × 100 m. The number of rock types (n) = 12.
In order to account for the increase in uncertainty with depth, the radius of the evaluated spherical environment was expanded with increasing depth from 150 m at the surface to 350 m at the lowest level of the model.
Figure 5 shows a visualization of the uncertainty of the geomodel determined based on the rock types.
Uncertainty due to the presence of faults - Čertovka site
The input data comprised a grid of fault types on the Earth surface and grids of fault types in the individual horizontal slices of the geological model, which, as with the grids of the rock types of the individual layers of the geological model, were created at 100 m intervals (from − 900 m above sea level to immediately below the surface). The horizontal resolution of the grids was also 50 × 50 m. The resulting 3D fault grid was used to calculate the 3D uncertainty grid due to the occurrence of faults at the same resolution of 100 × 100 × 100 m.
The head geologist determined the distance of influence from the faults on the Earth’s surface at 250 m and the distance of influence from the faults at the base of the model at 550 m according to the three defined fault categories.
The uncertainties of the fault location uncertainty values at the uppermost level were entered for fault categories 1, 2 and 3 as 0.1, 0.15 and 0.4, respectively, and the uncertainties of the fault location uncertainty values at the base level for fault categories 1, 2 and 3 as 0.2, 0.5 and 0.9 respectively.
Figure 6 shows a visualization of the uncertainty of the geomodel determined based on the occurrence of faults.
Calculation of the general uncertainty – Čertovka site
The general uncertainty was calculated for each voxel of the geomodel at the same resolution of 100 × 100 × 100 m. The head geologist defined (for the entire area) a basic general uncertainty value on the Earth’s surface of 0.1 and at the base of the model 0.35. In addition, he defined three polygons with differing parameters, based on extent of geologically more complex areas insufficiently covered by higher-resolution geological maps:
-
1.
general uncertainty on the Earth’s surface of 0.3 and at the base of the model 0.5 (top right in Fig. 7),
-
2.
general uncertainty on the Earth’s surface of 0.4 and at the base of the model 0.65 (top left in Fig. 7),
-
3.
general uncertainty on the Earth’s surface of 0.5 and at the base of the model 0.7 (bottom right in Fig. 7).
The rest of the modeller area was given general uncertainty on the Earth’s surface of 0.1 and at the base of the model 0.35.
These parameters reflect both objective and subjective sources of uncertainty in the particular areas, which were identified based on extensive fieldwork and the study of the available data and literature.
Figure 7 shows a visualization of the general uncertainty of the geomodel.
Calculation of the total uncertainty and the reduction of uncertainty around data sources - Čertovka site
This section described two approaches to combining the three differing sources of uncertainty (lithological, fault and general) so as to determine the total uncertainty:
-
Simple addition with a limit of 1 (maximum uncertainty) – Fig. 8,
-
The maximum of the lithological, fault and general uncertainty values (based on the fuzzy logic principle) - Fig. 9.
A comparison of Figs. 8 and 9 confirmed that the second method was more appropriate, hence this approach was applied in practice.
In conclusion, a reduction in the total uncertainty value (increase in credibility) was applied to the vicinities of the geoscientific data sources used in the construction of the original geological model. The Čertovka site featured 510 mostly shallow boreholes and two geological sections. Given the resolution of the resulting 3D grid (100 × 100 × 100 m) and the specified radius from the borehole axes (50 m), these shallow boreholes did not exert a significant impact on the reduction of the total uncertainty. Figure 10 shows the percentage reductions in total uncertainty due to the boreholes and sections according to the user-specified parameters. Figure 11 shows a visualization of the total uncertainty of the geomodel following the reduction of the uncertainty around the boreholes and sections.
The resulting 3D uncertainty grid can be connected to the geological model using modelling software (e.g. MOVE, which is used by the Czech Geological Survey). The total uncertainty values are plotted in MOVE in the form of points, and size- and colour-scaled according to the uncertainty value. The second option concerns exporting the IsoSurface for several levels of uncertainty from the Voxler program. Figure 12 provides an example of the resulting compilation of a geological model with an IsoSurface of uncertainty for a value of 0.35. The areas of low uncertainty can easily be identified, as can the areas in which more detailed geological exploration should be conducted for the potential siting of the deep geological repository.
The resulting compilation of the geological model with an IsoSurface of uncertainty of 0.35 for the Čertovka site, including the input geoscientific data – boreholes and geological sections. Yellow plane near model centre marks a preliminary suggestion of the underground repository location at 500 m depth
Discussion
The described procedure is intended for the practical use of uncertainty calculations in situations where only one explicit geological model is created manually; for which it is then necessary to determine the degree of uncertainty for the subsequent use of the model for other applications. Typically such models comprise crystalline massifs exhibiting polyphase metamorphic, magmatic and deformation history, that lack any extensive and detailed geoscientific dataset stemming from previous exploration works. Such a situation, moreover partly covered by Quarternary accumulations and soils and/or heavily obscured by vegetation occurs very often e.g. in the Czech Republic, from which the example model was chosen.
Such geological models are usually created at the CGS manually in the MOVE software environment. In addition to the available geoscientific spatial input data, the experience of the responsible geologists, who apply their own interpretations assuming a certain tectonic regime(s) and are aware of history of geological research in the modelled area and its surrounding regional geological units, plays a significant role in the stepwise model construction process.
In the case of low amounts or the significantly variable density and quality of the geoscientific input data, the manual creation of just one model rules out the application of classic uncertainty calculations based on the comparison of range of (semi-) automatically created models. No suitable uncertainty calculation methodology has yet been published for such cases, so that the presented methodology fills this gap. Moreover, it allows for the variant setting of the input parameters for the implementation of specific geological models.
It is clear that the specific values of the resulting 3D uncertainty grid are dependent on the expert setting of the input parameters by the user. These values significantly impact all steps of the calculation - of the lithological, fault and general uncertainty and the reduction in the value of the total uncertainty in the vicinity of the geoscientific data sources used in the construction of the geological model. This subjectivity nevertheless cannot be excluded due to heterogeneous and generally unknown quality of the archival input data and the manual and thus subjective modelling process, relying on the expertise of the geologists and modellers in charge.
3D grid form of representation of the uncertainty values was chosen due to versatility of such approach to describe variable parameters across a volume of interest, and ease of import and export of 3D grids or voxels to various sw. tools. User selection of voxel size for the model discretization and uncertainty grid cell size also affects the results of the uncertainty calculation. Their size should be chosen with respect to size of the geological model and detail which the model depicts (in 2D equivalent to scale or detail of a geological map), to allow for representation of majority of the modelled faults and lithological boundaries in the voxelized form of the geological model.
The authors’ selection of several constituents of the final uncertainty arise from common types of objects that the geological models are made from – boundaries of lithological, resp. lithostratigraphic bodies, and fault planes, resp. planes of brittle structures. Despite a fraction of the lithological boundaries is faulted, i.e. represented by fault planes, majority of them is often unrelated to significant faults and thus representing genetically different surfaces that are identified by different indications from the geological and geophysical data. Importance of lithological or lithostratigraphic boundaries and of fault planes for further use of the geological models is also significantly different. For all these reasons these two types of objects are treated separately. As lithological bodies fill the whole model volume, but fault planes are present just in a small fraction of the model volume, each of them is solved by different calculation process during our uncertainty assessment.
For lithological uncertainty, the use of spatial entropy was the only choice, as the use of entropy has been validated as the most beneficial approach for quantifying and visualizing uncertainties in many complex 3D geological models (e.g. Bianchi et al. 2015; Schweizer et al. 2017; Boyd et al. 2019) and as it is suitable for 3D grids in which each cell (voxel) contains data (no NaN values are present).
In contrast, the calculation of uncertainty related to faults is determined by the distances between the evaluated voxels and the representations of fault planes in the geological model. In doing so, different categories of brittle tectonic features are classified. These categories are determined according to their length and geological significance. This classification helps to refine the calculations of spatial uncertainty by prioritizing types of faults that differ in size and structural importance. Due to numerous voxels containint NaN values (i.e. without any fault plane crosscutting them), the above mentioned information entropy cannot be used in this case.
The introduction of the so-called general uncertainty may seem redundant or overlapping with the two above mentioned uncertainty constituents, but neither is true. It is necessary to account for real natural heterogeneity of rock environment vs. rapid decrease of geoscientific data available with increasing depth. If a general uncertainty would not be introduced, then e.g. a hypothetic model consisting of just one rock body without any fault would exhibit uniform uncertainty across whole modelled volume, while the uncertainty at depth of the model must be of course higher than at surface because much less data (if any) is known from the depth then from a surface research, mapping and/or exploration. Even such simple surface geology in the input data would not be a guarantee of same simplicity at depth of the rock massif.
Our methodology is quite new, so that only several examples of its application can be given so far.
Presently this uncertainty was evaluated in geological models of crystalline units that Czech Geological Survey was creating for initial planning phases of extension of both nuclear powerplants located in Dukovany and Temelin in the Czech Republic. The resulting uncertainty values were exported as a non-graphical property of voxels in a voxelized geological model of the rock environment at both future construction sites. The voxels were then exported to BIM IFC format (ISO 16739-1 (2024), having the uncertainty value stored as a real-number property of each voxel, and combined with other geological, hydrogeological, engineering geological and initial designers BIM models to integrate all the available geoscientific information for the powerplants’ operator company. The operator uses it presently for more detailed planning of the future constructions, for formulation of geological and geotechnical parts of contracts for the powerplants’ extension and extremely expensive works, particularly for optimalization of rough landscaping, siting of subsurface parts of buildings, safety assessment including fulfilling of strict criteria of Czech State Office for Nuclear Safety, planning of further stages of geological and geotechnical exploration and sampling and risk management related to all of the aforementioned works. Particularly the location of additional exploration works should be then focused on rock volumes, which exhibit high values of the relative uncertainty in the vicinity of planned larger constructions such as reactor buildings and turbines. Such approach leads to exploration optimization to decrease both – cost of further exploration works and construction costs to mitigate unfavourable unexpected geology and thus also reducing risk during construction and also during production stage of the two powerplants.
Such uncertainty calculation was presently adopted also for a voxel-based geotechnical model of a construction site, where the different geotechnical categories of rocks and soils were treated in the uncertainty calculation as different lithologies, resulting in an ucertainty distribution across a geotechnical model.
Similar approach is presently being developed in cooperation with the Czech Radioactive Waste Repository Authority, where more complex approach is necessary, because the related safety assessment must reach cca. 1.000.000 years to the future. Such application includes uncertainty propagation from initial geological models through following 3D numerical models of groundwater flow and simulations of transport of radionuclides, which is presently just in initial stages of development.
All the above mentioned examples is unfortunately not possible to publish due to contract restrictions, so that we present a pilot uncertainty study of the Čertovka abandoned potential locality for spent nuclear fuel, where a permission to publish our results was kindly provided by the Czech Radioactive Waste Repository Authority.
In both cases above, the target group of users of the uncertainty are experts in charge, who have neither deep geological education nor extensive fieldwork and archive material research experience from the region around evaluated localities, nevertheless their work relies on siting of strategically important and expensive constructions into complex rock environment. In these cases the relative uncertainty calculations well serve for translation of variably uncertain heterogeneous geoscientific input data and variably uncertain geological model to simple real numbers that can be easily compared by a designer, engineer etc. across a single model or among several models created by similar methodology.
If the geological model is validated / updated using newly acquired field geological or geophysical data, then the uncertainty can be calculated again using the spatial distribution and other parameters of the new input data together with the new geological model as the calculation inputs. Then the uncertainty distribution across the voxelized new model will naturally reflect the new data, including uncertainty decrease in the vicinity of the input data coming from new field exploration.
A question remains how the validity of our uncertainty quantifications can be demonstrated, especially when the results are not accepted at face value, without validation measurements and probabilistic guarantees. We believe that currently these are impossible, due to many subjectively defined input calculation parameters.
Future research must therefore focus on designing and testing a potential validation approach. This could be possible with use of a precise („calibration“) geological model with properties typical for the localities that we study. This model would be artificially created for this purpose and considered as a model without uncertainty.
An expert geologist would manually create a geological model of the same locality, based on a limited input borehole data or geophysical profiles, generated from the calibration model, in realistic quantity and spatial distribution, typical for real-world situations, thus of similar properties to the data of the Čertovka area. Based on this geological model, the 3D uncertainty grid would be created through the CGS methodology. This 3D uncertainty grid would subsequently be used to compare the manually created geological model with the calibration model, through visual and quantitative assessment.
Gradually, one could compare areas created according to individual boundary values for uncertainty (e.g., from 0 to 0.1, from 0.1 to 0.2, …, from 0.9 to 1) and potentially also separately for brittle structures and lithological boundaries for regions with a high uncertainty. If the differences in rock types and faults between the manually created geological model and the calibration model would not correspond to the uncertainty calculated through the CGS methodology (e.g., from 0 to 10%, from 10 to 20%, …, from 90 to 100%), the input parameters for the uncertainty calculation would need to be adjusted so that the difference would become acceptable.
Conclusions
This paper provides a description of a novel methodology for estimating and visualizing the relative uncertainty of geological models of regions with low coverage of input geoscientific data in geologically complex areas, as developed by the Czech Geological Survey. The methodology emerged due to the need to quantify the degree of uncertainty of such kinds of models for their subsequent practical use.
Our novel methodology involves the successive determination of the uncertainty of the rock types and the course of faults and the so-called general uncertainty for each voxel of the spatial uncertainty 3D grid, which is of same size as the original geological model. The combined uncertainty determined from these three sources is then reduced in the proximity of available input data sources. Thus, a 3D uncertainty grid is created relatively quickly and economically based on just one explicit geological model.
The calculated uncertainty scalar values, normalized within the range of < 0; 1>, do not possess a precise quantitative significance. This limitation primarily arises from the diverse nature of the input data and the numerous expert estimations required to define the calculation parameters. Moving forward, we recognize the challenges in developing a universal method to establish absolute uncertainty values for 3D models of geologically intricate terrains, especially in regions with relatively sparse available geoscientific data. Nevertheless, our methodology provides useful metrics for comparing relative uncertainty across different sections of independent geological models. If a uniform approach to the input parameters preparation is applied, then the presented methodology can also be used to compare the relative uncertainty across a single generation of several methodologically uniform models (for example, for the study of several potential sites for the construction of the Czech deep geological repository for high-level radioactive waste and spent nuclear fuel).
These uncertainty values are specifically intended for users without a strong geological background or detailed regional geological knowledge, who may otherwise lack insight into the uncertainties present within these models. Due to many subjective input parameters based on expert estimates, the resulting uncertainty values must be treated with caution. Key users of this data include professionals involved in large ground or underground construction engineering, such as engineers and designers of tunneling and opencast / underground mining projects, experts in geotechnical analysis and in geomechanics or hydraulic modeling teams specializing in groundwater flow. This approach is consistent with the Czech Geological Survey’s previous work in enhancing accessibility and reliability of geological information for non-geologist users. The 3D grid of relative uncertainty that is created via the presented methodology can be simply imported into various 3D software tools together with the 3D geological model and with third-party 3D excavation, exploration or construction plans so as to e.g. determine areas in which more detailed exploration work should be conducted prior to the start of construction work, or where particular care must be taken during the design stage without the need to study extensive geoscientific input data and the related geological literature.
Data availability
No datasets were generated or analysed during the current study.
References
Amarante FAN, Rolo RM, Costa JFCL (2019) Assessing geologic model uncertainty - a case study comparing methods. REM Int Eng J 72(4):643–653. https://doi.org/10.1590/0370-44672019720037
Anderson J, Grundteknik G, Strom A, Svemar C, Almén KE, Ericsson LO (2000) Technical report TR-00–12 – What requirements does the KBS-3 repository make on the host rock? Geoscientific suitability indicators and criteria for siting and site evaluation – SKB, Stockholm, Sweden. https://www.skb.com/publication/17609/TR-00-12.pdf. Accessed 14 Nov 2024
Bělohlávek R, Dauben JW, Klir GJ (2017) Fuzzy logic and mathematics: a historical perspective. Oxford University Press, New York. https://doi.org/10.1093/oso/9780190200015.001.0001
Ben-Naim A (2008) A farewell to entropy: statistical thermodynamics based on information. World Scientific, Singapore
Bianchi M, Kearsey T, Kingdon A (2015) Integrating deterministic lithostratigraphic models in stochastic realizations of subsurface heterogeneity. Impact on predictions of lithology, hydraulic heads and groundwater fluxes. J Hydrol 531:557–573. https://doi.org/10.1016/j.jhydrol.2015.10.072
Bond CE (2015) Uncertainty in structural interpretation: lessons to be learnt. J Struct Geol 74:185–200. https://doi.org/10.1016/j.jsg.2015.03.003
Boyd DL, Walton G, Trainor-Guitton W (2019) Quantifying spatial uncertainty in rock through geostatistical integration of borehole data and a geologist’s cross-section. Eng Geol 260:105246. https://doi.org/10.1016/j.enggeo.2019.105246
Breiter K (2004) Granitoidy tiského masivu. Zpr geol Výzk v roce 2003:13–16. Czech. https://app.geology.cz/img/zpravyvyzkum/fulltext/zpravy-o-vyzkumech-2003-str-013-16.pdf. Accessed 14 Nov 2024
Brus J (2014) Vizualizace nejistoty v environmentálních studiích. Univerzita Palackého. Přírodovědecká fakulta, Olomouc. Czech
Cintula P, Fermüller CG, Noguera C (2023) Fuzzy logic. in: the stanford encyclopedia of philosophy (Summer 2023 Edition). In: Edward N. Zalta, Uri Nodelman (eds). https://plato.stanford.edu/archives/sum2023/entries/logic-fuzzy/. Accessed 14 Nov 2024
Cremon MA, Christie M, Gerritsen MG (2018) Monte carlo simulation for uncertainty quantification in reservoir simulation: a convergence study. In: Proceedings of the ECMOR XVI – 16th European Conference on the Mathematics of Oil Recovery. Barcelona: ECMOR, 1–18. https://doi.org/10.3997/2214-4609.201802226
Dallmeyer RD, Urban M (1994) Variscan vs cadomian tectonothermal evolution within the teplá-barrandian zone, bohemian massif, Czech republic: Evidence from 40Ar/39Ar mineral and whole-rock slate/phyllite ages. J Czech Geol Soc 39:21–22. http://www.jgeosci.org/content/JCGS1994_1__021_Dallmeyer.pdf. Accessed 14 Nov 2024
de la Varga M, Schaaf A, Wellmann F (2019) GemPy 1.0: open-source stochastic geological modeling and inversion. Geosci Model Dev 12(1):1–32. https://doi.org/10.5194/gmd-12-1-2019
Franke W (2000) The Mid-european segment of the variscides: tectono-stratigraphic units, terranes, boundaries and plate evolution. In: Franke W, Haak V, Oncken O, Tanner D (eds) Orogenic processes: quantification and modelling in the Variscan Belt, 179. Geological Society London. Special, London, pp 35–61. https://doi.org/10.1144/GSL.SP.2000.179.01.05
González-Garcia J, Jessell M (2016) A 3D geological model for the Ruiz-Tolima Volcanic Massif (Colombia): Assessment of geological uncertainty using a stochastic approach based on Bézier curve design. Tectonophysics 687:139–157. https://doi.org/10.1016/j.tecto.2016.09.011
Guo J, Wang J, Wu L, Zhu W, Jessell M, Li C, Li F, Hu H (2022) Automatic and dynamic updating of three-dimensional ore body models from borehole and excavation data using the implicit function HRBF. Ore Geol Rev 148:105018. https://doi.org/10.1016/j.oregeorev.2022.105018
Guo J, Wang Z, Li C, Li F, Jessel MW, Wu L, Wang J (2022) Multiple-point geostatistics-based three-dimensional automatic geological modeling and uncertainty analysis for borehole data. Nat Resour Res 31:2347–2367. https://doi.org/10.1007/s11053-022-10071-6
Huang J, Deng H, Chen J, Li N, Wang J, Liu Z, Mao X (2023) Assessing geometrical uncertainties in geological interface models using Markov chain Monte Carlo sampling via abstract graph. Tectonophysics 864:230032. https://doi.org/10.1016/j.tecto.2023.230032
ISO 16739-1 (2024) Industry Foundation Classes (IFC) For Data Sharing In The Construction And Facility Management Industries — Part 1: Data Schema, Geneva. https://www.iso.org/standard/84123.html
Jenness J, Brost B, Beier P (2011) Land facet corridor designer: extension for ArcGIS. Jenness Enterprises. https://www.researchgate.net/publication/228787733_Land_Facet_Corridor_Designer. Accessed 14 Nov 2024
Jessell MW, Ailleres L, de Kemp EA (2010) Towards an integrated inversion of geoscientific data: what price of geology? Tectonophysics 490(3–4):294–306. https://doi.org/10.1016/j.tecto.2010.05.020
Jin X, Wang G, Tang P, Hu C, Liu Y, Zhang S (2020) 3D geological modelling and uncertainty analysis for 3D targeting in Shanggong gold deposit (China). J Geochem Explor 210:106442. https://doi.org/10.1016/j.gexplo.2019.106442
Jørgensen F, Høyer AS, Sandersen PBE, He X, Foged N (2015) Combining 3D geological modelling techniques to address variations in geology, data type and density – an example from Southern Denmark. Comput Geosci 81:53–63. https://doi.org/10.1016/j.cageo.2015.04.010
Krajnovich A, Zhou W, Gutierrez M (2020) Uncertainty assessment for 3D geologic modeling of fault zones based on geologic inputs and prior knowledge. Solid Earth 11:1457–1474. https://doi.org/10.5194/se-11-1457-2020
Kuhn S, Cracknell MJ, Reading AM (2019) Lithological mapping in the central African copper belt using random forests and clustering: Strategies for optimised results. Ore Geol Rev 112:103015. https://doi.org/10.1016/j.oregeorev.2019.103015
Lecour M, Cognot R, Duvinage I, Thore P, Dulac JC (2001) Modelling of stochastic faults and fault networks in a structural uncertainty study. Pet Geosci 7(S):S31–S42. https://doi.org/10.1144/petgeo.7.S.S31
Lindsay M, Perrouty S, Jessell M, Ailleres L (2014) Inversion and geodiversity: Searching model space for the answers. Math Geosci 46(8):971–1010. https://doi.org/10.1007/s11004-014-9538-x
Lindsay MD, Aillères L, Jessell MW, de Kemp EA, Betts PG (2012) Locating and quantifying geological uncertainty in three-dimensional models: analysis of the Gippsland Basin, southeastern Australia. Tectonophysics 546–547:10–27. https://doi.org/10.1016/j.tecto.2012.04.007
Liu Y, Zhang X, Guo W, Kang L, Gao J, Yu R, Sun Y, Pan M (2022) Research status of and trends in 3D geological property modeling methods: a review. Appl Sci 12:5648. https://doi.org/10.3390/app12115648
Lyu M, Ren B, Wu B, Tong D, Ge S, Han S (2021) A parametric 3D geological modeling method considering stratigraphic interface topology optimization and coding expert knowledge. Eng Geol 293:106300. https://doi.org/10.1016/j.enggeo.2021.106300
Mery N, Emery X, Cáceres A, Ribeiro D, Cunha E (2017) Geostatistical modeling of the geological uncertainty in an iron ore deposit. Ore Geol Rev 88:336–351. https://doi.org/10.1016/j.oregeorev.2017.05.011
Ouyang J, Zhou C, Liu Z, Zhang G (2023) Triangulated irregular network-based probabilistic 3D geological modelling using markov chain and Monte Carlo simulation. Eng Geol 320:107131. https://doi.org/10.1016/j.enggeo.2023.107131
Pakyuz-Charrier E, Giraud J, Ogarko V, Lindsay M, Jessell M (2018) Drillhole uncertainty propagation for three-dimensional geological modeling using Monte Carlo. Tectonophysics 747–748:16–39. https://doi.org/10.1016/j.tecto.2018.09.005
Pakyuz-Charrier E, Jessell M, Giraud J, Lindsay M, Ogarko V (2019) Topological analysis in Monte Carlo simulation for uncertainty propagation. Solid Earth 10:1663–1684. https://doi.org/10.5194/se-10-1663-2019
Pakyuz-Charrier E, Lindsay M, Ogarko V, Giraud J, Jessell M (2018) Monte Carlo simulation for uncertainty estimation on structural data in implicit 3-D geological modeling, a guide for disturbance distribution selection and parameterization. Solid Earth 9:385–402. https://doi.org/10.5194/se-9-385-2018
Pašek J, Urban M (1990) The tectonic evolution of the plzeň basin (Upper Carboniferous, West Bohemia): a review and reinterpretation. Folia Musei rerum naturalis Bohemiae occidentalis - Geologica 32:1–56
Pešek J, Holub V, Malý L, Martínek K, Prouza V, Spudil J, Tásler R (2001) Geology and Deposits od upper paleozoic basins of the Czech Republic. Český geologický ústav, Praha. Czech, transl. title (Geologie a ložiska svrchnopaleozoických pánví České republiky), pp 1–243. https://www.researchgate.net/publication/39848717_Geologie_a_loziska_svrchnopaleozoickych_limnickych_panvi_Ceske_republiky. Accessed 14 Nov 2024
Pirot G, Joshi R, Giraud J, Lindsay MD, Jessell MW (2022) loopUI-0.1: indicators to support needs and practices in 3D geological modelling uncertainty quantification. Geosci Model Dev 15(12):4689–4708. https://doi.org/10.5194/gmd-15-4689-2022
Sadeghi B, Cohen DR (2023) Decision-making within geochemical exploration data based on spatial uncertainty – a new insight and a futuristic review. Ore Geol Rev 161:105660. https://doi.org/10.1016/j.oregeorev.2023.105660
Schneeberger R, de La Varga M, Egli D, Berger A, Kober F, Wellmann F, Herwegh M (2017) Methods and uncertainty estimations of 3-D structural modelling in crystalline rocks: a case study. Solid Earth 8:987–1002. https://doi.org/10.5194/se-8-987-2017
Schorpp L, Straubhaar J, Renard P (2022) Automated hierarchical 3D modeling of quaternary aquifers: The ArchPy Approach. Front Earth Sci 10:884075. https://doi.org/10.3389/feart.2022.884075
Schweizer D, Blum P, Butscher C (2017) Uncertainty assessment in 3-D geological models of increasing complexity. Solid Earth 8:515–530. https://doi.org/10.5194/se-8-515-2017
Shahri AA, Chunling S, Larsson S (2023) A hybrid ensemble-based automated deep learning approach to generate 3D geo-models and uncertainty analysis. Eng Comput. https://doi.org/10.1007/s00366-023-01852-5
Shannon CE, Weaver W (1949) The mathematical theory of communication. University of Illinois Press, Urbana
Tacher L, Pomian-Srzednicki I, Parriaux A (2006) Geological uncertainties associated with 3-D subsurface models. Comput Geosci 32(2):212–221. https://doi.org/10.1016/j.cageo.2005.06.010
Ulrych J, Lloyd F, Balogh K (2003) Age relations and geochemical constraints of cenozoic alkaline volcanic series in W Bohemia: a review. Geolines 15:168–180
Van Der Grijp Y, Minnitt R, Rose D (2021) Modelling a complex gold deposit with multiple-point statistics. Ore Geol Rev 139(A):104427. https://doi.org/10.1016/j.oregeorev.2021.104427
Veliz V, Maleki M, Madani N, Soltani-Mohammadi S, Mery N, Emery X (2023) Plurigaussian modeling of non-stationary geological domains to assess geological uncertainty in a porphyry copper deposit. Ore Geol Rev 162:105707. https://doi.org/10.1016/j.oregeorev.2023.105707
Wellmann F, Caumon G (2018) Chapter one – 3-D structural geological models: concepts, methods, and uncertainties. Adv Geophys 59:1–121. https://doi.org/10.1016/bs.agph.2018.09.001
Wellmann JF, De La Varga M, Murdie RE, Gessner K, Jessell M (2018) Uncertainty estimation for a geological model of the sandstone greenstone belt, western Australia - insights from integrated geological and geophysical inversion in a bayesian inference framework. Geol Soc Spec Publ 453(1):41–56. https://doi.org/10.1144/SP453.12
Wellmann JF, Lindsay M, Poh J, Jessell M (2014) Validating 3-D structural models with geological knowledge for improved uncertainty evaluations. Energy Procedia 59:374–381. https://doi.org/10.1016/j.egypro.2014.10.391
Wellmann JF, Regenauer-Lieb K (2012) Uncertainties have a meaning: information entropy as a quality measure for 3-D geological models. Tectonophysics 526–529:207–216. https://doi.org/10.1016/j.tecto.2011.05.001
Yamamoto JK, Koike K, Kikuda AT, Campanha GAC, Endlen A (2014) Post-processing for uncertainty reduction in computed 3D geological models. Tectonophysics 633:232–245. https://doi.org/10.1016/j.tecto.2014.07.013
Yang L, Hyde D, Grujic O, Scheidt C, Caers J (2019) Assessing and visualizing uncertainty of 3D geological surfaces using level sets with stochastic motion. Comput Geosci 122:54–67. https://doi.org/10.1016/j.cageo.2018.10.006
Yin Z, Strebelle S, Caers J (2020) Automated monte Carlo-based quantification and updating of geological uncertainty with borehole data (AutoBEL v1.0). Geosci Model Dev 13:651–672. https://doi.org/10.5194/gmd-13-651-2020
Žáček V (1994) Garnets and metamorphic evolution of the teplá crystalline complex. Western Bohemia. Zbl Geol Paläontol Tei I(7/8):847–856
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353. https://doi.org/10.1016/S0019-9958(65)90241-X
References to a website
[W1] petroleum engineering and structural geology software move suite. https://www.petex.com/products/move-suite/. Accessed 14 November 2024
[W2] ESRI About arcGIS. https://www.esri.com/en-us/arcgis/about-arcgis/overview. Accessed 14 November 2024
[W3] golden software, Voxler https://support.goldensoftware.com/hc/en-us/sections/204130867-Voxler. Accessed 14 November 2024
Acknowledgements
This research forms a contribution to the Strategic Research Plan of the Czech Geological Survey (DKRVO/ČGS 2023-2027), which supported much of the development of the methodology and its application to the selected geological model. In addition, support from the GeoERA project, GeoE.171.005 (3D Geomodeling for Europe), is gratefully acknowledged. The 3D geological model for the testing of the methodology was used following kind permission from the Czech Radioactive Waste Repository Authority (SÚRAO). We are grateful to three anonymous reviewers for constructive critics and provoking questions, that led to the improvement of the initial manuscript.
Funding
Open access publishing supported by the institutions participating in the CzechELib Transformative Agreement. This research was partially supported by the Strategic Research Plan of the Czech Geological Survey (DKRVO/ČGS 2023–2027) and the GeoERA project, GeoE.171.005 (3D Geomodeling for Europe).
Author information
Authors and Affiliations
Contributions
Conceptualization: F.S., J.F.; Data curation: J.J.,V.Ž.; Funding acquisition: J.F.; Investigation: F.S., J.F.; Methodology: F.S., J.F.; Software: F.S.; Visualization: F.S., J.F., J.J.; Writing – original draft: F.S., J.F., J.J.,V.Ž.; Writing – review & editing: F.S., J.F., J.J. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Communicated by: H. Babaie
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Staněk, F., Franěk, J., Jelínek, J. et al. Estimating relative uncertainty of geological 3D models with low density of input data in geologically complex regions. Earth Sci Inform 18, 259 (2025). https://doi.org/10.1007/s12145-025-01778-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12145-025-01778-0