Introduction

In the past few decades, climate change and global warming have caused and exacerbated natural disasters (Kadam et al. 2024). Drought ranks among the most severe global natural disasters and is defined as a prolonged precipitation-deficient period that results in inadequate water availability for crops, humans and animals (Mehr et al. 2022). Drought definitions are generally categorized into meteorological, agricultural, hydrological, and socioeconomic definitions (AghaKouchak et al. 2022). Among these, meteorological drought is generally defined as a period of precipitation deficiency (several months or years) compared with a long-term average (Esfahanian et al. 2017). Drought typically originates from precipitation deficits, also known as meteorological drought. The non-linear cascade of a sustained meteorological drought leads to a reduction in soil moisture and runoff, causing agricultural and hydrological drought, respectively (Liu et al. 2023). The results of these types of droughts eventually affect human societies, creating socio-economic droughts (Felsche and Ludwig 2021). As mentioned above, the propagation of meteorological droughts in the hydrological cycle to other types of droughts is known as temporal propagation. Recently, the spatial propagation of drought at the regional scale has also attracted sufficient attention. Drought propagation across different geographical regions exhibits significant seasonality and spatiotemporal heterogeneity. Large-scale climate patterns, meteorological factors, and human activities play important roles in influencing the drought propagation process (Pachore et al. 2022). Through the interaction of atmospheric circulation and hydrological cycles, drought can extend from one region to adjacent areas, resulting in a cascading effect (Zhang et al. 2022). Currently, many scholars quantify the spatial propagation of drought by analyzing the synchronicity and time delay of drought events across different locations (Liu et al. 2024). Therefore, considering the spatial and temporal propagation traits of droughts is important to enhance a drought early warning system capable of forecasting forthcoming events.

With changes in the spatial and temporal patterns of precipitation and extreme temperatures, droughts at both global and regional scales have shown increasing trends in recent years. Compared with other natural disasters, drought develops slowly and lasts for a long time. Thus, the onset and end of drought are difficult to determine. Its impact is not limited to agriculture but also affects the food supply, the ecological environment, and many other aspects (Kikon and Deka 2021; Cotti et al. 2022). Owing to the dominance of the typical East Asian monsoon climate, droughts are frequent and cause severe losses. Over the past 20 years, the area affected by drought in China has accounted for more than 9.0% of the country’s cultivated area and over 50% of the occurrence of natural disasters in the country (Wang et al. 2021). Therefore, monitoring meteorological drought is an effective early warning for other types of drought and an effective way to reduce the losses caused by droughts (Gholizadeh et al. 2022; Jang et al. 2022).

The outcomes of drought can be difficult to assess because of the complexity of its effects (Gholizadeh et al. 2022; Fard et al. 2022). Over the past few decades, many drought indices have been developed to evaluate and monitor drought events (World 2016). Among the most popular indices are the standardized precipitation index (SPI) (Pande et al. 2022), the Palmer drought severity index (PDSI) (Ma et al. 2018), the standardized precipitation evapotranspiration index (SPEI) (Gaurihar et al. 2023), and the China Z index (CZI) (Chang et al. 2015). The SPEI has the advantage of simultaneously considering both precipitation (P) and potential evapotranspiration (PET) and can comprehensively reflect changes in the surface water balance (Omondi and Lin 2023).

Drought prediction is usually conducted via physical, data-driven, and hybrid models (Vo et al. 2023). Physical models, which rely on the physical principles of atmospheric, hydrological, and ecological systems, have a long history in the field of drought prediction (Huang et al. 2023). These models require extensive observational data and high-performance computing resources for their operation, making them generally suitable only for small watersheds. Data-driven methods have made significant advancements in improving prediction accuracy (Crocetti et al. 2020; Liu and Wang 2021). In particular, the integration of machine learning models has revolutionized drought modeling by enabling computers to discern complex relationships between meteorological and environmental variables (Slater et al. 2023; Latifoglu et al. 2024). With the advancement of deep learning technologies, particularly the emergence of convolutional neural networks (CNNs) (Chaudhari et al. 2021) and recurrent neural networks (RNNs) (Tang et al. 2023), deep learning-based methods for predicting drought via time series data-driven models are becoming increasingly flexible (Oprea et al. 2022; Chen et al. 2024). However, RNN models have long-term dependency and vanishing gradient problems, which are well resolved by the derived bidirectional recurrent neural networks (Bi-RNNs) (Karbasi et al. 2023), long short-term memory (LSTM) (Dikshit et al. 2021), gated recurrent units (GRUs) (Sankalp e tal. 2023), and transformers (Katharopoulos et al. 2020).Owing to their unique advantages in terms of gate control and time dependency, these models have been widely applied in the fields of meteorology and environmental science (Tang et al. 2023). Additionally, deep learning models have demonstrated strong performance in accurately predicting climate parameters and drought indices. Generative adversarial networks (GANs) have been applied in early drought warning systems, utilizing real-time generated meteorological data and radar echo data to monitor signs of drought (Hayatbini 2020; Chen et al. 2022; Moharram and Sundaram 2023). Deep belief networks (DBNs) predict future drought conditions by learning the mapping relationship between input features and drought status (Agana and Homaifar 2018; Huang et al. 2022). Graph neural network (GNN) models improve drought prediction by modeling geographical information as a graph structure, thereby better capturing the spatial propagation of drought (Qiu et al. 2022; Yu et al. 2023). Variants such as the graph convolutional network (GCN) (Bhatti et al. 2023), the graph attention network (GAT) (Chen et al. 2023), and GraphSAGE (Liu et al. 2023) also demonstrate strong performance in constructing spatial information. To enhance the performance of these models, the attention mechanism was introduced (Li et al. 2019, 2020). It is a technique that enables a neural network to selectively attend to the most significant portions of the input and output data, thereby effectively capturing relationships across different aspects and improving the model’s ability to abstract and generalize from the input information (Ehteram and Ghanbari-Adivi 2023). With an improved understanding of the advantages of artificial intelligence, as well as advancements in computational resources and methodologies, hybrid prediction approaches are gaining increasing attention (Slater et al. 2023). Hybrid models integrate the strengths of different methods and have significant potential for enhancing drought prediction (Khan and Maity 2020; Liu and Wang 2021).

Fig. 1
figure 1

Location of study area, all 56 national meteorological stations in Liaoning province

Full size image

Meteorological monitoring stations exhibit complex spatiotemporal dependencies, making it challenging to extract their spatiotemporal features effectively (Stephan et al. 2023). Many researchers have made significant progress in the study of meteorological drought prediction (Araneda et al. 2021; Mercado 2022). Early research focused primarily on the temporal evolution at individual stations, using traditional methods or long short-term memory (LSTM) networks to model the temporal trends of linear or nonlinear relationships between sequences (Dikshit et al. 2021). However, these methods have limited prediction accuracy because of the lack of consideration of interactions between stations. As research has advanced, drought prediction has been viewed as a spatiotemporal sequence problem, tracking droughts through space and time simultaneously and spatial information from the data for predicting varying degrees of drought within a region (Muthuvel and Sivakumar 2024). Therefore, this study proposes a multivariate feature aggregation-based spatiotemporal prediction method for meteorological drought (STAT-LSTM), which contributes to improving drought prediction. The rest of the article is organized as follows. In Section“Materials and methods", an overview of the study area, data collection, spatiotemporal correlations, network architecture, and evaluation metrics are presented. Section“Results" presents the parameter settings and experimental results. In Section“Discussion", some discussion material is presented. Finally, the main conclusions regarding this evaluation framework are presented in Section“Conclusions".

Materials and methods

Study area

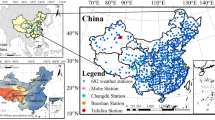
As shown in Fig. 1, Liaoning Province is located in the eastern region of China, covering the latitude of \( 38^\circ 43' - 43^\circ 26' \, \text {N} \) and the longitude of \( 118^\circ 53' - 125^\circ 38' \, \text {E} \). It is bordered by the Yellow Sea and the Bohai Sea to the east, the Inner Mongolia Autonomous Region to the north, Jilin Province to the west, and the Korean Peninsula and South Korea to the south. The topography of Liaoning Province slopes roughly from northwest to southeast, with mountains in the west and plains in the southeast. The region experiences a temperate continental monsoon climate. The eastern coastal areas are moderated by the ocean, resulting in a mild and humid climate, whereas the western inland areas experience a dry climate with low precipitation, making them susceptible to drought. Additionally, the significant interannual variability in typhoons further exacerbates the risk of meteorological droughts.Over the past 57 years, there has been considerable spatial variation in the annual average temperature and precipitation in the study area, with annual average temperatures ranging from 7°C to 10°C and annual precipitation varying between \( 500 \, \text {mm} \) and \( 1100 \, \text {mm} \), decreasing progressively from east to west.

Data

The dataset used in this study was obtained from the China Meteorological Science Data Sharing Service (https://www.data.cma.cn/). To ensure the completeness and continuity of the meteorological datasets, stations with incomplete datasets were excluded, and 56 national meteorological stations in Liaoning Province from 1965 to 2022 were ultimately selected. The meteorological variables used consisted of latitude, altitude (m), average precipitation (mm), monthly average temperature (°C), minimum temperature (°C), maximum temperature (°C), etc. The missing values for each station were filled via linear interpolation of the adjacent station dataset.

This study selects the standardized precipitation-evapotranspiration index (SPEI) at multiple time scales to reflect changes in drought characteristics. SPEI values can be obtained at various time scales, including the SPEI values at 3, 6, 9, and 12 months, each representing different types of drought (Hou et al. 2021). The SPEI package in Python was used to calculate the SPEI at different time scales. According to the standards for meteorological drought classification, drought levels are divided into five categories: no drought, light drought, moderate drought, severe drought, and extreme drought. The classification is as follows (Table 1):

Table 1 Drought classification
Full size table

Spatial and temporal correlation analysis methods

Feature selection is always performed before the model is trained. In this study, the Pearson correlation coefficient was chosen to measure the degree of linear relationship between meteorological features X and Y in the dataset as follows:

$$\begin{aligned} r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} \end{aligned}$$
(1)

where: \( r \) is the Pearson correlation coefficient; \( x_i \) and \( y_i \) are individual observed values of the features \( X \) and \( Y \); \( \bar{x} \) and \( \bar{y} \) are the mean values of the two features.

Considering that not all positively correlated meteorological features have a significant effect on the prediction of drought indices, different correlation thresholds should be tested to evaluate the performance of the prediction. This helps in extracting meteorological features that have a relatively greater influence on the output as input features.

Owing to the spatiotemporal correlation between monitoring stations, drought conditions in one region are spatially connected to those in other regions (Omondi and Lin 2023). Therefore, it is necessary to conduct a spatiotemporal correlation analysis on datasets from multiple monitoring stations. Stations with spatial correlations can be identified by calculating the consistency in drought levels between the target station and other stations during the same period. The choice of probability threshold also requires experimental testing, comparing the results under different thresholds to select the optimal threshold. This threshold should effectively identify correlated stations and minimize false positives.

Given the similarity in climate conditions within certain proximities, an upper limit on the distance between correlated stations should be established. The Haversine formula is used to calculate the distance between two stations:

$$\begin{aligned} d = 2R \cdot \arcsin \left( \sqrt{\sin ^2\left( \frac{\Delta \phi }{2}\right) + \cos (\phi _1) \cdot \cos (\phi _2) \cdot \sin ^2\left( \frac{\Delta \lambda }{2}\right) }\right) \end{aligned}$$
(2)

where: \( \phi _1 \) is the latitude of the two points (in radians), \( \phi _2 \)is the longitude of the two points (in radians), \( \Delta \phi \) is the difference in latitude between the two points (in radians), \( \Delta \lambda \) is the difference in longitude between the two points (in radians), and \( R \) is the radius of the Earth, with an average value of approximately 6,371 kms.

On the basis of the above criteria, we selected stations that have similar climate conditions and significant consistency in drought levels, which have a relatively high influence on the target station.

Methods

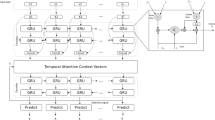
The STAT-LSTM model consists of several components: a feature aggregation module, a self-attention-temporal convolutional network (SA-TCN), a linear encoding layer, a LSTM layer, and a linear output layer. The input dataset is first processed through the convolution module and batch normalization layer to extract preliminary features. These features are then fed into the TCN, which use causal and dilated convolutions to extract temporal sequence features. The self-attention module is added after the convolution layers of the TCN to automatically capture global dependencies in the sequential dataset through a weighted mechanism. A fully connected layer is subsequently used to compress the feature dimensions through encoding. The LSTM layer refines the encoded time series dataset to better capture long-term dependencies. Finally, the hidden states are passed through a linear layer to produce the model’s final output.

Fig. 2
figure 2

SA-TCN structure: adding Self-Attention mechanism after convolutional layer of TCN

Full size image

Feature aggregation module

The spatiotemporal information from monitoring stations that satisfy spatial correlations is integrated, where the input features are represented as a four-dimensional tensor \( X(B, T, N, C) \). Here, \( B \) denotes the number of samples, \( T \) represents the time steps, \( N \) indicates the number of stations, and \( C \) denotes the number of features. Given the input tensor \( X = [X_1, X_2, X_3, \ldots , X_n] \), which is a vector of feature matrices containing spatiotemporal datasets from different stations, the information is integrated across multiple station dimensions. As illustrated in Fig. 4, the convolutional layer aggregates multiple input features via convolutional kernels. These kernels perform a weighted summation of the features and combine these sums into a new feature representation, thus achieving multivariate feature aggregation. Initially, multiple \( 1 \times 1 \) convolutional kernels are employed to expand the dimensionality of the multichannel information. A \( 1 \times 1 \) convolutional kernel is subsequently used to reduce the dimensionality to a single channel, effectively aggregating the dataset features. By increasing the number of dimensions, the model enhances the ability to extract features from information across multiple monitoring stations, thereby consolidating the input dataset into a feature vector \( X_{\text {conv}} \).

$$\begin{aligned} X_{\text {conv}} = \text {ReLU}(\text {BatchNorm}(\text {Conv2D}(X))) \end{aligned}$$
(3)
Fig. 3
figure 3

LSTM structure. \( h_t \) represents the hidden state of the layer, and \( C_t \) represents the cell state

Full size image

SA-TCN

The output of the convolution is passed to the TCN. The TCN consists of two one-dimensional convolutional layers and incorporates causal convolutions, dilated convolutions, and residual connections to ensure that the model can handle long time series information. Each convolutional unit includes a one-dimensional dilated causal convolution, weight normalization, a ReLU activation function, and a dropout operation (Bai et al. 2018). In sequential modeling, causal convolution is expressed as the current moment t being related only to the input at moment t and before moment t. The dilated convolution operation on sequence element s is described as follows:

$$\begin{aligned} F(s) = (x * df)(s) = \sum _{i=0}^{k-1} f(i) \cdot x_{s - d \cdot i} \end{aligned}$$
(4)

where: \( s \) is the input sequence information, \( d \) is the dilation coefficient, \( k \) is the filter size, \( i \) is a nonnegative integer, and \( s - d \cdot i \) is the localization of certain information in the history.

During the training and testing phases of the neural network, different network depths and filter sizes are adjusted and configured to enhance model accuracy, allowing for flexible adaptation to varying scales of temporal feature extraction. The input sequence \( X_{\text {conv}} \) is processed by the TCN to extract local features \( X_{\text {tcn}} \):

$$\begin{aligned} X_{\text {tcn}} = \text {Conv1D}(X_{\text {conv}}) + \text {Activation}(X_{\text {conv}}) \end{aligned}$$
(5)

The TCN captures local temporal dependencies through convolution operations, but its receptive field increases with network depth, which may limit its ability to capture long-range dependencies at shallower layers. To address this issue, as illustrated in Fig. 2, a self-attention mechanism is added after the convolution layers of the TCN to enhance the model’s ability to capture global temporal information. The tensor \( X_{\text {tcn}} \) is transformed into corresponding query vectors \( Q \), key vectors \( K \), and value vectors \( V \). Attention weights are computed on the basis of the similarity between \( Q \) and \( K \), and the attention scores are used to weight and aggregate \( V \) from different inputs to adjust the weights. The self-attention mechanism can be expressed as follows:

$$\begin{aligned} X_{\text {atten}} = \text {Attention}(Q, K, V) = \text {softmax}\left( \frac{Q K^T}{\sqrt{d_k}}\right) V \end{aligned}$$
(6)

where \( Q = X_{\text {tcn}} W_Q \) and where \( W_Q \) is a trainable weight matrix. By employing the self-attention mechanism, each attention head learns different representations, and the outputs of all the attention heads are concatenated to form the final multihead attention output. \( d_k \) represents the dimensionality of each attention head. The model is capable of simultaneously focusing on and integrating different aspects of the input sequence, thereby enhancing its ability to handle long-term dependencies and complex relationships in meteorological datasets. The output of the self-attention mechanism is fused with the original TCN output either through addition or concatenation, resulting in the final feature representation \( X_{\text {fused}} \):

$$\begin{aligned} X_{\text {fused}}= & \text {Conv1D}(X_{\text {conv}}) + \text {Activation}(X_{\text {conv}})\nonumber \\ & + \text {Attention}(Q, K, V) \end{aligned}$$
(7)

LSTM

As illustrated in Fig. 3, the feature sequence obtained from the TCN is passed to the LSTM layer after dimensionality reduction by the encoder for further sequence processing. The LSTM takes the input and the initialized hidden states, outputting the final hidden state \( h_t \) and cell state \( C_t \). The core of the LSTM lies in its ability to selectively remember or forget historical information through gating mechanisms, thereby mitigating the issue of gradient vanishing. The state update equations for LSTM are as follows:

Forget Gate:

$$\begin{aligned} f_t = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f) \end{aligned}$$
(8)

Input Gate:

$$\begin{aligned} i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i) \end{aligned}$$
(9)

Output Gate:

$$\begin{aligned} o_t = \sigma (W_o \cdot [h_{t-1}, x_t] + b_o) \end{aligned}$$
(10)

State Update:

$$\begin{aligned} C_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C}_t \end{aligned}$$
(11)

The output of the LSTM:

$$\begin{aligned} h_t = \text {LSTM}(X_{\text {fused}}) = o_t \cdot \tanh (C_t) \end{aligned}$$
(12)

The output of the LSTM is passed to a fully connected layer, which is used to transform the high-dimensional feature representation into the final prediction result. The fully connected layer is as follows:

$$\begin{aligned} \hat{y} = W \cdot h_t + b \end{aligned}$$
(13)

As illustrated in Fig. 4, the overall architecture of the model is the multivariate feature aggregation-based temporal convolutional network for meteorological drought spatiotemporal prediction (STAT-LSTM). The hyperparameters, loss function, and optimization algorithm are predefined. The hyperparameters include the number of network layers, the size of the convolution kernels, the number of convolution kernels, the learning rate, the dropout rate, the batch size, the sequence length, and the output dimension. The mean squared error (MSE) is selected as the loss function for the training process, and the Adam optimizer is used for gradient descent optimization of the model’s stochastic objective function. During the experimental process, the parameters are adjusted on the basis of the experimental results to optimize the performance and generalizability of the prediction model.

Fig. 4
figure 4

STAT-LSTM architecture diagram, which consists of three components: a feature aggregation module, a self-attentive-temporal convolutional network (SA-TCN), and a long short-term memory network (LSTM)

Full size image

The STAT-LSTM is trained via the integrated multisite information results, and the trained STAT-LSTM is used for drought prediction. First, the training dataset is input into the prediction model, and the vector containing spatiotemporal feature information is fed into STAT-LSTM. The model is trained via the forward propagation method, which effectively learns and extracts abstract representations of the input features by processing them layer by layer. Then, backpropagation is used to update the model parameters. Through continuous iterative optimization, the optimal prediction model is generated.

Model performance evaluation

To more accurately quantify and compare the effectiveness of the models, evaluation metrics are used to measure the model’s performance, e.g., the mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R\(^2\)) (Achite et al. 2022; Elbeltagi et al. 2023). As shown in Eqs. 14-16, where: \( n \) represents the number of samples; \( y_i \) is the variable observation; \( \bar{y} \) is the mean of the variable observation; and \( \hat{y}_i \) is the simulated value of the variable in the statistical model.

$$\begin{aligned} \text {MAE} = \frac{1}{n} \sum _{i=1}^{n} | \hat{y}_i - y_i | \end{aligned}$$
(14)
$$\begin{aligned} \text {RMSE} = \sqrt{\frac{\sum _{i=1}^{n} (y_i - \hat{y}_i)^2}{n}} \end{aligned}$$
(15)
$$\begin{aligned} R^2 = \frac{\sum _{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum _{i=1}^{n} (y_i - \bar{y})^2} \end{aligned}$$
(16)

Results

Experimental settings

In spatiotemporal prediction problems, the size of the sliding window and the prediction step directly affect the prediction results. In most cases, longer prediction steps and sliding windows lead to poorer prediction accuracy.

We normalized the constructed dataset to the range [0, 1] via the Max-Min scaling method to eliminate errors caused by the large differences in magnitude between the data. The dataset was then divided into training and test sets at an 80:20 ratio, with the shape X(B, T, N, C), where B represents the number of samples, T represents the time steps, N represents the number of stations, and C represents the number of features. The number of samples for the training dataset was approximately 560. The steps for predicting the SPEI were determined through multiple experiments, with 3-month, 6-month, 9-month, and 12-month scales set to 4, 5, 8, and 11, respectively. This means that the past 4, 5, 8, and 11 months of the dataset were used to predict the SPEI for the next month at each respective scale.

High-quality model inputs are crucial for improving drought prediction accuracy. Through correlation analysis of meteorological factors and experimental results, precipitation, maximum temperature, average ground temperature, and average water vapor pressure were identified as the four meteorological factors providing the best performance for the input features. After the data were split, the training dataset was fed into the STAT-LSTM model for parameter tuning and model training. To prevent overfitting, a dropout layer with a dropout rate of 0.20 was added to the model. The mean squared error (MSE) was selected as the loss function for the training process, and the Adam optimizer was used to update the weight parameters iteratively, with a learning rate of 0.001. Through extensive testing, we found that the model performs optimally when configured with a 3-layer TCN network and a 3-layer LSTM. Considering the model’s complexity, the size of the training dataset, and the computational resources available, we set the TCN hidden layer sizes to 20, 20, and 32. The LSTM hidden layer size is 20. The prediction model was built via the PyTorch 1.8.0 framework in Python 3.7. The detailed parameters of the final model construction are listed in Table 2.

Table 2 Model parameters
Full size table

Spatial and temporal correlation analysis results

Statistical metrics may not always reflect changes accurately, so spatiotemporal analysis was conducted. The closer the spatial distance \( d \) between stations is, the stronger their relationship. To determine the correlation between meteorological stations, this study uses the Pearson correlation coefficient to calculate the correlation coefficients \( r \) between the time series of nine different meteorological factors for various stations. By testing the prediction performance with different correlation thresholds, the model achieves the best performance when \( d \) is 60 and \( r \) is 0.85. Three out of the 56 stations have an influence on the target station greater than 0.85, and these stations are within 60 km of the target station. We use this threshold as the default value for the model testing below. On the basis of the spatiotemporal correlation analysis, the spatial distribution of the degree of influence of each station toward the target station is shown in Fig. 5. The map shows that the closer the spatial distance between the stations is, the stronger the relationship.

Fig. 5
figure 5

The spatial distribution map of Taian related stations shows that the higher the spatial and temporal correlation between stations, the closer the relationship

Full size image

Ablation experiment

To demonstrate the predictive capability of the STAT-LSTM, we conducted ablation experiments by removing different components: spatiotemporal similarity relationships between stations (TCN-LSTM), feature extraction functions of ATCN (MFSP-LSTM), and long-term dependency capture via LSTM (MFSP-TCN). Table 3, which uses the Taian meteorological station as an example, presents the predictive performance of the STAT-LSTM model and three other models on the test set. These models were tested on predicting SPEI across 3-, 6-, 9-, and 12-month time scales, showing the experimental prediction results and the impacts of different station relationships. Evaluation metrics such as the MAE, RMSE, and \( R^2 \) were used to assess the predictive performance of the models. Models with MAEs and RMSEs close to zero and \( R^2 \) values close to one were considered to have higher accuracy in predicting the SPEI.

Table 3 Comparison of metrics across models at Tai’an station
Full size table
Fig. 6
figure 6

Comparison of model-predicted SPEI-3 values

Full size image
Fig. 7
figure 7

Comparison of model-predicted SPEI-6 values

Full size image

The STAT-LSTM’s advantage lies in its ability to fully consider the interactions between stations and effectively extract spatiotemporal features. To verify the importance of interstation relationships, a TCN-LSTM model was constructed, and it was observed that removing these interstation relationships led to a decline in model performance. This result indicates that incorporating spatiotemporal correlations in a causal network can effectively enhance model performance. Further experiments were conducted by individually removing the TCN module, which has a feature extraction function, and the LSTM module, which captures long-term dependencies. These experiments revealed that the STAT-LSTM outperforms other algorithms in predicting the SPEI at 3-, 6-, 9-, and 12-month intervals, with higher accuracy and stability. For SPEI-3, the model achieved \(\text {MAE} = 0.474\), \(\text {RMSE} = 0.630\), and \(R^2 = 0.613\). For SPEI-6, the metrics were \(\text {MAE} = 0.356\), \(\text {RMSE} = 0.468\), and \(R^2 = 0.748\). For SPEI-9, the results were \(\text {MAE} = 0.284\), \(\text {RMSE} = 0.437\), and \(R^2 = 0.813\). For SPEI-12, the model performed best, with \(\text {MAE} = 0.182\), \(\text {RMSE} = 0.267\), and \(R^2 = 0.934\). The next best models were MFSP-LSTM, TCN-LSTM, and MFSP-TCN. Among these four time-scale SPEI prediction models, SPEI-12 performed the best, indicating that as the time scale increased, the prediction error gradually decreased, and the prediction accuracy improved.

As shown in Figs. 6, 7, 8 and 9, the SPEI predictions and corresponding observations of the ablation experiment models across different time spans. Aside from some relatively large errors caused by a lack of data over certain periods, the drought evaluation results of the SPEI generally align with the actual drought conditions, validating the feasibility of the proposed model in capturing temporal variations.

Fig. 8
figure 8

Comparison of model-predicted SPEI-9 values

Full size image
Fig. 9
figure 9

Comparison of model-predicted SPEI-12 values

Full size image

Comparison experiment

The effectiveness of the model was validated through comparative analysis with the following four methods, highlighting different advantages and performance characteristics:

ARIMA: The ARIMA model predicts the future SPEI via a linear combination of past observations.

Informer: The transformer uses the self-attention mechanism of the transformer to extract features from both long-term and short-term dependencies in time series and performs predictions via an efficient sparse attention mechanism.

TCN-GRU: The TCN-GRU model captures complex dynamic changes in time series while maintaining computational efficiency and is commonly used for time series prediction tasks.

Table 4 Comparison of metrics across models at Tai’an station
Full size table

The comparison results of the different models are shown in Table 4. The proposed STAT-LSTM outperforms all the other three neural network models. The STAT-LSTM model predicted the SPEI-12 with an MAE, RMSE, \( R^2 \), and \( R^2 \) of 0.182, 0.267, and 0.934, respectively. Compared with the ARIMA, GRU, and Informer models, the MFSP-TCN method has strong advantages. The results indicate that our model achieves the highest Pearson correlation coefficient of 0.934, demonstrating strong consistency between the predicted and observed values. The prediction accuracy improves with longer time steps, but the proposed model achieves the best performance in drought index prediction across all time scales compared with the other three models. These results suggest that the proposed model is effective for meteorological drought prediction tasks and has demonstrated strong performance within the study area (Table 3).

Discussion

STAT-LSTM significantly enhances drought prediction performance by effectively integrating spatiotemporal relationships and feature extraction. The model effectively balances accuracy and stability across different time scales, with particularly impressive performance observed at longer time scales. On the basis of the experimental analysis, this study concludes that the model predictive capability is significantly improved, the model demonstrates superior performance, and the model enhances reliability under a variety of conditions, providing strong support for research and applications in related fields.

Compared with the original models, the addition of spatiotemporal relationships enables the STAT-LSTM to achieve superior prediction capabilities and efficiency. By considering both temporal trends and spatial heterogeneity, the STAT-LSTM can more accurately extract key information from complex datasets, thereby improving prediction stability and reliability. In contrast, single models often handle only partial information, leading to instability in predictions.

STAT-LSTM outperforms ARIMA, Informer, and GRU in time series prediction. The ARIMA model relies primarily on linear assumptions for time series datasets, whereas the Informer model, despite its strong ability to model long sequences, may face limitations in handling complex spatiotemporal relationships. The GRU can address some temporal dependencies but is less effective with multiple spatiotemporal interactions. By integrating the ATCN structure, STAT-LSTM not only improves the efficiency of extracting useful features from vast datasets but also enhances the prediction accuracy and robustness through its adaptive weighting mechanism.

STAT-LSTM not only results in smaller prediction errors but also identifies drought events effectively, ensuring high prediction reliability. However, challenges at shorter time scales include data noise, model parameter settings, and associated uncertainties, which may lead to larger prediction deviations. Moreover, rapid changes in meteorological conditions in the short term can make it difficult for the model to capture all dynamic variations, affecting prediction accuracy. Nonetheless, as the time scale increases, these uncertainties are gradually smoothed out and mitigated, leading to reduced prediction errors and significantly improved accuracy. These findings demonstrate that STAT-LSTM exhibits strong stability and accuracy in handling long-term meteorological changes.

Conclusions

Drought is a spatiotemporal environmental risk triggered by precipitation levels falling below the average. The complex topography and local climatic conditions in Liaoning Province significantly increase the difficulty of studying drought mechanisms. Therefore, this study proposes a novel model named the multivariate feature aggregation-based temporal convolutional network for meteorological drought spatiotemporal prediction (STAT-LSTM). The key findings are summarized as follows:

  • Drought at global and regional scales has shown an increasing trend in recent years. Drought propagation across different geographical regions exhibits significant seasonality and spatiotemporal heterogeneity. Large-scale climate patterns, meteorological factors, and human activities play important roles in influencing the drought propagation process. Therefore, the drought prediction problem should be regarded as a spatiotemporal sequence problem, which comprehensively captures the trend of drought in time and the characteristics of its spatial distribution.

  • This study collected meteorological data and calculated its correlations with the SPEI and inter-station correlations. The model achieved optimal performance when d is 60 km or less and r is greater than 0.85. We selected precipitation, maximum temperature, mean ground temperature, and mean vapor pressure as model inputs, which significantly improved drought prediction accuracy.

  • Different time scales of the SPEI reflect varying drought periods and intensities. These drought indices consider meteorological factors and reflect changes in the water balance over different periods. They are commonly used to examine the monthly, seasonal, and interannual variations of meteorological drought. This is crucial for understanding the complexity of droughts, predicting drought trends, and developing effective drought mitigation strategies.

  • The construction of spatiotemporal relationships helps to extract spatial correlations and temporal dependencies. Aside from some relatively large errors caused by missing data over certain periods, the SPEI-based drought assessment results align well with actual drought conditions, verifying the feasibility of the proposed model in capturing temporal variations. Through ablation and comparative experiments, STAT-LSTM showed improved prediction accuracy, which increased as the time scale expanded.

Although this model improves prediction performance compared to other methods, it still has certain limitations. Future research will focus on expanding the model’s prediction time horizon, integrating larger-scale datasets, and incorporating more complex spatial correlation models. Integrating drought prediction with vulnerability mapping could lead to the development of a more comprehensive drought early warning system, enhancing the model’s practical performance. This approach promotes interdisciplinary integration and broader application. It also provides more accurate scientific evidence to support long-term responses to climate change.