Impact of climate change on flood risk with urban resilience perspective using fuzzy logic model

Abstract

Risk is the probability of a hazard and its consequence that can make humans vulnerable and exposed. The flood-related risk assessment and vulnerability of a locality in advance can help to be better prepared for any future hazard situation. Using a fuzzy logic approach, this study examines the climate change-related risk related to floods in Gyor City in Hungary, which floods have historically impacted. The urban resilience aspect was identified using the urban flood resilience model (UFResi-M) to identify flood-related hazards and the relevant coping capacity in the study area. Five hydrometeorological components, i.e., precipitation, river discharge, temperature, snow accumulation, and river level were selected as the most appropriate indicators for the flood caused by climate change. Mann–Kendall test (MKT) and Sen’s slope estimator (SSE) were applied to perform the trend analysis of hydrometeorological components. A fuzzy logic model based on pre-assigned rules was developed to identify climatic change variability and trend prediction in uncertain situations using MATrix LABoratory (MATLAB). The model investigates how hydrometeorological inputs impact the flood situation in the study area. The model was correlated with real-world data showing a significant correlation between precipitation, river discharge, temperature, snow accumulation, and river level. The model values were processed through the resilience index to identify the relation of flood risk with resilience, which shows an inverse relationship between river level and the resilience of the study area.

Introduction

Climate change is a global issue that has received significant attention among researchers and policymakers due to its immense impacts on human activities and the environment (Fawzy et al. 2020; Islam et al. 2022). Climate change is characterized by an increase in extreme weather events, such as heatwaves, floods, droughts, and storms along with global ice sheet retreat and rises in sea level (Salimi and Al-Ghamdi 2020; Vincent 2020), resulting in adverse impacts on water, housing, food security and human communities’ health (Ahima 2020; Goshua et al. 2021) consequently, the future will pose persistent risks to the residents, their properties, and the environment (Hussain et al. 2021). Globally, over the past three decades, there has been a noticeable increase in significant flood disasters, resulting in significant human and economic losses pointing to the impact of climate change (Baig et al. 2022; Rahman et al. 2023).

Urban areas are the main sector impacted by climate change (Abubakar and Dano 2020). Climate extremes have impacted urban areas more than non-urbanized areas as highlighted by several studies (Hu et al. 2023; Roberge and Sushama 2018). This can be understood since global warming and the increased alteration in the local climate of urban localities shows that metropolitan areas are more susceptible to climate change than non-urban areas (Helbing and Meierrieks 2023). The urban climate often enhances the natural variation that initiates due to wide-ranging atmospheric phenomena, which can result in more severe events (Mauree et al. 2019). Several studies demonstrate the impacts of urbanization on the alteration of various climatic phenomena like temperature variation and rainfall patterns. One of the main features of climate change’s impact on urban areas is floods as urbanization influences the alteration in microclimates (Chapman et al. 2017; Sarvari et al. 2019).

The rapid urbanization and increase in extreme rainfall in recent years events due to climate change are fundamental factors in an increase in flooding (Handayani et al. 2020). which has significantly impacted the sustainability of urban development (Ertan and Çelik 2021), as the unsustainable cities will severely be disturbed by the increase in frequency and the flood peak situations (Miguez et al. 2015). Generally, most floods are caused by prolonged heavy rain and the melting of snow and glaciers in certain areas, further intensified by steep slopes, impermeable surfaces, and lack of location-specific flood mitigation measures. The flood risk projection for many cities shows a likelihood of a huge increase in future urban floods in these cities (Januriyadi et al. 2018; Shatkin 2019) with several European cities showing a projection of a twice increase in flood peaks (Hosseinzadehtalaei et al. 2020). Historically, the most prevalent natural hazard in Europe is Floods (Jonkman et al. 2024). The intensity of regional extreme floods in Europe has increased significantly (Berghuijs et al. 2017). This projection of an increase of two to five times peak urban floods compared to current peaks will be a major challenge for urban planners and decision-makers in designing urban flood management (Zevenbergen et al. 2008; Zhou et al. 2019).

The term ‘Resilience’ does not have a general definition but owing to its importance, its use is growing in integrated urban management (Amirzadeh et al. 2022; Coaffee et al. 2018; Meerow et al. 2016; Shamsuddin 2020). In the context of urban areas, resilience is a new pattern of urbanization that impacts our understanding of how to organize and manage urban planning in general and urban hazards in particular (Pour et al. 2020). Its practical implementation can help the stakeholders in decision-making by incorporating the management of disasters and climate risks into urban investments (McDermott 2016; Hussain et al. 2023). The main theme of disaster resilience is the concept of recovering from natural hazard events (Tiernan et al. 2019). Due to global disasters rising frequently and severity, there has been a substantial global focus on disaster resilience. In an urban environment, resilience emphasizes the processes and conditions within communities that enhance or reduce a population’s ability to resist, adapt to, and recover from a shock or perturbation within the shortest possible time and with little or no outside assistance. Resilience, in this way, is synonymous with the notions of “bouncing back” or “jumping back” (Chelleri and Baravikova 2021; Clark 2021). So, it is of great significance for an area to re-evaluate its infrastructure, service provision, and overall vulnerability to climate change, and to improve resilience to such changes and extreme events.

The absence of a standardized procedure for assessing urban risk to climate change has led to various methodologies being used across different cities and regions. Nandalal and Ratnayake (2011) investigated flood risk using a fuzzy approach in the Kalu-Ganga River basin in Sri Lanka with predetermined hazard and vulnerability indicators; however, their study fell short of discussing any meteorological indicators that form an important indicator of the flood. Similarly, a study conducted by Dawood et al. (2021) on a fuzzy logic-based rule model with the selected hydro-meteorological parameters was applied to assist with the variability of climatic change and trend prediction, however, its focus was limited to the output result of the river discharge. In terms of climate change and the flood-related risks associated with it, there has been little effort made to study Gyor City, which has historically been impacted by floods in 1954, 1959, 1963, 1965, 1975, and 1991 and more recently in 2013 in which the flooding occurred due to rise in water level in the Danube River on June 7 due to which 5000 people were impacted in 17 settlements in the study area (Muhoray an Morvai 2015). In their study, Ignjacevic et al. (2020) placed Gyor City in the high-risk category of flood risk while developing a river flood risk map for the economic impacts of climate change. However, no study focused on the risk aspect of climate change for flood situations combined with urban resilience scenarios, which makes this study innovative.

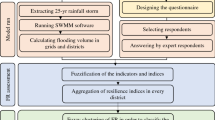
In the study, we analyzed the risk aspect of climate change for flooding in Gyor City. In this context, first, we categorized the parameters for identifying the hazard, exposure, and coping capacity by using the Modified Urban Flood Resilience Model (UFResi-Mm) approach. In the next step, we used four climatic components associated with flooding scenarios in the study area: river discharge, temperature, precipitation, and snow accumulation. The components were processed through the MKT and SSE for statistical analysis to identify the trend and magnitude in all the component data. In the last step, all four components were categorized into monthly low, mean and high, and were processed through fuzzy logic rule-based model to detect climate change in uncertain conditions using MATLAB software. The resultant selected fuzzy set was further analyzed using a normalized resilience index to show the degree of interrelationship between climatic induced risk and resilience.

Study area

Gyor is the capital and largest city of Gyor-Moson-Sopron County and the Western Transdanubia region. The city has a relatively flat topography and has been frequently affected by flooding, the most recent in 2013. Its geographical location is from 17°30′35’’ to 17°47′40’’ east longitude and from 47°44′48’’ to 47°38′7’’ north latitude. For this study, we only selected the inhabited settlement areas of Gyor City, as the city is administratively divided into 18 settlement districts (Fig. 1).

Fig. 1

Location of the study area

The city is located at the junction of four major local rivers i.e., Mosoni-Danube, Raba, Rabca, and Marcal (Fig. 2). Along with these rivers, the Great Danube River flows only 10 km distance from the city center. The amalgamation of all these rivers plays an important role in water fluctuation in the city, hence any disturbance in the water level of these rivers results in a direct impact on the city infrastructure and local community. The city’s hydrological pattern has been undergoing constant changes. During the last two centuries, the city has witnessed an average water level rise of about 3.5 m which now stands at 7.5 m above the underwater surface resulting in flood defenses being constantly raised by the authorities (Molnár 2016).

Fig. 2

Elevation map of the study area

Material and methods

The data about the resilience dimension was obtained from various Government departments. To analyze the risk detection, five hydrometeorological parameters were selected i.e., precipitation, river discharge, temperature snow accumulation, and river level (Fig. 3). The data on climatic anomalies i.e. precipitation and temperature were obtained from the Hungarian Meteorological Service of Met station located in Gyor city while the data about hydrometeorological parameters i.e., river discharge and snow accumulation were obtained from the North Transdanubia Water Directorate of Guage stations located at Gyor city. The river discharge data of four rivers i.e., Raba, Rabca, Danube and Mosoni were collected from the gauge stations present in the study area and was utilized as they are present in the watershed area of Gyor City. Similarly, snow accumulation data was also obtained for two main rivers that are present in the drainage basins of Gyor City, i.e., the Danube and Raba. The spatial maps of the study area were generated using satellite images from ArcGIS software.

Fig. 3

Research process

The MKT and SSE analysis of all four components was carried out using open-source XLSTAT software. The MATLAB toolbox was utilized to analyze the temporal data of climatic components for fuzzy logic and regression models.

Resilience analysis

Risk is a combination of the factors that determine vulnerability and exposure potential for people to a hazard. To identify the reliance factor of flooding in Gyor City, the Modified Urban Flood Resilience Model (UFResi-Mm) approach was utilized and introduced by Tayyab et al. (2021). The UFResi-Mm approach represents the resilience component in decision-making by comparing unique design concepts for flood control alternatives. The UFResi-Mm method is used here as it represents the resilience aspect of floods by incorporating the sensitivity of the system toward floods (hazard and exposure) and its ability to recover from flood-related losses (coping capacity). The UFResi-Mm Equation. One includes elements that can help identify various aspects of flood hazards (IH), exposure (IE), and coping capacity (Ic_c).

The equation represents the UFResi-Mm:

$$\text{UFResi}-\text{Mm}=\lbrack1-(I_{H.}.I_E.I_S)\rbrack.\;m1+\lbrack1-I_{Cc}\rbrack.\;m2$$

(1)

The UFResi-Mm Eq. (1) includes elements that can help in identifying various aspects of flood Hazard (I_H), Exposure (I_E)_, Susceptibility (I_S), and coping capacity (I_Cc) but the susceptibility dimension mainly includes the building infrastructure that is also exposed to floods; therefore, we merged it into Exposure (I_E), susceptibility and exposure. The merging of these two elements is effective as both are positively correlated and so Eq. (1) is consequently modified into the equation:

$$\text{UFResi}-\text{Mm}=\left[1-\left(I_H.I_E\right)\right].\;m1+\left[1-I_{Cc}\right].\;m2$$

(2)

This research concentrated on assessing the sufficiency of the indicators only and evaluating the effect of the weights was not considered a priority. Therefore, the m1 and m2 are constants with an equal value of 0.5. Similarly, in this study, to identify the potential risk of floods to urban resilience three elements of resilience were identified based on the UFResi-Mm approach, i.e.:

• 1. Hazard – the potential damage caused by flooding.

• 2. Exposure – the elements exposed to flooding.

• 3. Coping Capacity – the system’s ability to manage flooding conditions.

Each of the elements comprises pre-selected parameters. The parameters are selected based on the local topographical conditions. Each of the parameters was then further subdivided into sub-parameters. An ArcGIS-based map was then developed for each sub-parameter. The data about the parameters was acquired from different primary and secondary sources mainly through the relative Government departments and literature. So, the hazard, exposure and coping capacity maps were created using ArcGIS software and each parameter was assigned relevant inputs that defined the parameters.

Mann–Kendall Test (MKT)

There are various kinds of statistical methods used in the identification of the trend in time series data, and every method has its strengths and weaknesses (Şen 2014). In this study, the MKT is used to study the trends in the data. The existence of a trend in time series data is not easy to establish, but the monotonic trend can be detected through MKT, one of the most widely accepted statistical tests (Jiqin et al. 2023). The non-parametric rank order of MKT and SSE is often included in statistical analyses to detect trends and ensuing linear or non-parametric regressions to identify historical patterns (Zhang et al. 2009). The MKT is a nonparametric rank-based method used to detect the presence of trends in time series data including meteorological time series data Shepherd et al. 2010; Douglas et al. 2000). The MKT calculates the probability (p-value) with a significance level of 0.05 and is used to test the null hypothesis (H_o). The H_o will be rejected if the p-value is less than or equal to the significance level (α = 0.05), indicating that the time series data has a noteworthy trend (detailed equation in Appendix).

Sen’s Slope Estimator (SSE)

The SSE nonparametric method developed by (Sen 1968) is mainly used in situations where the gap between the data is high (Sam et al. 2022; Moesinger et al. 2020) and when there is a problem in time series change detection then it gives a better result (Rahman and Dawood 2017). The SSE method is used to determine the magnitude of the trend in time series data through trend lines that give the rate of change per period of the recorded time (detailed equation in Appendix).

Fuzzy logic model and membership function using MATLAB

The fuzzy logic approach is one of the most preferable tools for determining multiple truth solutions for uncertain and imprecise situations (Dawood et al. 2021). It works in the same manner as human reasoning based on the inputs that are inserted in the tool (Modarres and Da Silva 2007). The fuzzy logic model was developed by the scientist Lofti Askar Zadeh in 1965 to show expert systems. The model is used in various applications such as automotive systems, environmental control systems, business rules, health care, and complex climatic phenomena. The fuzzy logic model is based on a membership function designed to represent the multi-criteria input variables on a scale between 0 and 1 depending on the ability to be a member of a specific set (Thakkar et al. 2021).

To apply the membership function for Hydrometeorological components, the four components river discharge, temperature, snow and precipitation were processed through a Fuzzy logic model using MATLAB software as inputs while the river level was considered as output as it is the primary source of flood risk impacted by the other four variables. The fuzzy logic model is used to detect trend estimation in those conditions where there is uncertainty in the available data. To create the membership function, 81 rules were generated in MATLAB for the fuzzy system (Fig. 5). The fuzzy logic model works on two well-known Inference systems i.e. Mamdani and Sugeno. In this study, the Mamdani fuzzy inference method (Max–Min method) was applied because compared to Sugeno, it is very helpful for controlling and approximating functions, its output membership function is attendant, and it is well suited to human input (Brahim et al. 2021).

All the components were further divided into monthly ever-highest, monthly ever-lowest, and monthly average. The selected components were divided into five categories of fuzzy logic sets, i.e., low, very low, moderate, high, and very high risk. In the fuzzy logic approach, three significant steps are involved, i.e. inference, fuzzification, and output.

Analysis and interpretation of resilience parameters

Hazard

The hazard susceptibility maps are crucial in coping with flash floods (Cao et al. 2001; Msabi and Makonyo 2021). Similarly, four parameters were selected to identify the hazard: elevation, land use and land cover (lulc), curve number grid (CN grid) and slope. These parameters are crucial in determining hazard evaluation.

The elevation in the study area ranges from 109 to 169 m (Fig. 4a). The LULC was manually classified into 5 major classes based on the topography of the study area (Fig. 4b). These classes are settlement, agriculture, vegetation, barren (land without current use), and water bodies. CN Grid is the capacity of the surface runoff of an area (Xiong et al. 2019). The CN Grid is based on land use and soil type in an area. The analysis of local topography shows that all four Hydrological Soil Groups A and C are dominant in the study area (Fig. 4c). The slope map was developed in ArcGIS and was represented in degrees, which range from 0 to 8.72 degrees, which indicates the relatively flat topography of the study area (Fig. 4d).

Fig. 4

a Elevation, b LULC, c CN Number Grid, d Slope

Exposure

Exposure is the proximity or closeness of a body to potentially hazardous situations (Igulu and Mshiu 2020). The analysis of exposure to an area is vital in predicting possible hazardous events in the future (Criado et al. 2019). The exposure analysis includes four parameters i.e. Proximity to a water body, building structure type and settlement type. The proximity map of the study area was obtained using Sentinel-2 image using the ‘Multiple Ring Buffer’ function of the Proximity tool in ArcGIS software. Four classes were generated in ArcGIS with the assigned values of distance interval from the water bodies of 0–50 m, 50–200 m, 200–500 m, and > 500 m, respectively (Fig. 5a). The proximity zone of 500 m from the inundated areas has the highest priority for shelter locations. It has a higher priority over a 200 m buffer zone. The map was constructed using ArcGIS software with three categories assigned i.e., single-story, double-story, and multi-story buildings (Fig. 5b).

The resultant map shows that most of the area is composed of double (53%) and multi-story structures (45.8%) while single-story structures have a very small proportion (1.2%). Similarly, for the settlement map, the area was classified into residential, commercial, and other types (education, government, religious, and public libraries) using the ArcGIS environment tool (Fig. 5c). The resultant map shows that most of the settlements are composed of residential settlements (59%), followed by commercial (31%) and other settlements (10%).

Fig. 5

a Distance from river b Building type c Function type

Coping capacity

Coping capacity highlights the capability of a system to manage a disaster efficiently (Nachappa et al. 2020; Wang et al. 2020). The coping capacity was analyzed using three parameters i.e. institutional capacity, health facilities, and educational facilities. The institutional capacity for this study was based on the income level, real estate, and various Government amenities. The data were obtained from a Hungarian real estate agency. The data was then processed through ArcGIS software using the ‘Fuzzy Overlay’ tool to visualize the resultant map (Fig. 6a). The data on health facilities locations were obtained from the Gyor city Government website and were processed through ArcGIS software using a GIS environment to generate the resultant map (Fig. 6b). The data for educational facilities was obtained from the Gyor City Government website. The data was processed through a GIS environment to generate the desired resultant map (Fig. 6c).

Fig. 6

a Institutional capacity b Health facilities c Educational facilities

Results and interpretation of MKT and SSE test

MKT and SSE for river level (m)

The maximum river level occurs from the Danube River, followed by Mosoni, Raba, and Rabca (Fig. 7 a, b, c, d). In all the rivers, the river level is maximum in the summer (May–June) and minimum in the winter (Sep-Oct). Monthly-wise, June shows the maximum level from the Danube River while in the case of Mosoni, Raba, and Rabca, March shows the maximum level. Similarly, in October there is a minimum level in Danube, Mosoni, and Rabca rivers while Rabca shows minimum level in August.

Fig. 7

Monthly maximum, minimum, and mean river water level (Linear dashed black line represents a trend in mean). a Danube, b Mosoni, c Rabca, d Raba

The MKT statistical test results show that a statistically significant negative trend in the mean, maximum, and monthly minimum river levels was observed at the Danube and Raba rivers. In contrast, no significant level trend in the mean, maximum, and monthly minimum level Mosoni and Rabca rivers was detected as the p-value in all the rivers is greater than the significance level i.e. 0.05 showing the absence of any statistically significant trend (Table 1). Likewise, the SSE test results show that only the mean and minimum of Rabca and minimum of Mosoni River have a positive. The SSE test results show that among all three rivers, the monthly minimum of Mosoni and Rabca shows the highest magnitude (Q = 0.004), followed by the monthly mean of Raba River (Q = 0.002). The lowest trend magnitude was observed in the monthly minimum of the Danube and Raba rivers, with values of −0.016 each.

Table 1 MKT and SSE results of river level

MKT and SSE for river discharge (m³/s)

The maximum water discharge occurs from the Danube River, followed by Mosoni, Raba, and Rabca (Fig. 8a, b, c, d). In all the rivers, discharge is maximum in the summer (May–June) and minimum in the winter (Sep-Oct). Monthly-wise, June shows the maximum discharge from the Danube River while in the case of Mosoni, Raba, and Rabca, March shows the maximum discharge. Similarly, the minimum discharge data shows that in October, there is a minimum discharge in the Danube, Mosoni, and Rabca rivers, while the minimum discharge for Raba is in August.

Fig. 8

Monthly maximum, minimum, and mean river discharge (Linear dashed black line represents a trend in mean). a Danube, b Mosoni, c Rabca, d Raba

The result of the MKT statistical test shows that there was no significant discharge trend in the mean, maximum, and monthly minimum discharge of any river as the p-value in all the rivers is greater than the significance level i.e. 0.05 showing the absence of any statistical significant trend (Table 2). The results of the SSE test results show that among all the rivers, the monthly mean discharge in the Mosoni River shows the highest magnitude (Q = 0.236) followed by the monthly minimum river discharge at the Danube River (Q = 0.16). In contrast, the monthly maximum discharge in Danube river shows the lowest trend magnitude (Q = −16.85) followed by the mean monthly river discharge in Danube river (Q = −0.178) which shows that the seasonal fluctuation in the Danube is more compared to the other rivers showing that Seasonal discharge patterns of the Danube River have shifted towards increased winter runoff and decreased summer runoff.

Table 2 MKT and SSE results of river discharge

MKT and SSE for monthly temperature (⁰C)

The highest mean monthly temperature was recorded in July, while the lowest was in January. Similarly, the highest maximum monthly temperature was recorded in July, while the lowest was in January. The highest minimum monthly temperature was recorded in July, while the lowest was in January. The highest-ever monthly mean temperature was 12.5⁰C (2019), while the lowest-ever monthly mean temperature was 9 ⁰C in 1980. Similarly, the highest-ever monthly maximum temperature was 20.7 ⁰C (2019), while the lowest-ever monthly maximum temperature was 16.2⁰C in 1996 (Fig. 9). Likewise, the highest-ever monthly minimum temperature was 6.9 ⁰C (2009), while the lowest-ever monthly minimum temperature was 2.6 ⁰C in 1996.

Fig. 9

Monthly maximum, minimum, and mean temperature (Linear dashed black lines represent trend)

The MK statistical test result shows in all three categories, i.e., mean, maximum, and minimum, the p-value is smaller than the significance level, i.e. 0.05; hence there was no significant trend recorded in any of the categories (Table 3), while SSE results show that the positive slope magnitude exists in all three categories with mean monthly temperature shows the highest slope magnitude (Q = 0.054) while minimum monthly temperature shows the lowest slope magnitude (Q = 0.035).

Table 3 MKT and SSE test results of temperature (1973–2022)

MKT and SSE for snow accumulation (kg/m³)

Only the Danube and Raba rivers were selected for analysis as the seasonal snow accumulation occurs only at the basin of these two rivers. The snow accumulation data shows that at the Danube, the highest snow accumulation occurs in March, while the lowest is in May. The highest-ever monthly mean of snow accumulation was 9.76 kg/m³ in 2018 (Fig. 10a). The lowest monthly mean snow accumulation was 2.55 kg/m³ in 2015 (Fig. 10b). Similarly, the highest-ever monthly maximum snow accumulation was 15.05 kg/m³ (2018), while the lowest-ever monthly maximum snow accumulation was 4.32 kg/m³ in 2015. Likewise, the highest-ever monthly minimum snow accumulation was 3.73 kg/m³ (2017), while the lowest-ever monthly minimum snow accumulation was 0.14 kg/m³ in 2022. The snow accumulation data represents the shortest time series among all hydrometeorological components (2013–2022).

Fig. 10

Monthly maximum, minimum, and mean snow accumulation (Linear dashed black line represents a trend in mean). a Danube, b Raba

The resultant analysis of MKT for snow accumulation shows that no prominent trend was detected in either of mean, maximum and minimum monthly snow accumulation in any river as the p-value was less than p = 0.05 in all the categories (Table 4), rejecting H_o, i.e., that there is a trend in accumulation of snow in the available data. Similarly, the SSE test results show that the highest magnitude was observed in the mean monthly snow accumulation at the Danube River (Q = 0.241). In contrast, the lowest magnitude was observed in the minimum monthly snow accumulation at the Danube River (Q = −0.127). In all the other categories of mean, maximum, and minimum snow accumulation, the SSE magnitude was either very low or in some instances, a complete absence of any slope magnitude present.

Table 4 MKT and SSE test results of snow accumulation

MKT and SSE for precipitation (mm)

The data for precipitation was selected based on hourly maximum precipitation events. The analysis shows that the highest concentration of hourly precipitation occurs in May, while the lowest concentration occurs in January and March. The highest-ever monthly mean hourly precipitation was 21.7 mm in 2010, while the lowest monthly mean hourly precipitation was 29.4 mm in 1978 (Fig. 11). Similarly, the highest monthly maximum hourly precipitation was 207.9 mm (2010), while the lowest monthly maximum hourly precipitation was 57.6 mm in 1978. Likewise, the highest monthly minimum hourly precipitation was 21.7 mm (2010), while the lowest monthly minimum hourly precipitation was 0 mm in 2007.

Fig. 11

Monthly maximum, minimum, and mean hourly precipitation. (Linear dashed black lines represent trend)

The MK statistical test for precipitation shows that the P-value in all the categories i.e. monthly mean, maximum, and minimum hourly precipitation is higher than the confidence level (0.05%), showing the absence of any statistically significant trend present in the available data (Table 5). Likewise, SSE results show that the highest magnitude was observed at monthly maximum hourly precipitation (Q = 0.593), while the least slope magnitude was observed at monthly minimum hourly precipitation (Q = −0.055).

Table 5 MKT| and SSE test results of precipitation (1973–2022)

Analysis and interpretation of the fuzzy logic model

Fuzzy input values: MATLAB evaluation rules

Four parameters of hydrometeorological components were considered to contribute significantly to determining the risk factor of a flood. These parameters include precipitation, temperature, water discharge, and snow accumulation. Each of the components was categorized into three portions i.e., monthly lowest, monthly average, and monthly highest (Fig. 12) along with the defining of the membership function (MF) between the range of ‘0’ and ‘1’ for each parameter.

Fig. 12

Fuzzy logic trend detection

The inference rules were established for output evaluation in the proposed fuzzy approximation model using the ‘AND’ connector as a logical operator in designing inference rules. As for the results of MKE and SSE tests, in which all the categories of temperature, i.e., maximum and minimum, show a statistically significant trend in data, the temperature was assigned more weight compared to other components, i.e., if the temperature is the highest while precipitation, water discharge, and snow accumulation are the lowest then the risk will still be average. The ‘AND’ connection is significant in determining the minimum probability of risk prediction with a given predefined set of fuzzy input rules.

The MF for precipitation is calculated as;

$$precipitation\;(mm)=\begin{pmatrix}0.1\;-\;0.33\;=\;Monthly\;Lowest\\0.34\;-\;0.66\;=\;Monthly\;Average\\0.67\;-\;1\;=\;Monthly\;Highest\end{pmatrix}$$

The MF for Temperature is calculated as;

$$Temperature{(^\circ}C)=\begin{pmatrix}0.1\;-\;0.33\;=\;Monthly\;Lowest\\0.34\;-\;0.66\;=\;Monthly\;Average\\0.67\;-\;1\;=\;Monthly\;Highest\end{pmatrix}$$

The MF for River Discharge is calculated as;

$$River\;Discharge\;(m^3/s)=\begin{pmatrix}0.1\;-\;0.33\;=\;Monthly\;Lowest\\0.34\;-\;0.66\;=\;Monthly\;Average\\0.67\;-\;1\;=\;Monthly\;Highest\end{pmatrix}$$

The MF for Snow Accumulation is calculated as;

$$Snow\;Accumulation\;(Km^3)=\begin{pmatrix}0.1\;-\;0.33\;=\;Monthly\;Lowest\\0.34\;-\;0.66\;=\;Monthly\;Average\\0.67\;-\;1\;=\;Monthly\;Highest\end{pmatrix}$$

The output rules were considered river level, i.e.,

The MF for River Level is calculated as.

$$River\;Level\;(m)=\begin{pmatrix}<span class='convertEndash'>1-0.2</span>\;=\;Very\;Low\\0.2\;-\;0.4\;=\;Low\\0.4\;-\;0.6\;=\;Medium\\0.6\;-\;0.8\;=\;High\\0.8\;-\;1\;Very\;High\end{pmatrix}$$

The fuzzy inference engine (fuzzification)

The fuzzy inference system establishes relationships between inputs using an estimated reasoning algorithm, enabling uncertainties to be distributed across the process (Tesfamariam & Saatcioglu 2008). The Fuzzification step includes the creation of rules using fuzzy reasoning. The variables are linked to each other using a predetermined knowledge-based rule system. The fuzzy Inference Engine was created using MKE and SSE results and establishing 81 rules for all the hydroclimatic variables in MATLAB to carry out the fuzzification process. The fuzzy rules include nine output values which were in very low-risk categories i.e. (0.1), followed by 24 values in low categories, i.e. (0.3), medium gets 28 (0.5), high get 15 (0.7) while the very high category (1) of output obtained five values. The output values show that the risk output values fall in the low and medium water level category of 75%. The high and very high-water level category occupied 35% of the output value. The output values of water level were categorized into five components with a predefined criterion range, i.e., very low (VL): (0–20), low (L): (20–40), moderate (M): (40–60), high (H): (60–80), and very high (VH):(80–100) (Fig. 13). Some of the rules developed for risk identification from the fuzzy logic model are the following:

• 1. If the precipitation is the monthly lowest, the temperature is the monthly lowest, and water discharge is the monthly lowest, and snow accumulation is the monthly lowest then the river level is low (0.1) (risk is very low).

• 2. If the precipitation is the monthly highest, temperature is the monthly average, water discharge is the monthly lowest, and snow accumulation is the monthly highest then the river level is low (0.5) (risk is medium).

• 3. If the precipitation is the monthly highest, temperature is the monthly lowest, water discharge is the monthly average, and snow accumulation is the monthly average then the river level is low (0.5) (risk is medium).

• 4. If the precipitation is the monthly highest, temperature is the monthly highest, water discharge is the monthly average, and snow accumulation is the monthly average then the river level is high (0.7) (risk is high).

• 5. If the precipitation is the monthly highest, temperature is the monthly highest, water discharge is the monthly highest, and snow accumulation is the monthly highest then the river level is high (1) (risk is very high).

Fig. 13

Plot of membership functions for each variable

De-fuzzification

The De-fuzzification process is the inverse of fuzzification. The fuzzy output (risk trend) was again converted into physical value in de-fuzzification. The resultant values vary between 0.1 (minimum risk) and 1 (maximum risk). While multiple mathematical techniques exist for defuzzification, the analysis employed the "center of gravity" method, the most widely used method. The resultant defuzzied values of all 81 rules were obtained after the fuzzification process. The resultant output values show that 10 output values were in very low-risk categories, i.e. (0.1), followed by 24 values in all the three output risk categories, i.e., low (0.3), medium 32 (0.5), and high 14 (0.7). Similarly, the very high category (1) of output obtained two values. The output values show that most risk output values fall in the low and medium water level category of 80%. The high and very high-water level category occupied 20% of the output value.

Discussion

The rules that were already generated were merged and then the fuzzy model sets were classified using fuzzy logic resulting in the generation of decision-making outputs. The selection of rules for the membership function is subjective and can be modified according to the situation and context. These memberships are mainly triangular, trapezoidal, Gaussian, Bell, and polynomial types. In this study, the triangular membership function was utilized since the triangular membership function has fewer complexes when splitting values (low, med, and high MF) compared to other membership functions. The membership functions used to fuzzify the hydro-meteorological components are shown in Fig. 13.

The four components and sub-components are put into a fuzzy inference system as input, along with a defined membership function for each input. Fuzzy sets were generated for the dependent (river level) and independent variables (precipitation, river discharge, temperature, and snow accumulation). The dependent (river level) was also treated as a fuzzy variable. In the entire process, the values of all four hydro-meteorological components show fluctuation that changes from low to high level.

After applying the fuzzy logic model to all four hydrometeorological components such as precipitation, temperature, snow accumulation, and river discharge, the de-fuzzification water level value ranged between 0.1 and 0.85, showing the minimum to the maximum river level. The output water level value fluctuates with the input values of hydrometeorological inputs. For instance, three scenarios can be taken as case study:

• 1. Maximum hydrometeorological combination + Extreme weather conditions: In this scenario, the values of river discharge, precipitation, snow accumulation, and temperature are on a very high scale, i.e., 0.96, 0.97, 0.94, 0.95, respectively, then a high-water level (0.85) is obtained showing a very high risk of flooding.

• 2. Moderate hydrometeorological combination + Rare Extreme weather conditions: In this scenario, the values of all four hydrometeorological components are in the medium range, i.e., 0.5, then a very low output of water level of 0.3 is obtained, with a low risk of flooding.

• 3. Low hydrometeorological combination + Clear weather conditions: In this scenario, the values of all four hydrometeorological components are in the medium range, i.e., 0.05. Thus, a very low output of water level 0.1 is obtained, with a very low risk of flooding.

As the fuzzy membership is based on MKT and SSE results, the output of the fuzzy model also fluctuates accordingly, with temperatures more compared to precipitation, river discharge, and snow accumulation along with the low and moderate hydrometeorological combination prevailing with very few scenarios of extreme weather conditions. The study results also contrast to the study by Nandalal and Ratnayake (2011) where parameters of flood area, flood depth, population density and population vulnerability were treated as fuzzy variables to analyze the risk of the climate as the hydro-meteorological aspects of climate are not evaluated. Similarly, the present results analysis corresponds to the study conducted by Dawood et al. (2021), in which a fuzzy process was used to identify the impact of climate change on discharge, but which could be further advanced by incorporating the relevant hydro-metrological components mentioned in this study. The trend analysis results in the study also highlight the temperature and extreme precipitation as a significant factor in hydro-meteorological components that differs from a previous study by Lóczy (2010) who mentioned an increasing flood discharges due to land use in the upper catchments of the Danube River as the only factor contributing to floods.

By applying fuzzy modeling, it is possible to simulate hydro-climatic factors such as temperature, rainfall, snowfall, humidity, sunshine, and discharge to determine the long-term trends, whether positive or negative and to explore the interrelationships among all these parameters. The study’s results can guide the identification of the different scenarios of climatic conditions based on historical trends. Over extended periods, river water levels fluctuate primarily due to variations in hydrologic conditions. A comprehensive flood risk assessment of a flood-prone area is instrumental in guiding decision-makers to make timely and informed decisions. It is beneficial in every phase of a flood-related emergency, including before, during, and after the disaster.

Model validation

To validate the study results, it is essential to confirm them with real-time observations. The regression analysis examines a relationship between two or more variables to determine whether information on one variable can predict or explain data on another. To analyze it, the original data from all the variables (Table 6) were correlated with the membership function in the fuzzy model (Table 7). All the variable’s mean, maximum and minimum data were correlated with the mean, maximum, and minimum fuzzy logic values. The real data of variables were considered independent variables while the fuzzy logic membership values were considered dependent variables. To identify the relation between the actual values and fuzzy logic values, the Pearson product-moment correlation coefficient was applied, which is a type of correlation that assesses the degree of relationship between two variables. Pearson’s r value ranges from −1 to 1, where 0 indicates no correlation, 1 signifies perfect positive correlation, and −1 represents perfect negative correlation. The Pearson Correlation Coefficient formula is as follows.

$$r=\frac{n\left(\sum xy\right)-(\sum x)(\sum y)}{\sqrt{\left[n\sum x^2-\left(\sum x\right)^2\right]\left[n\sum y^2-\left(\sum xy\right)^2\right]}}$$

(3)

where terms in Eq. 3 are,

r:

Pearson Coefficient

n:

number of data points

∑xy:

sum of the product of the x-value and y-value for each point in the data set

∑x:

sum of the x scores

∑y:

sum of the y scores

∑x²:

sum of the squared x scores

∑y²:

sum of the squared y scores

Table 6 Actual values of variables

Table 7 Fuzzy model values of variables

Table 8 shows a very high correlation between all the variables of hydrometeorological data. This proves that the results produced by our fuzzy inference system are practical and align with the data observed in reality. The correlation results also highlight the effectiveness of the rules and their results from the fuzzy logic model.

Table 8 Person coefficient values

Error testing

To analyze the error in the fuzzy model, four metrics of regression analysis were used, i.e., R² (Coefficient of determination), MAPE (Mean absolute percentage Error), MSE (Mean Squared Error), and RMSE (Root Mean Squared Error) with each of these metrics is calculated using Eqs. 4, 5, 6 and 7, respectively. The R² shows how well the selected independent variables explain the variability in the dependent variable, MAPE is the measurement of the mean percentage of error between expected and actual values, MSE is the measurement of the mean squared difference between the calculated and actual values and RMSE is the mean squared difference between the calculated and actual values. The results of all four regression analyses, i.e., R², MAPE, MSE, and RMSE were 0.994, 0.122, 0.22, and 0.004, respectively. The results of all tests show the high accuracy of system model verification.

$$R^2\;=\;1\;-\;\frac{\sum{(y_i\;-\;\overline y)}^2}{\sum\;{(y_i\;-\;\overline y)}^2\;}$$

(4)

$$MAPE=\frac{100}n\sum\nolimits_{i=1}^n\left|\frac{Yi-\widehat Yi}{Yi}\right|$$

(5)

$$MSE=\frac1N\sum\nolimits_{i=1}^N\left(yi-\widehat y\right)^2$$

(6)

$$RMSE=\sqrt{\frac1n\sum\nolimits_{i=1}^n{(Y_i-{\widehat Y}_i)}^2}$$

(7)

Resilience index

The resilience index was introduced to determine if the climate-based fuzzy risk correlates with the resilience factor. In the disaster context, the resilience is treated inversely to vulnerability, thus, increasing resilience would reduce vulnerability and vice versa (Proag 2014) therefore the INFORM (Index for Risk Management) model was utilized that incorporates the three elements of risk as outlined in the United Nations Office for Disaster Risk Reduction (UNDRR) definition (De Groeve et al. 2015). The INFORM risk model balances two significant forces of vulnerability i.e. the hazard and exposure dimension on one side and the lack of capacity dimensions on the other. The aspects of physical vulnerability and exposure are integrated in the hazard and exposure dimension while the lack of coping capacity dimension addresses the inability to cope and recover. In order to accommodate the INFORM Risk methodology, where the vulnerability variable is split among three dimensions, the equation is updated to:

The INFORM equation is represented as:

$$Risk\;=\;Hazard^{1/3}\;\times\;Exposure^{1/3}\;\times\;Lack\;of\;coping\;capacity^{1/3}$$

(8)

The R-value was obtained from the selected fuzzy sets (Table 7). Resilience is calculated in such a way that it is inversely related to the risk a community faces. Therefore, a greater community resilience score leads to a lower Risk Index score. As Eq. 8 represents the resilience aspect, Eq. 8 was modified by introducing the R (risk) as a denominator to determine any correlation of resilience to risk factors. The R as a denominator shows how much resilience values, i.e., hazard, exposure, and coping capacity change with the R-value of fuzzy logic.

$$Resileince\;Index\;=\;\frac{Hazard^{1/3}\;\times\;Exposure^{1/3}\;\times\;Lack\;of\;coping\;capacity^{1/3}}{Risk}$$

(9)

After the calculation, the resultant values of Eq. 9 were normalized using Min–max normalization, a standard statistical method for standardizing data values to a common scale by normalizing the data between 0 and 1. Every data has its minimum value converted to a zero, its maximum value converted to a one, and all other values converted to a decimal between 0 and 1. The normalization of values was carried out to relate it to the selected fuzzy logic set (Table 5). Likewise, the resilience was categorized into three levels based on the normalized value of UFresi-Mm resultant value of fuzzy risk, i.e., 0–2 (very low), 2–4 (low), 4–6 (medium), 6–8 (high), 8–10 (very high).

The normalized value ranges from a minimum of 0 to a maximum of 1. The results show that the risk factor is inversely proportional to the resilience level, i.e., the higher the risk threshold, the lower the resilience level, and vice versa (Table 9).

Table 9 Risk-based resilience index

Limitations of the present study

The present research focused on assessing flood susceptibility in urban areas. The accuracy of the model’s predictions could be significantly affected by the quality of the data provided. Furthermore, the limitations tied to historical data pose an additional challenge. It is possible that the historical disaster data included for model training does not include all incidences, particularly in unusual circumstances with a restricted supply of data. Similarly, the forecasting was based on past data and might not account for newly developed systems, technologies, or processes in the future. As a result, the model might need to be retested using more recent data sets to improve it even further. The overall global trend shows an increasing temperature which coincides with the findings of this paper. However, it fell short in predicting future climate trends for the study area, which needs further analysis and broad data utilization. Similarly, the resilience parameters used here are limited to selected themes based on their importance in the study area and parameters like snow accumulation data have a limited time series. Also, the fuzzy logic limitations include the design of user-defined rules that can vary according to the situation along with broader testing.

Conclusion

In the present study, an attempt was made to identify climate change prediction and its impact on risk assessment in urban areas. The study area has historically been impacted by climatic calamities, particularly floods, therefore there is a need for a suitable approach to analyze the flood risk associated with climate change. To analyze the risk of floods in the urban area, the resilience aspect of the study area was first analyzed using the UFResi-Mm approach. Then, four hydro-meteorological components (precipitation, river discharge, temperature, and snow accumulation) were analyzed and modeled. The four components were first analyzed using the MKT and SSE approach to detect any trend in the data. They were then processed through the fuzzy logic rule-based model to determine the risk associated with the hydro-meteorological components.

Globally, the fuzzy logic approach is widely used for various purposes, with applications in various fields, including climate risk detection. The fuzzy logic-based approach effectively identifies the risk factor with a fair distribution. It is the preferable approach as it does not require standardization of variables because its output membership function value always varies between the scale of 0–1 irrespective of any variation in the inputs considered. The presented approach is very applicable in urban area risk assessment as it grasps the fuzziness of hazard, exposure, and coping capacity of an urban area by taking uncertainty into consideration of hydro-meteorological components, i.e., precipitation, river discharge, temperature, and snow accumulation. Furthermore, the fuzzy logic model provides a better understanding and solution to interpreting, assessing, and learning about risks that are not well understood by identifying the degree of relative falsehood and truth as a number between 0 and 1.

The proposed Fuzzy logic method was applied to forecast the flood risk based on water level with the inputs from the hydrometeorological components that directly impact the water level of river systems. Here, we tested the model using data from only one city. In the future, comparable data sets from other urban centers could be utilized to assess the method’s robustness and average regional bias. A wide range of potential future conditions and their resultant risk level can be investigated by changing the input variables. This capability offers an easy-to-use method for evaluating potential risks under different climate conditions, which enables more informed planning and adaptation strategies in conservation efforts and policy development.

Appendix

Mann–Kendall Test (MKT) Equation

Let × 1, × 2,..…xn represent n data points where xj represents the data point at time j. Then the MKT Sum (S) is statistically derived as follows:

$$S= \sum_{i=1}^{n-1} \sum_{j=i+1}^{n}\mathit{sign}\left({x}_{j}-{x}_{i}\right)$$

If the resultant value of S is a positive large number, then values obtained later tend to be larger than the earlier obtained value with an indication of an upward trend. If the resultant value of S is a negative large number, then the values obtained later tend to be smaller than the earlier obtained value with an indication of a downward trend. If the resultant value of S is a small number, then there is no indication of any trend.

n = Length of the data number

x = Value of data number

i and j = Time series

sign $(x_j\;-\;x_i)$ = + 1, 0, or -1

sign $(x_j\;-\;x_i)$ = 1 if $x_{j-}\;x_i\;>\;0$ 

 = if $x_{j-}\;x_k\;=\;0$ 

 = -1 if $x_{j\;-\;}x_k\;<\;0$ 

The variance can be calculated statistically through the following formula:

$$var= \frac{n\left(n-1\right)\left(2n+5\right)- {\sum }_{i=0}^{m}{x}_{i}-1)(2{x}_{i}+5)}{18}$$

Sen’s Slope Estimator (SSE) Equation

The slope for all relative samples can be calculated as,

$$f\left(t\right)= Qt + B$$

where Q represents Slope, B represents constant, and t represents time.

To obtains the slope estimate (Q), first, the slope of all data numbers (value) of all the time series is calculated using the equation:

$${Q}_{i}= \frac{{X}_{i - }{X}_{j}}{j-k}$$

where X_i represents and X_j represents the data pair values at time j and k (j > k), respectively.

$$i=\;1,\;2,\;n$$

If there is a presence of only datum in each period, then N = n(n-1)/2, where n = number of periods. Similarly, if each period contains more than one datum then N < n(n − 1)/2. The slope in SSE is the median of these N values of ${Q}_{i}$.

${Q}_{med}={Q}_{\left[\frac{\left(N+1\right)}{2}\right]}$, If N is odd.

Or.

${Q}_{med}= \frac{{Q}_{\left[N/2\right]} +{ Q}_{\left[\left(N+2\right)/2\right]} }{2}$, If N is even.

To obtain the trend and magnitude of the slope, the value of Q_med is calculated with the help of a non-parametric model. The positive value of Q_i indicates an increasing trend, while the negative value of Q_i indicates a decreasing trend, and the zero value indicates no trend in time series analysis.