Skip to main content
Springer Nature Link
Log in

Modelling and stability of a synthetic drugs transmission model with relapse and treatment

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

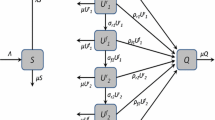
In this paper, a synthetic drugs transmission model with treatment is formulated based on the principles of mathematical epidemiology. The model considers that relapse can occur among those individuals who have a history of drug abuse and we distinguish the addiction rates of susceptible individuals who have a history of drug abuse and those who have not. The global dynamics of this model are determined by the basic reproduction number, \(R_{0}\), under certain conditions. If \(R_{0}<1\), the drug-free equilibrium is globally exponentially stable for a special case and the exponential convergence rate can be unveiled, and if \(R_{0}>1\), the drug-addiction equilibrium is globally asymptotically stable under certain conditions. Sensitivity analysis is performed to seek for effective control measures for drug abuse. Numerical simulations are also carried out to confirm the analytical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Castellani, B., Wedgeworth, R., Wootton, E., Rugle, L.: A bi-directional theory of addiction: examining coping and the factors related to substance relapse. Addict. Behav. 22(1), 139 (1997)

    Article  Google Scholar 

  2. Cui, J.A., Tao, X., Zhu, H.: An SIS infection model incorporating media coverage. Rocky Mt. J. Math. 38(2008), 1323–1334 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  3. Fang, B., Li, X., Martcheva, M., Cai, L.: Global stability for a heroin model with two distributed delays. Discrete Contin. Dyn. B 19(3), 715–733 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  4. Grunbaum, J.A., Tortolero, S., Weller, N., Gingiss, P.: Cultural, social, and intrapersonal factors associated with substance use among alternative high school students. Addict. Behav. 25, 145–151 (2000)

    Article  Google Scholar 

  5. Heffernan, K., Cloitre, M., Tardiff, K., Marzuk, P.M., Portera, L., Leon, A.C.: Childhood trauma as a correlate of lifetime opiate use in psychiatric patients. Addict. Behav. 25(5), 797 (2000)

    Article  Google Scholar 

  6. Huang, G., Liu, A.: A note on global stability for a heroin epidemic model with distributed delay. Appl. Math. Lett. 26(7), 687–691 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  7. Huo, H., Dang, S., Li, Y.: Stability of a two-strain tuberculosis model with general contact rate. Abstr. Appl. Anal. 2010(6), 759–786 (2010)

    MathSciNet  MATH  Google Scholar 

  8. Huo, H., Zhu, C.: Influence of relapse in a giving up smoking model. Abstr. Appl. Anal. 2013, 123–185 (2013)

    MathSciNet  MATH  Google Scholar 

  9. Kalula, A.S., Nyabadza, F.: A theoretical model for substance abuse in the presence of treatment. S. Afr. J. Sci. 108(3/4), 96–107 (2012)

    Google Scholar 

  10. Katerndahl, D.A., Realini, J.P.: Relationship between substance abuse and panic attacks. Addict. Behav. 24(5), 731–736 (1999)

    Article  Google Scholar 

  11. LaSalle, J.P.: The stability of dynamical systems. Soc. Ind. Appl. Math. 27(11), 1121–1130 (1976)

    Google Scholar 

  12. López-Torrecillas, F., Godoy García, J.F., Pérez, G.M., Godoy, I.D., Sánchez-Barrera, M.B.: Variables modulating stress and coping that discriminate drug consumers from low or nondrug consumers. Addict. Behav. 25(1), 161–165 (2000)

    Article  Google Scholar 

  13. Ma, M., Liu, S., Li, J.: Does media coverage influence the spread of drug addiction? Commun. Nonlinear Sci. 50, 169–179 (2017)

    Article  MathSciNet  Google Scholar 

  14. Mulone, G., Straughan, B.: A note on heroin epidemics. Math. Biosci. 218(2), 138 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  15. Mushanyu, J., Nyabadza, F., Stewart, A.G.R.: Modelling the trends of inpatient and outpatient rehabilitation for methamphetamine in the Western Cape province of South Africa. BMC Res. Notes 8(1), 1–13 (2015)

    Article  Google Scholar 

  16. Nyabadza, F., Hovemusekwa, S.D.: From heroin epidemics to methamphetamine epidemics: modelling substance abuse in a South African province. Math. Biosci. 225(2), 132–140 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  17. Nyabadza, F., Njagarah, J.B.H., Smith, R.J.: Modelling the dynamics of crystal meth (Tik) abuse in the presence of drug-supply chains in South Africa. Bull. Math. Biol. 75(1), 24–48 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Obot, I.S., Anthony, J.C.: Association of school dropout with recent and past injecting drug use among African American adults. Addict. Behav. 24(5), 701 (1999)

    Article  Google Scholar 

  19. Sahu, G.P., Dhar, J.: Dynamics of an SEQIHRS epidemic model with media coverage, quarantine and isolation in a community with pre-existing immunity. J. Math. Anal. Appl. 421(2), 1651–1672 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. Samanta, G.P.: Dynamic behaviour for a nonautonomous heroin epidemic model with time delay. J. Comput. Appl. Math. 35(1–2), 161–178 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Sun, C., Yang, W., Arino, J., Khan, K.: Effect of media-induced social distancing on disease transmission in a two patch setting. Math. Biosci. 230(2), 87–95 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  22. Tchuenche, J.M., Dube, N., Bhunu, C.P., Smith, R.J., Bauch, C.T.: The impact of media coverage on the transmission dynamics of human influenza. BMC Public Health 11(Suppl 1), S5 (2011)

    Google Scholar 

  23. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  24. Wang, X., Yang, J., Li, X.: Dynamics of a heroin epidemic model with very population. Appl. Math. 2(6), 732–738 (2011)

    Article  MathSciNet  Google Scholar 

  25. White, E., Comiskey, C.: Heroin epidemics, treatment and ODE modelling. Math. Biosci. 208(1), 312 (2007)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work is partially supported by the National Natural Science Foundation of China (No. 11601405).

Author information

Authors and Affiliations

  1. College of Science, Northwest A&F University, Yangling, 712100, Shaanxi, China

    Pengyan Liu, Liang Zhang & Yifan Xing

Authors
  1. Pengyan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Liang Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yifan Xing
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Liang Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, P., Zhang, L. & Xing, Y. Modelling and stability of a synthetic drugs transmission model with relapse and treatment. J. Appl. Math. Comput. 60, 465–484 (2019). https://doi.org/10.1007/s12190-018-01223-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-018-01223-0

Keywords

Mathematics Subject Classification