Skip to main content

Advertisement

Springer Nature Link
Log in

Neural network based on systematically generated smoothing functions for absolute value equation

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

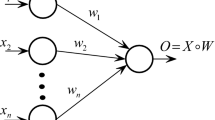
Abstract

In this paper, we summarize several systematic ways of constructing smoothing functions and illustrate eight smoothing functions accordingly. Then, based on these systematically generated smoothing functions, a unified neural network model is proposed for solving absolute value equation. The issues regarding the equilibrium point, the trajectory, and the stability properties of the neural network are addressed. Moreover, numerical experiments with comparison are presented, which suggests what kind of smoothing functions work well along with the neural network approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Bouzerdoum, A., Pattison, T.R.: Neural network for quadratic optimization with bound constraints. IEEE Trans. Neural Netw. 4, 293–304 (1993)

    Article  Google Scholar 

  2. Beck, A., Teboulle, M.: Smoothing and first order methods: a unified framework. SIAM J. Optim. 22, 557–580 (2012)

    Article  MathSciNet  Google Scholar 

  3. Bauschke, H., Combettes, P.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2016)

    MATH  Google Scholar 

  4. Chen, C., Mangasarian, O.L.: A class of smoothing functions for nonlinear and mixed complementarity problems. Comput. Optim. Appl. 5, 97–138 (1996)

    Article  MathSciNet  Google Scholar 

  5. Cichochi, A., Unbenhauen, R.: Neural Network for Optimization and Signal Processing. Wiley, New York (1993)

    Google Scholar 

  6. Hopfield, J.J., Tank, D.W.: Neural computation of decision in optimization problems. Biol. Cybern. 52, 141–152 (1985)

    MATH  Google Scholar 

  7. Hu, S.-L., Huang, Z.-H.: A note on absolute value equations. Optim. Lett. 4, 417–424 (2010)

    Article  MathSciNet  Google Scholar 

  8. Hu, S.-L., Huang, Z.-H., Zhang, Q.: A generalized Newton method for absolute value equations associated with second order cones. J. Comput. Appl. Math. 235, 1490–1501 (2011)

    Article  MathSciNet  Google Scholar 

  9. Jiang, X., Zhang, Y.: A smoothing-type algorithm for absolute value equations. J. Ind. Manag. Optim. 9, 789–798 (2013)

    Article  MathSciNet  Google Scholar 

  10. Ketabchi, S., Moosaei, H.: Minimum norm solution to the absolute value equation in the convex case. J. Optim. Theory Appl. 154, 1080–1087 (2012)

    Article  MathSciNet  Google Scholar 

  11. Kreimer, J., Rubinstein, R.Y.: Nondifferentiable optimization via smooth approximation: general analytical approach. Ann. Oper. Res. 39, 97–119 (1992)

    Article  MathSciNet  Google Scholar 

  12. Liao, L.-Z., Qi, H.-D.: A neural network for the linear complementarity problem. Math. Comput. Model. 29, 9–18 (1999)

    MathSciNet  MATH  Google Scholar 

  13. Liao, L., Qi, H.-D., Qi, L.: Solving nonlinear complementarity problem with neural networks: a reformulation method approach. J. Comput. Appl. Math. 131, 343–359 (2001)

    Article  MathSciNet  Google Scholar 

  14. Mangasarian, O.L.: Absolute value programming. Comput. Optim. Appl. 36, 43–53 (2007)

    Article  MathSciNet  Google Scholar 

  15. Mangasarian, O.L.: Absolute value equation solution via concave minimization. Optim. Lett. 1, 3–5 (2007)

    Article  MathSciNet  Google Scholar 

  16. Mangasarian, O.L.: A generalized Newton method for absolute value equations. Optim. Lett. 3, 101–108 (2009)

    Article  MathSciNet  Google Scholar 

  17. Mangasarian, O.L.: Primal–dual bilinear programming solution of the absolute value equation. Optim. Lett. 6, 1527–1533 (2012)

    Article  MathSciNet  Google Scholar 

  18. Mangasarian, O.L.: Absolute value equation solution via dual complementarity. Optim. Lett. 7, 625–630 (2013)

    Article  MathSciNet  Google Scholar 

  19. Miao, X.-H., Hsu, W.-M., Chen, J.-S.: The solvabilities of three optimization problems associated with second-order cone (submitted manuscript) (2018)

  20. Miao, X.-H., Yang, J.-T., Saheya, B., Chen, J.-S.: A smoothing Newton method for absolute value equation associated with second-order cone. Appl. Numer. Math. 120(October), 82–96 (2017)

    Article  MathSciNet  Google Scholar 

  21. Mangasarian, O.L., Meyer, R.R.: Absolute value equation. Linear Algebra Appl. 419, 359–367 (2006)

    Article  MathSciNet  Google Scholar 

  22. Moreau, J.J.: Proximité et dualité dans un espace Hilbertien. Bulletin de la Société Mathématique de France 93, 273–299 (1965)

    Article  MathSciNet  Google Scholar 

  23. Nesterov, Y.: Smooth minimization of non-smooth functions. Math. Program. 103, 127–152 (2005)

    Article  MathSciNet  Google Scholar 

  24. Nguyen, C.T., Saheya, B., Chang, Y.-L., Chen, J.-S.: Unified smoothing functions for absolute value equation associated with second-order cone. Appl. Numer. Math. 135, 206–227 (2019)

    Article  MathSciNet  Google Scholar 

  25. Prokopyev, O.A.: On equivalent reformulations for absolute value equations. Comput. Optim. Appl. 44, 363–372 (2009)

    Article  MathSciNet  Google Scholar 

  26. Qi, L.: Convergence analysis of some algorithms for solving nonsmooth equations. Math. Oper. Res. 18, 227–244 (1993)

    Article  MathSciNet  Google Scholar 

  27. Qi, L., Sun, D., Zhou, G.-L.: A new look at smoothing Newton methods for nonlinear complementarity problems and box constrained variational inequality problems. Math. Program. 87, 1–35 (2000)

    Article  MathSciNet  Google Scholar 

  28. Qi, L., Sun, D.: Smoothing functions and smoothing Newton method for complementarity and variational inequality problems. J. Optim. Theory Appl. 113, 121–147 (2002)

    Article  MathSciNet  Google Scholar 

  29. Rohn, J.: A theorem of the alternatives for the equation \(Ax+B|x|=b\). Linear Multilinear Algebra 52, 421–426 (2004)

    Article  MathSciNet  Google Scholar 

  30. Rohn, J.: Solvability of systems of interval linear equations and inequalities. In: Fiedler, M., Nedoma, J., Ramik, J., Rohn, J., Zimmermann, K. (eds.) Linear Optimization Problems with Inexact Data, pp. 35–77. Springer, Berlin (2006)

    Chapter  Google Scholar 

  31. Rohn, J.: An algorithm for solving the absolute value equation. Electron. J. Linear Algebra 18, 589–599 (2009)

    MathSciNet  MATH  Google Scholar 

  32. Saheya, B., Yu, C.-H., Chen, J.-S.: Numerical comparisons based on four smoothing functions for absolute value equation. J. Appl. Math. Comput. 56, 131–149 (2018)

    Article  MathSciNet  Google Scholar 

  33. Sun, J.-H., Chen, J.-S., Ko, C.-H.: Neural networks for solving second-order cone constrained variational inequality problem. Comput. Optim. Appl. 51, 623–648 (2012)

    Article  MathSciNet  Google Scholar 

  34. Tank, D.W., Hopfield, J.J.: Simple neural optimization networks: an A/D converter, signal decision circuit, and a linear programming circuit. IEEE Trans. Circuits Syst. 33, 533–541 (1986)

    Article  Google Scholar 

  35. Voronin, S., Ozkaya, G., Yoshida, D.: Convolution based smooth approximations to the absolute value function with application to non-smooth regularization. arXiv:1408.6795v2 [math.NA]

  36. Wang, F., Yu, Z., Gao, C.: A smoothing neural network algorithm for absolute value equations. Engineering 7, 567–576 (2015)

    Article  Google Scholar 

  37. Yong, L.Q., Liu, S.Y., Tuo, S.H.: Transformation of the linear complementarity problem and the absolute value equation. J. Jilin Univ. (Sci. Ed.) 4, 638–686 (2014)

    Google Scholar 

  38. Yamanaka, S., Fukushima, M.: A branch and bound method for the absolute value programs. Optimization 63, 305–319 (2014)

    Article  MathSciNet  Google Scholar 

  39. Zak, S.H., Upatising, V., Hui, S.: Solving linear programming problems with neural networks: a comparative study. IEEE Trans. Neural Netw. 6, 94–104 (1995)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mathematical Science, Inner Mongolia Normal University, Hohhot, 010022, Inner Mongolia, People’s Republic of China

    B. Saheya

  2. Department of Mathematics, National Taiwan Normal University, Taipei, 11677, Taiwan

    Chieu Thanh Nguyen & Jein-Shan Chen

Authors
  1. B. Saheya
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chieu Thanh Nguyen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jein-Shan Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jein-Shan Chen.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

B. Saheya: The author’s work is supported by National Key R&D Program of China (Award No.: 2017YFC1405605) and Foundation of Inner Mongolia Normal University (Award No.: 2017YJRC003)

J.-S. Chen: The author’s work is supported by Ministry of Science and Technology, Taiwan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saheya, B., Nguyen, C.T. & Chen, JS. Neural network based on systematically generated smoothing functions for absolute value equation. J. Appl. Math. Comput. 61, 533–558 (2019). https://doi.org/10.1007/s12190-019-01262-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-019-01262-1

Keywords

Mathematics Subject Classifications