Abstract
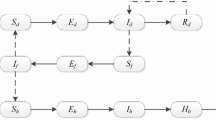
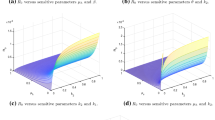
In this paper, we discuss some of the dynamical characteristics of a visceral leishmaniasis (VL) model with time delay. We have derived sufficient conditions to ensure the stability of the considered delayed VL model at the steady states. Taking the time delay as a bifurcation parameter, we have established a criteria for the existence of Hopf bifurcation of the considered model. Moreover, conditions for global stability of the steady states are also presented. Finally, some numerical simulations are given to show the effectiveness of our theoretical results.






Similar content being viewed by others
References
Hethcote, H.W.: The mathematics of infectious diseases. SIAM Rev. 42(4), 599–653 (2000)
Anderson, R.M., May, R.M.: Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford (1992)
Hethcote, H.W.: Qualitative analyses of communicable disease models. Math. Biosci. 28(3–4), 335–356 (1976)
Hu, Z., Ma, W., Ruan, S.: Analysis of sir epidemic models with nonlinear incidence rate and treatment. Math. Biosci. 238(1), 12–20 (2012)
Tian, J.P., Wang, J.: Global stability for cholera epidemic models. Math. Biosci. 232(1), 31–41 (2011)
Liu, X., Yang, L.: Stability analysis of an seiqv epidemic model with saturated incidence rate. Nonlinear Anal. Real World Appl. 13(6), 2671–679 (2012)
Chitnis, N., Cushing, J.M., Hyman, J.: Bifurcation analysis of a mathematical model for malaria transmission. SIAM J. Appl. Math. 67(1), 24–45 (2006)
Lv, C., Huang, L., Yuan, Z.: Global stability for an HIV-1 infection model with beddington-deangelis incidence rate and ctl immune response. Commun. Nonlinear Sci. Numer. Simul. 19(1), 121–127 (2014)
Ponte-Sucre, A.: Introduction: leishmaniasis—the biology of a parasite. In: Ponte-Sucre, A., Diaz, E., Padrón-Nieves, M. (eds.) Drug Resistance in Leishmania Parasites, pp. 1–12. Springer, Vienna (2013)
Oryan, A., Akbari, M.: Worldwide risk factors in leishmaniasis. Asian Pac. J. Trop. Med. 9(10), 925–932 (2016)
CDC division of parasitic diseases, leishmaniasis. http://www.dpd.cdc.gov/dpdx/HTML/Leishmaniasis.htm. Accessed 21 Jan 2019
Desjeux, P.: Leishmaniasis: current situation and new perspectives. Comp. Immunol. Microbiol. Infect. Dis. 27(5), 305–318 (2004)
Chappuis, F., Sundar, S., Hailu, A., Ghalib, H., Rijal, S., Peeling, R.W., Alvar, J., Boelaert, M.: Visceral leishmaniasis: what are the needs for diagnosis, treatment and control? Nat. Rev. Microbiol. 5(11supp), S7 (2007)
World Health Organization: Investing to Overcome the Global Impact of Neglected Tropical Diseases: Third WHO Report on Neglected Tropical Diseases 2015, vol. 3. World Health Organization (2015)
Alvar, J., Yactayo, S., Bern, C.: Leishmaniasis and poverty. Trends Parasitol. 22(12), 552–557 (2006)
Agyingi, E.O., Ross, D.S., Bathena, K.: A model of the transmission dynamics of leishmaniasis. J. Biol. Syst. 19(2), 237–250 (2011)
Bi, K., Chen, Y., Zhao, S., Kuang, Y., John Wu, C.-H.,: Current visceral leishmaniasis research: a research review to inspire future study. BioMed Res. Int. 2018, Article ID 9872095 (2018)
Boukhalfa, F., Helal, M., Lakmeche, A.: Mathematical analysis of visceral leishmaniasis model. Res. Appl. Math. 1, Article ID 101263 (2017)
ELmojtaba, I.M., Mugisha, J., Hashim, M.H.: Mathematical analysis of the dynamics of visceral leishmaniasis in the Sudan. Appl. Math. Comput. 217(6), 2567–2578 (2010)
ELmojtaba, I.M., Mugisha, J., Hashim, M.H.: Vaccination model for visceral leishmaniasis with infective immigrants. Math. Methods Appl. Sci. 36(2), 216–226 (2013)
Ready, P.D.: Epidemiology of visceral leishmaniasis. Clin. Epidemiol. 6, 147 (2014)
Zhao, S., Kuang, Y., Wu, C.-H., Ben-Arieh, D., Ramalho-Ortigao, M., Bi, K.: Zoonotic visceral leishmaniasis transmission: modeling, backward bifurcation, and optimal control. J. Math. Biol. 73(6–7), 1525–1560 (2016)
Biswas, S.: Mathematical modeling of visceral leishmaniasis and control strategies. Chaos Solitons Fractals 104, 546–556 (2017)
Kuang, Y.: Delay Differential Equations: With Applications in Population Dynamics, vol. 191. Academic Press, Cambridge (1993)
Wanjun, X., Soumen, K., Maitra, S.: Dynamics of a delayed seiq epidemic model. Adv. Differ. Equ. 2018(336), 1–21 (2018)
Basir, F.A.: Dynamics of infectious diseases with media coverage and two time delay. Math. Models Comput. Simul. 10(6), 770–783 (2018)
Shu, L., Weiming, Y.: Cholera model incorporating media coverage with multiple delays. Math. Methods Appl. Sci. 42(2), 419–439 (2019)
Ephraim, A., Tamas, W.: Analysis of a model of leishmaniasis with multiple time lags in all populations. Math. Comput. Appl. 24(63), 1–16 (2019)
Das, P., Mukherjee, D., Sarkar, A.: Effect of delay on the model of American cutaneous leishmaniasis. J. Biol. Syst. 15(02), 139–147 (2007)
Roy, P.K., Biswas, D., Basir, F.: Transmission dynamics of cutaneous leishmaniasis: a delay-induced mathematical study. J. Med. Res. Dev. 4(2), 11–23 (2015)
Shimozako, H.J., Wu, J., Massad, E.: Mathematical modelling for zoonotic visceral leishmaniasis dynamics: a new analysis considering updated parameters and notified human Brazilian data. Infect. Dis. Model. 2(2), 143–160 (2017)
Rihan, F.A., Rahman, D.A., Lakshmanan, S., Alkhajeh, A.: A time delay model of tumour-immune system interactions: global dynamics, parameter estimation, sensitivity analysis. Appl. Math. Comput. 232, 606–623 (2014)
Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.: On the definition and the computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28(4), 365–382 (1990)
Gu, K., Chen, J., Kharitonov, V.L.: Stability of Time-Delay Systems. Springer, Berlin (2003)
Acknowledgements
The authors would like to acknowledge financial support from Sultan Qaboos University, Oman and United Arab Emirates University, UAE through the joint research Grant No. CL/SQU-UAEU/17/01. The authors acknowledge, with thanks, the comments of an anonymous reviewer, which enhanced the clarity and readability of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Gandhi, V., Al-Salti, N.S. & Elmojtaba, I.M. Mathematical analysis of a time delay visceral leishmaniasis model. J. Appl. Math. Comput. 63, 217–237 (2020). https://doi.org/10.1007/s12190-019-01315-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-019-01315-5