Mathematical model of the immune response to dengue virus

Abstract

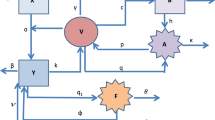
Dengue disease is caused by an infected mosquito bite and manifests in different clinical symptoms. The complexity of the pathogenesis of dengue virus and the limitations of biological knowledge have been barriers to completely understanding the progress of this disease. To address this concern, we developed a mathematical model of the immune response to eliminate dengue virus. The model considered both cellular and humoral immune responses, and we evaluated their contributions to the clearance of dengue virus.We also performed global sensitivity analysis and parameters estimation using clinical data. We found the global stability for virus-free equilibrium and for the virus-presence equilibrium, we concluded that to avoid oscillations in the model and to control the viral load, a strong proliferation of cytotoxic cells must prevail. However, if there exists a weak proliferation of cytotoxic cells, the way to avoid instabilities is to either inhibit the differentiation of T-CD4+ helper cells in Th1 cells or increase the proliferation of B cells.

Appendices

Appendices

1.1 A Genetic Algorithm

The function to be minimized is $f(V,\varUpsilon )=(V-V_{data})^{2}$, where V is the viral load, given by positive solution of the system (1)–( 4) at steady state, $V_{data}$ are the data of viral load of patients and $\varUpsilon =(\beta _{_{I}},\alpha _{v},\gamma _{1},\gamma _{2},\alpha _{r},\alpha _{a},\alpha _{cr},\alpha _{ca},\mu _{v})$ is the set of the unknown parameters, where $\beta _{_{I}}\in (\beta _{_{I}min},\beta _{_{I}max})$, $\alpha _{v}\in (\alpha _{vmin},\alpha _{vmax})$, $\ldots$, $\mu _{v}\in (\mu _{vmin},\mu _{vmax})$. The first step is the transformation of each parameter in binary and form a string called chromosome. Let $\varGamma$ be the binary representation of $\varUpsilon$. Then

$$\begin{aligned} \varGamma =(\beta _{_{I}2}\alpha _{v2}\gamma _{12}\gamma _{22}\alpha _{r2}\alpha _{a2}\alpha _{cr2}\alpha _{ca2}\mu _{v2}) \end{aligned}$$

will be the chromosome, which has just 1’s and 0’s and $\beta _{_{I}2}$, $\alpha _{v2}$, $\gamma _{12}$, $\gamma _{22}$, $\alpha _{r2}$, $\alpha _{a2}$, $\alpha _{cr2}$, $\alpha _{ca2}\ \text {and}\ \mu _{v2}$ are the binary representation of parameters. This chromosome has length $m=\sum _{i=1}^{9}m_{i}$, where $m_{1}$ is the smallest integer such that $(\beta _{_{I}max}-\beta _{_{I}min})\times 10^{p}<2^{m_{1}}-1$, $m_{2}$ is the smallest integer such that $(\alpha _{vmax}-\alpha _{vmin})\times 10^{p}<2^{m_{2}}-1$, $\dots$, $m_{9}$ is the smallest integer such that $(\mu _{vmax}-\mu _{vmin})\times 10^{p}<2^{m_{9}}-1$ and p is the number indicating decimal places desirable for the parameters. Each $m_{i}$ is the length of binary string of parameters.

The algorithm is:

• 1. Initial population

  We create a random population $P_{0}$ of chromosomes, where each chromosome is a binary string of length $m=\sum _{i=1}^{9}m_{i}$. We suppose that this initial population has n chromosomes, i.e.,

  $$\begin{aligned} P_{0}=\{\varGamma _{0}^{1},\ldots ,\varGamma _{0}^{n}\}. \end{aligned}$$

• 2. Evaluation of function

  At this step we evaluate the function f at each element of the population $P_{0}$, that is, $f(V,\varUpsilon ^{i})$, where $\varUpsilon ^{i}$ is the decimal representation of $\varGamma _{0}^{i}$, $i=1$, $\dots$, n.

• 3. Next Population

  At this step we select the next population by applying the genetic operator (crossover and mutations).

  • Selection method

    In order to select the population, we apply the tournament selection method, which consists in selecting randomly some number k of chromosome and storing the minimum of the set $\{f(V,\varUpsilon ^{J_{1}})$, $\ldots$, $f(V, \varUpsilon ^{J_{k}})\}$ of k elements, where J is a subset of k elements ($J\subset \{1,2,\ldots ,n\}$), into the next generation. This process is repeated n times. Obviously, some chromosomes would be selected more than once. Now, we apply the crossover and mutations operators to this selected population.

  • Crossover operator

    This operator apply recombination in the chromosomes (see Fig. 7). We give the probability of crossover $p_{c}$. This probability gives us the expected number $p_{c}\times n$ of chromosomes, which undergo the crossover operation. The process of crossover function is done in the following way: for each chromosome in the (new) population, we generate a random number r from the range [0, 1]. If $r<p_{c}$, we select this chromosome for crossover.

    If the number of selected chromosomes is even, we can pair them easily. If the number of selected chromosomes were odd, we would either add one extra chromosome or remove one selected chromosome, which is made randomly as well. The operator explained here is known as one-point crossover. There are other crossover operator as: two-point crossover, uniform crossover and half uniform crossover.

  • Mutation operator

    This operator applies alterations in the elements of chromosomes (changes of 0 for 1 and vice versa (see Fig. 8). We give the probability of mutation $p_{m}$. This probability gives us the expected number of mutated elements $p_{m}\times m\times _{n}$. The process to perform the mutation operator is similar to the crossover operator: for each chromosome in the current (i.e., after crossover) population and for each element within the chromosome, a random number r is generated in the range [0, 1]. If $r<p_{m}$, then we mutate the element.

• 4. After all the above steps, we have created the first generation: population $P_{1}$. Now just repeat the steps 2 and 3 to $P_{1}$, and the process goes up to the desired generations.

Fig. 7

The one-point crossover in two chromosome

Fig. 8

The mutation operator

A detailed explanation of genetic algorithms can be found in [22]. The algorithm adapted and used in the simulations can be accessed in the link http://people.csail.mit.edu/gbezerra/Code/GA/ga.m.