Skip to main content

Advertisement

Springer Nature Link
Log in

Study of the NIPG method for two–parameter singular perturbation problems on several layer adapted grids

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

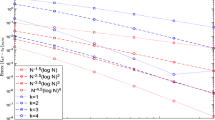
In this paper, we apply the non-symmetric interior penalty Galerkin (NIPG) method to obtain the numerical solution of two-parameter singularly perturbed convection-diffusion-reaction boundary-value problems. In order to discretize the domain, here, we use the layer-adapted piecewise-uniform Shishkin mesh, the Bakhvalov mesh and the exponentially-graded mesh. We establish a superconvergence result of the NIPG method, that is, the proposed method is parameter-uniformly convergent with the order almost \((k+1)\) on the Shishkin mesh and \((k+1)\) on the Bakhvalov mesh and on the exponentially graded mesh in the energy norm, where k is the order of the polynomials. Numerical results comparing the three different types of meshes are presented at the end of the article supporting the theoretical error estimates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Arnold, D.N.: An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 19(4), 742–760 (1982)

    MathSciNet  MATH  Google Scholar 

  2. Brdar, M., Franz, S., Roos, H.-G.: Numerical treatment of singularly perturbed fourth-order two-parameter problems. Electron. Trans. Numer. Anal. 51, 50–62 (2019)

    MathSciNet  MATH  Google Scholar 

  3. Brdar, M., Zarin, H.: A singularly perturbed problem with two parameters on a Bakhvalov-type mesh. J. Comput. Appl. Math. 292, 307–319 (2016)

    MathSciNet  MATH  Google Scholar 

  4. Chen, H.: Superconvergence properties of discontinuous Galerkin methods for two-point boundary value problems. Int. J. Numer. Anal. Model. 3(2), 163–185 (2006)

    MathSciNet  MATH  Google Scholar 

  5. Farrell, P.A., Hegarty, A.F., Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Robust Computational Techniques for Boundary Layers. Applied Mathematics, vol. 16. Chapman & Hall/CRC, Boca Raton, FL (2000)

    MATH  Google Scholar 

  6. Kadalbajoo, M.K., Yadaw, A.S.: Parameter-uniform Ritz-Galerkin finite element method for two parameter singularly perturbed boundary value problems. Int. J. Pure Appl. Math. 55(2), 287–300 (2009)

    MathSciNet  MATH  Google Scholar 

  7. Linß, T.: The necessity of Shishkin decompositions. Appl. Math. Lett. 14(7), 891–896 (2001)

    MathSciNet  MATH  Google Scholar 

  8. Linß, T.: Layer-Adapted Meshes for Reaction-Convection-Diffusion problems. Lecture Notes in Mathematics, vol. 1985. Springer, Berlin (2010)

    MATH  Google Scholar 

  9. Linß, T., Roos, H.-G.: Analysis of a finite-difference scheme for a singularly perturbed problem with two small parameters. J. Math. Anal. Appl. 289(2), 355–366 (2004)

    MathSciNet  MATH  Google Scholar 

  10. Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Fitted Numerical Methods for Singular Perturbation Problems. World Scientific Publishing Co., Inc, River Edge (1996)

    MATH  Google Scholar 

  11. Roos, H.-G., Stynes, M., Tobiska, L.: Robust Numerical Methods for Singularly Perturbed Differential Equations. Springer Series in Computational Mathematics, vol. 24, 2nd edn. Springer, Berlin (2008)

    MATH  Google Scholar 

  12. Singh, G., Natesan, S.: Superconvergence of discontinuous Galerkin method with interior penalties for singularly perturbed two-point boundary-value problems. Calcolo 55(4), 30 (2018). Art. 54

    MathSciNet  MATH  Google Scholar 

  13. Šiškin, G.I., Titov, V.A.: A difference scheme for a differential equation with two small parameters at the derivatives. Čisl. Metody Meh. Splošn. Sredy 7(2), 145–155 (1976)

    MathSciNet  Google Scholar 

  14. Zarin, H.: Exponentially graded mesh for a singularly perturbed problem with two small parameters. Appl. Numer. Math. 120, 233–242 (2017)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors wish to acknowledge the referees for providing valuable comments and suggestions.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, Assam, 781039, India

    Gautam Singh & Srinivasan Natesan

Authors
  1. Gautam Singh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Srinivasan Natesan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Srinivasan Natesan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, G., Natesan, S. Study of the NIPG method for two–parameter singular perturbation problems on several layer adapted grids. J. Appl. Math. Comput. 63, 683–705 (2020). https://doi.org/10.1007/s12190-020-01334-7

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01334-7

Keywords

Mathematics Subject Classification