Skip to main content
Springer Nature Link
Log in

A parameter-uniform collocation scheme for singularly perturbed delay problems with integral boundary condition

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

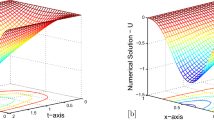
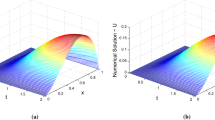
Based on the basis of B-spline functions an efficient numerical scheme on a piecewise-uniform mesh is suggested to approximate the solution of singularly perturbed problems with an integral boundary condition and having a delay of unit magnitude. For the small diffusion parameter \(\varepsilon \), an interior layer and a boundary layer occur in the solution. Unlike most numerical schemes our scheme does not require the differentiation of the problem data (integral boundary condition). The parameter-uniform convergence (the second-order convergence except for a logarithmic factor) is confirmed by numerical computations of two test problems. As a variant double mesh principle is used to measure the accuracy of the method in terms of the maximum absolute error.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Almomani, R., Almefleh, H.: On heat conduction problem with integral boundary condition. J. Emerg. Trends Eng. Appl. Sci. 3, 977–979 (2012)

    Google Scholar 

  2. Amiraliyev, G.M., Çakir, M.: Numerical solution of the singularly perturbed problem with nonlocal boundary condition. Appl. Math. Mech. (Engl. Ed.) 23, 755–764 (2002)

    Article  MathSciNet  Google Scholar 

  3. Ashyralyev, A., Sharifov, Y.A.: Existence and uniqueness of solutions for nonlinear impulsive differential equations with two-point and integral boundary conditions. Adv. Differ. Equ. (2013). https://doi.org/10.1186/1687-1847-2013-173

    Article  MathSciNet  MATH  Google Scholar 

  4. Bahuguna, D., Abbas, S., Dabas, J.: Partial functional differential equation with an integral boundary condition and applications to popoulation dynamics. Nonlinear Anal. 69, 2623–2635 (2008)

    Article  MathSciNet  Google Scholar 

  5. Bahuguna, D., Dabas, J.: Existence and uniqueness of a solution to a semilinear partial delay differential equation with an integral condition. Nonlinear Dyn. Syst. Theory 8, 7–19 (2008)

    MathSciNet  MATH  Google Scholar 

  6. Boucherif, A.: Second order boundary value problems with integral boundary condition. Nonlinear Anal. 70, 368–379 (2009)

    Article  MathSciNet  Google Scholar 

  7. Brykalov, S.A.: A second order nonlinear problem with two-point and integral boundary conditions. Georg. Math. J. 1, 243–249 (1994)

    Article  Google Scholar 

  8. Cahlon, B., Kulkarni, D.M., Shi, P.: Stepwise stability for the heat equation with a nonlocal constraint. SIAM J. Numer. Anal. 32, 571–593 (1995)

    Article  MathSciNet  Google Scholar 

  9. Çakir, M., Amiraliyev, G.M.: A finite difference method for the singularly perturbed problem with nonlocal boundary condition. Appl. Math. Comput. 160, 539–549 (2005)

    MathSciNet  MATH  Google Scholar 

  10. Cannon, J.R.: The solution of the heat equation subject to the specification of energy. Q. Appl. Math. 21, 155–160 (1963)

    Article  MathSciNet  Google Scholar 

  11. Culshaw, R.V., Ruan, S.: A delay differential equation model of HIV infection of \(CD4^+\) T-cells. Math. Biosci. 165, 27–39 (2000)

    Article  Google Scholar 

  12. Denche, M., Marhoune, A.L.: High-order mixed-type differential equations with weighted integral boundary conditions. Electron. J. Differ. Equ. 2000, 1–10 (2000)

    MathSciNet  MATH  Google Scholar 

  13. Doolan, E.P., Miller, J.J.H., Schilders, W.H.A.: Uniform Numerical Methods for Problems with Initial and Boundary Layers. Boole Press, Dublin (1980)

    MATH  Google Scholar 

  14. Ewing, R.E., Lin, T.: A class of parameter estimation techniques for fluid flow in porous media. Adv. Water Res. 14, 89–97 (1991)

    Article  MathSciNet  Google Scholar 

  15. Farrell, P.A., Hegarty, A.F., Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Robust Computational Techniques for Boundary Layers. Chapman-Hall/CRC, Boca Raton (2000)

    Book  Google Scholar 

  16. Farrell, P.A., O’Riordan, E., Shishkin, G.I.: A class of singularly perturbed semilinear differential equations with interior layers. Math. Comput. 74, 1759–1776 (2005)

    Article  MathSciNet  Google Scholar 

  17. Formaggia, L., Nobil, F., Quarteroni, A., Venezian, A.: Multiscale modelling of the circulatory system: a preliminary analysis. Comput. Vis. Sci. 2, 75–83 (1999)

    Article  Google Scholar 

  18. Gallardo, J.M.: Second order differential operators with integral boundary conditions and generation of semigroups. Rocky Mt. J. Math. 30, 1265–1292 (2000)

    Article  MathSciNet  Google Scholar 

  19. Glizer, V.Y.: Asymptotic analysis and solution of a finite-horizon \(H_{\infty }\) control problem for singularly perturbed linear systems with small state delay. J. Optim. Theory Appl. 117, 295–325 (2003)

    Article  MathSciNet  Google Scholar 

  20. Hall, C.A.: On error bounds for spline interpolation. J. Approx. Theory 1, 209–218 (1968)

    Article  MathSciNet  Google Scholar 

  21. Hu, M., Wang, L.: Triple positive solutions for an impulsive dynamic equation with integral boundary condition on time scales. Int. J. Appl. Math. Stat. 31, 43–66 (2013)

    MathSciNet  Google Scholar 

  22. Ionkin, N.I., Furletov, D.G.: Uniform stability of difference schemes for a nonlocal nonselfadjoint boundary value problem with variable coefficients. Differ. Equ. 27, 820–826 (1991)

    MathSciNet  MATH  Google Scholar 

  23. Jankowskii, T.: Differential equations with integral boundary conditions. J. Comput. Appl. Math. 147, 1–8 (2002)

    Article  MathSciNet  Google Scholar 

  24. Joseph, D.D., Preziosi, L.: Heat waves. Rev. Mod. Phys. 61, 41–73 (1989)

    Article  MathSciNet  Google Scholar 

  25. Kadalbajoo, M.K., Patidar, K.C.: \(\varepsilon \)-Uniform fitted mesh finite difference methods for general singular perturbation problems. Appl. Math. Comput. 179, 248–266 (2006)

    MathSciNet  MATH  Google Scholar 

  26. Kadalbajoo, M.K., Sharma, K.K.: Numerical treatment of boundary value problems for second order singularly perturbed delay differential equations. Comput. Appl. Math. 24, 151–172 (2005)

    Article  MathSciNet  Google Scholar 

  27. Kadalbajoo, M.K., Kumar, D.: Fitted mesh B-spline collocation method for singularly perturbed differential-difference equations with small delay. Appl. Math. Comput. 204, 90–98 (2008)

    MathSciNet  MATH  Google Scholar 

  28. Kumar, D., Kumari, P.: A parameter-uniform numerical scheme for the parabolic singularly perturbed initial boundary value problems with large time delay. J. Appl. Math. Comput. 59, 179–206 (2019)

    Article  MathSciNet  Google Scholar 

  29. Kumar, D.: A collocation method for singularly perturbed differential-difference turning point problems exhibiting boundary/interior layers. J. Differ. Equ. Appl. 24, 1847–1870 (2018)

    Article  MathSciNet  Google Scholar 

  30. Li, H., Sun, F.: Existence of solutions for integral boundary value problems of second order ordinary differential equations. Bound. Value Probl. 2012, 147 (2012). https://doi.org/10.1186/1687-2770-2012-147

    Article  MathSciNet  MATH  Google Scholar 

  31. Lomtatidze, A., Malaguti, L.: On a nonlocal boundary-value problems for second order nonlinear singular differential equations. Georg. Math. J. 7, 133–154 (2000)

    Article  MathSciNet  Google Scholar 

  32. Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Fitted Numerical Methods for Singular Perturbation Problems. World Scientific, Singapore (1996)

    Book  Google Scholar 

  33. Nicaise, S., Xenophontos, C.: Robust approximation of singularly perturbed delay differential equations by the hp finite element method. Comput. Methods Appl. Math. 13, 21–37 (2013)

    Article  MathSciNet  Google Scholar 

  34. Pao, C.V.: Numerical solutions of reaction-diffusion equations with nonlocal boundary conditions. J. Comput. Appl. Math. 136, 227–243 (2001)

    Article  MathSciNet  Google Scholar 

  35. Rahmat, A.K.: The generalized method of quasilinearization and nonlinear boundary value problems with integral boundary conditions. Electron. J. Qual. Theory. Differ. Equ. 10, 1–15 (2003)

    MathSciNet  MATH  Google Scholar 

  36. Roos, H.G., Stynes, M., Tobiska, L.: Numerical Methods for Singularly Perturbed Differential Equations, Convection–Diffusion and Flow Problems. Springer, Berlin (1996)

    Book  Google Scholar 

  37. Tzou, D.Y.: Macro-to-Microscale Heat Transfer. Taylor and Francis, Washington (1997)

    Google Scholar 

  38. Varah, J.M.: A lower bound for the smallest singular value of a matrix. Linear Algebra Appl. 11, 3–5 (1975)

    Article  MathSciNet  Google Scholar 

  39. Zarin, H.: On discontinuous Galerkin finite element method for singularly perturbed delay differential equations. Appl. Math. Lett. 38, 27–32 (2014)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Authors acknowledge their sincere thanks to the Department of Science and Technology (DST), New Delhi, India for providing support under the FIST Grant (SR/FST/MSI-090/2013(C)). The second author also thanks DST for financial support (Code No. IF160648, dated 22 August 2017). The authors are thankful to the anonymous reviewer for his/her careful reading of the manuscript and his/her valuable comments/suggestions which improved the quality of the work.

Author information

Authors and Affiliations

  1. Department of Mathematics, Birla Institute of Technology and Science, Pilani, Rajasthan, 333031, India

    Devendra Kumar & Parvin Kumari

Authors
  1. Devendra Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Parvin Kumari
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Parvin Kumari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, D., Kumari, P. A parameter-uniform collocation scheme for singularly perturbed delay problems with integral boundary condition. J. Appl. Math. Comput. 63, 813–828 (2020). https://doi.org/10.1007/s12190-020-01340-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01340-9

Keywords

Mathematics Subject Classification