Skip to main content

Advertisement

SpringerLink
Log in

Hopf and forward bifurcation of an integer and fractional-order SIR epidemic model with logistic growth of the susceptible individuals

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

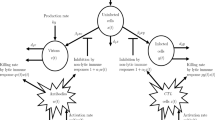
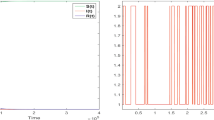
This paper deals with the qualitative behavior of an integer and fractional-order SIR epidemic model with logistic growth of the susceptible individuals. Firstly, the positivity and boundedness of solutions for integer-order model are proved. The basic reproduction number \({\mathcal {R}}_0\) is driven and it is shown that the disease-free equilibrium is globally asymptotically stable if \({\mathcal {R}}_0<1\) in integer-order model. Using the methods of bifurcations theory, it is proved that the integer-order model exhibits forward bifurcation and Hopf bifurcation. Next, with the aim of the stability theory of fractional-order systems, some conditions, which can guarantee the local stability of the fractional-order model, are developed and occurrence of forward and Hopf bifurcations in this model are studied. Lastly, numerical simulations are illustrated to support the theoretical results and a comparison between the integer and fractional-order systems is presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Ahmed, E., El-Sayed, A., El-Saka, H.A.A.: On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A 358, 1–4 (2006)

    Article  MathSciNet  Google Scholar 

  2. Aman, S., Al-Mdallal, Q., Khan, I.: Heat transfer and second order slip effect on mhd flow of fractional maxwell fluid in a porous medium. J. King Saud Univ. Sci. 32(1), 450–458 (2020)

    Article  Google Scholar 

  3. Brauer, F., Castillo-Chávez, C.: Mathematical Models in Population Biology and Epidemiology. Springer, Berlin (2001)

    Book  Google Scholar 

  4. Capasso, V., Serio, G.: A generalization of the Kermack–Mckendrick deterministic epidemic model. Math. Biosci. 42(1–2), 43–61 (1978)

    Article  MathSciNet  Google Scholar 

  5. Caponetto, R.: Fractional Order Systems: Modeling And Control Applications, vol. 72. World Scientific, Singapore (2010)

    Book  Google Scholar 

  6. Chena, Y., Zouc, S., Yang, J.: Global analysis of an sir epidemic model with infection age and saturated incidence. Nonlinear Anal. Real World Appl. 30, 16–31 (2016)

    Article  MathSciNet  Google Scholar 

  7. Dhooge, A., Govaerts, W., Kuznetsov, Y.A.: Matcont: a matlab package for numerical bifurcation analysis of odes. ACM Trans. Math. Softw. 29(2), 141–164 (2003)

    Article  MathSciNet  Google Scholar 

  8. El-Saka, H.A.A.: Backward bifurcations in fractional-order vaccination models. J. Egypt. Math. Soc. 23, 49–55 (2015)

    Article  MathSciNet  Google Scholar 

  9. El-Saka, H.A., Ahmed, E., Shehata, M.I., El-Sayed, A.M.A.: On stability, persistence, and Hopf bifurcation in fractional order dynamical systems. Nonlinear Dyn. 56(1–2), 121 (2009)

    Article  MathSciNet  Google Scholar 

  10. El-Sayed, A.M.A.: On the existence and stability of positive solution for a nonlinear fractional-order differential equation and some applications. Alex J Math 1(1), 1–10 (2010)

    Google Scholar 

  11. Ermentrout, B.: Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students, vol. 14. SIAM, New York (2002)

    Book  Google Scholar 

  12. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Book  Google Scholar 

  13. Hu, X.L., Sun, F.G., Wang, C.X.: Global analysis of sir epidemic model with the saturated contact rate and vertical transmission. Basic Sci. J. Textile Univ. 23, 120–122 (2010)

    Google Scholar 

  14. Huang, Z., Yang, Q., Cao, J.: Stochastic stability and bifurcation for the chronic state in Marchuk’s model with noise. Appl. Math. Model. 35, 5842–5855 (2011)

    Article  MathSciNet  Google Scholar 

  15. Huo, J., Zhao, H.: Dynamical analysis of a fractional sir model with birth and death on heterogeneous complex networks. Phys. A Stat. Mech. Its Appl. 448, 41–56 (2016)

    Article  MathSciNet  Google Scholar 

  16. Jana, S., Kumar Nandi, S., Kar, T .K.: Complex dynamics of an sir epidemic model with saturated incidence rate and treatment. Acta Biotheor. 64, 65–84 (2016)

    Article  Google Scholar 

  17. Li, J., Teng, Z., Wang, G., Zhang, L., Hu, C.: Stability and bifurcation analysis of an sir epidemic model with logistic growth and saturated treatment. Chaos Solitons Fract. 99, 63–71 (2017)

    Article  MathSciNet  Google Scholar 

  18. Liu, W., Hethcote, H.W., Levin, S.A.: Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biosci. 25, 359–380 (1987)

    Article  MathSciNet  Google Scholar 

  19. Liu, W., Levin, S., Iwasa, Y.J.: Influence of nonlinear incidence rates upon the behavior of sirs epidemiological models. J. Math. Biol. 23, 187–204 (1986)

    Article  MathSciNet  Google Scholar 

  20. Matignon, D.: Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 2, 963–968 (1996)

    Google Scholar 

  21. Mouaouine, A., Boukhouima, A., Hattaf, K., Yousfi, N.: A fractional order sir epidemic model with nonlinear incidence rate. Adv. Differ. Equ. 160, 1–9 (2018)

    MathSciNet  MATH  Google Scholar 

  22. Perko, L.: Rotated vector fields. J. Differ. Equ. 103(1), 127–145 (1993)

    Article  MathSciNet  Google Scholar 

  23. Podlubny, I.: Fractional Differential Equations. Academic Press, London (1999)

    MATH  Google Scholar 

  24. Rostamy, D., Mottaghi, E.: Forward and backward bifurcation in a fractional-order sir epidemic model with vaccination. Iran. J. Sci. Technol. Trans. A Sci. 42(2), 663–671 (2018)

    Article  Google Scholar 

  25. Shan, C., Zhu, H.: Bifurcations and complex dynamics of an sir model with the impact of the number of hospital beds. J. Differ. Equ. 257(5), 1662–1688 (2014)

    Article  MathSciNet  Google Scholar 

  26. Singh, J., Kumar, D., Hammouch, Z., Atangana, A.: A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 316, 504–515 (2018)

    MathSciNet  MATH  Google Scholar 

  27. Tavazoei, M.S., Haeri, M.: A proof for non existence of periodic solutions in time invariant fractional order systems. Automatica 45(8), 1886–1890 (2009)

    Article  MathSciNet  Google Scholar 

  28. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of diseases transmission. Math. Biosci. 180, 29–48 (2002)

    Article  MathSciNet  Google Scholar 

  29. Wang, W., Ruan, S.: Bifurcation in an epidemic model with constant removal rate of the infectives. J. Math. Anal. Appl. 291, 775–793 (2004)

    Article  MathSciNet  Google Scholar 

  30. Wang, Z., Wang, X., Li, Y., Huang, X.: Stability and hopf bifurcation of fractional-order complex-valued single neuron model with time delay. Int. J. Bifurc. Chaos 27(13), 1750209 (2017)

    Article  MathSciNet  Google Scholar 

  31. Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos, vol. 2. Springer, Berlin (2003)

    MATH  Google Scholar 

  32. Zhang, X., Liu, X.: Backward bifurcation of an epidemic model with saturated treatment. J. Math. Anal. Appl. 348, 433–443 (2008)

    Article  MathSciNet  Google Scholar 

  33. Zhou, L., Fan, M.: Dynamics of an sir epidemic model with limited medical resources revisited. Nonlinear Anal. Real World Appl. 13(1), 312–324 (2012)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Yazd University, Yazd, Iran

    M. H. Akrami

  2. Department of Mathematics, Razi University, Kermanshah, Iran

    A. Atabaigi

Authors
  1. M. H. Akrami
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Atabaigi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. H. Akrami.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Akrami, M.H., Atabaigi, A. Hopf and forward bifurcation of an integer and fractional-order SIR epidemic model with logistic growth of the susceptible individuals. J. Appl. Math. Comput. 64, 615–633 (2020). https://doi.org/10.1007/s12190-020-01371-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01371-2

Keywords

Mathematics Subject Classification

Search

Navigation