Abstract
This work is considered in the framework of studies dedicated to the control problems, especially in epidemiology where the scientist are concerned to develop effective control strategies to minimize the number of infected individuals. In this paper, we set this problem as an asymptotic target control problem under mixed state-control constraints, for a general class of ordinary differential equations that model the temporal evolution of disease spread. The set of initial data, from which the number of infected people decrease to zero, is generated by a new type of Lyapunov functions defined in the sense of viability theory. The associated controls are provided via selections of adequately designed feedback map. The existence of such selections is improved by using Micheal selection theorem. Finally, an application to the SIRS epidemic model, with numerical simulations, is given to show the efficiency of our approach. To the best of our knowledge, our work is the first one that used a set-valued approach based on the viability theory to deal with an epidemic control problem.
Keywords: Non-linear control systems, Epidemic models, Lyapunov functions, Viability theory, Contingent cone, Selections
Introduction and problem statement
Infectious diseases have marked the history of human societies. Throughout the centuries and the world, they have always been the leading cause of death. One thinks of the great plagues of the Middle Ages which emptied cities of their populations and caused urban civilization to regress (a third of the European population disappeared between the end of the fourteenth and the beginning of the fifteenth century [1]). The viruses imported into America by the Spaniards which decimated the local populations more surely than the fights. The Spanish flu which caused more deaths at the beginning of the twentieth century than the First World War. The Acquired Immunodeficiency Syndrome, better known under its acronym AIDS, which is still the most deadly infectious disease in the world, and which has claimed nearly 25 million victims since its appearance in 1981. We also think of the Coronavirus disease (Covid-19), which is now considered as a global pandemic.
To counter the ravages that infectious diseases can cause, public health decision-makers must have relevant tools to assist them in their decision-making. In this context, mathematicians, epidemiologists and immunologists have been working together for quite some time to create mathematical models that allow competent authorities to prepare in advance to respond quickly and effectively if an outbreak occurs.
The first model was developed by Daniel Bernoulli in 1760 for smallpox [2]. But, the foundations of the epidemic modelling based on the compartmental models were established by Sir Ronald Ross, W. H. Hamer, W. O. Kermack and others. In these models, the population is divided into classes that contain individuals with the same epidemiological status. An interesting overview of the history of mathematical models in epidemiology can be found in [3–6]. Currently, epidemiological models are increasingly used and present a powerful tool for studying complex systems. Its contribution to the fight against epidemics is indisputable. It enables us to understand the mechanisms of transmission, to study the characteristics of an epidemic, to predict its evolution and to evaluate different intervention strategies to find the best control program.
In the literature, several works have addressed the problems of controlling the spread of infectious diseases based on epidemiological models with compartments. Di Giamberardino and Iacoviello [7] proposed an epidemic control problem based on a three compartments model and a vaccination strategy with a cost index that weights differently the control depending on the severity of the disease. Buonomo et al. [8] focus on an epidemic model which incorporates a non-linear force of infection and two controls: an imperfect preventive vaccine given to susceptible individuals and treatment given to infectious. Work done by Zakary et al. [9], devise a discrete time compartment model depicting the spread of infectious diseases in various geographical regions that are connected by any kind of anthropological movement. The authors used two control variables which represent the effectiveness rates of vaccination and travel-blocking operation, and they focus to control the outbreaks of an epidemic that affects a hypothetical population belonging to a specific region. Another work that concerns the control of the Ebola virus disease was proposed by Mhlanga [10]. The mathematical model includes control functions representing educational campaigns in their respective patches, with one patch having more effective controls than the other. Moualeu et al. [11] presented a deterministic model for the transmission dynamics of Tuberculosis in the context of weak diagnosis capacity. Optimal control theory is used to obtain a cost-effective balance of two different intervention methods. Degang et al. [12] presented a novel SIVRS mathematical model for infectious diseases, which takes into account the virus variation factors. Authors proposed an optimal control problem to maximize the recovered agents with the limited resource allocation. Existence of a solution to the optimal control problem is given based on Pontryagin’s Minimum Principle. Bolzoni et al. [13] proposed a problem of minimizing epidemic size and duration in SIR models. Optimal control through either vaccination or isolation is investigated by application of Pontryagin’s Maximum Principle. Using a basic SEI model with saturated incidence rate, Baba et al. [14] studied the effect of optimal controller and awareness on the dynamic of Tuberculosis. In these works and in many others (see [15–20] and the references therein) the authors have solved the formulated control problems using classical results of control theory, in particular the famous Pontryagin’s minimum principle [21].
In this paper, we propose an alternative approach which is direct and allows characterizing one or more controls aimed at achieving the null number of infected people at a final time. Our approach is based on viability theory [22], which allows the adaptation of the evolution of a dynamic system to the restrictions imposed on the state and the control. We are interested here in compartment models that represent the evolution of an infectious disease in a population, which are written as follows
| 1a |
| 1b |
with initial conditions
| 1c |
for an integer n and where the ’s denotes the number of individuals in a population such as susceptible and recovered, while y denotes the number of infected individuals. Therefore, the state (x, y) evolves in the subset
and the control u takes values within constraints subset
| 2 |
where are positive numbers and p an integer. Both functions f and map into and respectively, and they are sufficiently smooth. Then, our control problem is stated as follows
Problem: For all , find a control such that:
| 3a |
| 3b |
| 3c |
where denotes a solution of system (1) for control .
The problem (3) has been treated by Kassara [23] and Kassara and Moustafid [24] in the framework of the set-valued approach for a class of ODE immunotherapy models. Such models was expressed by a non-linear control system (1), in the particular case, where the dynamics f (1a) is affine in control u, and the Eq.(1b) is given as follows
| 4 |
Although the approach proposed by the authors can be used for several models of cancer treatment, it is not appropriate for a large class of models where the state y can be controlled to zero by acting on its dynamics directly, especially for epidemic models, see for instance [25, 26].
Inspired by the work done in [27], we provide a unified set-valued approach in order to deal with the problem (3) for a more general class of ODE systems, where f can be non-affine with respect to the control and the dynamics depend on the control variable. More precisely, our contribution here is to seek conditions under which, any Lyapunov function (defined independently from dynamics , in a sense specified below) can generate a domain and a closed-convex valued multifunction in such a way the controls that solves the problem (3) from are given via selections of multifunction .
Such Lyapunov functions consist of real-valued functions defined on and satisfying
| 5 |
Note such functions depend only upon subset , we thereby call them -Lyapunov functions. This type of functions was firstly introduced in [27] dealing with constrained asymptotic null-controllability.
Our approach takes advantage of the unified framework of viability theory [28] and set-valued analysis [29, 30]. The main advantage is that for any initial data starting from the state stays in this region overcoming the concern mentioned in (3c). This is due to the fact that, the multifunction of regulation includes the tangential condition for viability. Even when initial data start outside the region it is possible to reach it in a certain instant. Moreover, it is of interest to stress that in the case of convex constraints, the multifunction bring us an explicit continuous selections and universal formula, notably the minimal selection despite its discontinuity. Another advantage is that this set-valued framework can be considered as a unified setting for dealing with problem (3) for an important class of ODE models including, for instance, both cancer and epidemic models.
Throughout the paper, the inner product on Euclidean space is denoted  , and corresponding norm
, and corresponding norm  . For a vector z we denote by its component. Let T be a linear operator and we denote its adjoin operator by and its norm by .
. For a vector z we denote by its component. Let T be a linear operator and we denote its adjoin operator by and its norm by .
Also, we consider the notation
The remainder of the paper is structured as follows: In Sect. 2 we provide some notations and preliminary lemmas. Section 3 will be devoted to presenting our control set-valued approach, then Sect. 4 to prove the existence of continuous selections under sufficient conditions. To show the efficiency of our approach we propose, in Sect. 5, an application to a controlled SIRS epidemic model. We conclude this paper in Sect. 6.
Definitions and preliminary results
In this section, we present some viability concepts and mathematical tools to be used next.
Let K be a nonempty subset of an Euclidean space . The contingent cone to subset K at point is defined by
where It is useful to note the following properties of the contingent cones:
If , the interior of K, then .
is closed for each .
If K is convex, then is convex for each .
If K is closed and convex then the map from K to subsets of is lsc.
In (d) above, the short-term lsc means that multifunction is lower semi-continuous, i.e. for every and any sequence of elements of K converging to x, it holds that:
for each , there exist a sequence that converges to y.
Next we provide a result which is fundamental for building our control strategy. In [29] the authors gave a useful characterization of the contingent cone in case of subsets defined by inequalities:
Lemma 1
Let be a differentiable mapping for an integer N. Given a closed convex subset K of and let and . Suppose that there exists such that , then
| 6 |
where denotes the differential operator of .
Let and consider the following system:
| 7 |
The subset D is said to be locally viable under system (7), if for all there exist and a solution to system (7), on such that for all .
The following lemma gives us sufficient conditions, in terms of contingent cones, for which the property above holds true:
Lemma 2
Assume that function is continuous on the closed subset D. Then D is locally viable under system (7) if and only if the following tangential condition holds,
| 8 |
The global solution of the system (7) is provided by using the notion of linear growth. A smooth function mapping a subset D of into is said to be of linear growth on subset D, if there exists a constant such that
However, such a condition is not required when the subset D is bounded, or when the function is bounded on this subset.
By selection of a multifunction Q it is meant a function such that for all x. We cite at this opportunity the famous Michael selection theorem [30] which will be repeatedly used in the paper:
Lemma 3
If a multifunction Q is lsc and has closed convex values, then for all such that , there exists a continuous selection of Q which satisfies .
The minimal selection (well defined if Q has closed convex values) of the map Q is given by
| 9 |
Here stands for the operator of best approximation that is defined on K as follows:
It is of interest to notice that the minimal selection is rarely continuous, see [30].
Next, given the control system
| 10 |
where v takes values in and denotes the control, , and stands for the set-valued map of constraints, define the feedback map
| 11 |
Assume that and are continuous on D, then any continuous selection of the feedback map provides a control law that leads to a viable solution to system (10) in D. This is so for minimal selection whenever it is continuous. Otherwise we may use [28, Theorem 4.3.2] as follows:
Lemma 4
Assume that the feedback map is lsc with closed convex values. Then system (10) with feedback control has a locally viable solution in D.
A control set-valued approach
In this section, we restate the problem (3) in the context of viability theory and set-valued analysis. Throughout the paper the control system (1) is assumed to satisfy the permanently hypotheses below:
For the sake of conciseness, the elements of our control strategy proceeds as follows:
-
(i)
Let be an -Lyapunov function in the sense of (5).
-
(ii)Set
and12
where denotes the mapping13 -
(iii)Define the feedback map given for each as follows
where the control v has values in closed subset14
with stands for a positive number. -
(iv)
Pick up a continuous selection of the map .
Consequently, we are ready to prove the following result:
Theorem 1
Any continuous selection of the map provides a solution of the problem (3) for each .
Proof
Let g be such a selection. Then, , the following tangential condition holds
According to lemma (2), the following system
| 15 |
has a solution which is viable in , for each . This solution is global as both f and possess linear growth and g is bounded. It follows that has values in and satisfies for all t. Then, thanks to (5), when , and thereby and satisfy condition (3a) and (3b) respectively.
In consequence, we are led to design the feedback map of Eq. (14). For that purpose we need first to compute the contingent cone . In all what follow, we assume that both
Set then for all
| 16 |
It follows that subset given by (12) can be written as
| 17 |
Using [29, Chapter 4] on tangent cones, we get the contingent cone of subset as follows
| 18 |
for all where
| 19 |
and
| 20 |
Moreover, we can easily see that the qualification condition in Lemma 1 is satisfied whenever the following conditions hold:
| 21 |
In the following result, we provide an expression of the contingent cone .
Lemma 5
Suppose that condition (21) is satisfied. Then, for each , we have
| 22 |
Proof
Thanks to Lemma 1 and condition (21), we can get easily the expression (22).
Note that the partial differentials of are given on by
| 23 |
| 24 |
and
| 25 |
Subsequently, we need to define the following functions and maps,
| 26 |
| 27 |
and
| 28 |
for all In addition, we consider the assumption
| 29 |
for .
Then, we are ready to determine a useful expression of the feedback map given by (14).
Lemma 6
Under condition (21) and (29), we have for all
| 30 |
Proof
According to (14) and Lemma 5, we get
| 31 |
for each . Thanks to (19), (20) and (29), it follows that
| 32 |
By considering (26), (27) and (28), we can see easily that the last expression is equivalent to (30).
In what follow, we provide a result for which the problem (3) has a solution from the whole domain . For this end, we need to introduce the following map, for each
| 33 |
for each
Theorem 2
Assume that, for some , the map given by (33) has a continuous selection, then problem (3) has a solution for each .
Proof
Let g be such a selection of the map . As condition (21) is satisfied, this map has values included in Then the selection g is also a continuous selection of . By Theorem 1, Problem (3) has therefore solution from . The rest of the proof is devoted to show that problem (3) has solution from .
Now, let belong to . Thereby , for all u such that . Condition (29) implies that for all . Since g(x, y, u) belongs to , then . It follows that system
admits a -viable solution (on horizon as the couple possess linear growth and g is bounded), for all such that . Let such be given, we readily have
which yields, according to Eqs. (26) and (27),
Whence
Since g is also a continuous selection of , then
Thereby
Let , and .
As a result, the use of Theorem 1 implies that system
has a solution on horizon , which ranges in and satisfies
Consequently, the control given by on and on , achieves the problem stated in (3) from .
On the existence of continuous selection
This section involves the sufficient conditions we need in order to prove the existence of continuous selection of the map as required in Theorem 2. For that purpose we will mainly use the Micheal selection theorem cited in section 2 and we assume that
Definition 1
Let . We say that -Lyapunov function belongs to subset whenever, for all , there exists which satisfies the following statement
| 34 |
where functions and are respectively given in (26) and (27).
Then we can state the following result.
Lemma 7
Let and assume that , then both maps and , as given, respectively, by (33) and (30) are lsc with closed-convex valued. (note ).
Proof
It is obvious that and are closed convex valued.
To prove that is lsc, we will rewrite it in the context of [29, Proposition 1.5.2] in the form
where for each , we have
Therefore, we can easily verify the hypotheses of the cited proposition as follows:
The map is lsc with convex values.
is continuous.
For all the mapping is affine.
For all (x, y, u), is convex and its interior is nonempty.
The graph of the map is open.
For all there exists such that
Thanks to assumption (34), the condition (6) is satisfied. Then the map is lsc.
Now we prove that is lsc.
Let be a sequence of that converge to and . We have to look for a sequence that satisfies
| 35 |
Suppose that . Since the function is continuous and we can consider the smallest number such that
Then the sequence defined by
where
merely satisfies (35) due to the fact that whenever Now assume that , then . Since the map is lsc, it follows that there exists a sequence such that for each n and . According to (30) we get for all n, as required in (35).
Lemma 8
Let and belong to , then the minimal selection of the map is continuous.
Proof
By Lemma 7 the map is lsc. Then we can use [31, Theorem 4.1] by verifying that the subset
is closed in for all . Indeed, let be a sequence in which converges to . Then there exists a sequence such that
| 36 |
for all n. Now, as is bounded it has a subsequence which converges to . Then by noting that and are continuous and letting in (36), we get
This implies that and therefore is closed.
Then we are in a position to state and prove the following result.
Theorem 3
Let and belong to . If then problem (3) has solution from , or else it has solution from the whole domain .
Proof
Suppose that and Let , then, by virtue of Lemma 7, the feedback map is lsc on and has a closed convex valued. Furthermore, Lemma 3 implies that has a continuous selection g. We are now able to use Theorem 1 to conclude that problem (3) has solution from .
Now assume that , then, the map is lsc and has a closed convex valued (By Lemma 7). As a result the Michael selection theorem (as stated in Lemma 3) yields a continuous selection g of the map . The proof ends by using Theorem 2.
The minimal selection of the map of (30) is given for all by the expression
| 37 |
where the map is given by Eq. (28). Although mapping is discontinuous, we will see in the next result that it can lead to a slow control law which solve the problem (3).
Theorem 4
Let belong to , then for all , system
| 38 |
has a solution which satisfies at infinity.
Proof
By Lemma (7), the map is lsc with closed-convex valued. Then using Lemma (4), system (38) has a solution over a bounded horizon. Since the couple has a linear growth and is bounded, then the solution can be extended to infinite horizon. Moreover, since is an -Lyapunov function, then goes to zero at infinity.
Application to a controlled SIRS epidemic model
The aim of this section is to apply the approach developed in the previous sections to an epidemic model that includes control terms. We consider a deterministic Susceptible-Infected-Recovered-(re)Susceptible (SIRS) model, where the total population, denoted N, is divided into three compartments:
Susceptible (S): healthy individuals who can become infected as a result of their interactions with infected individuals;
Infectious (I): individuals who are infected with the disease and are able of transmitting the infection to susceptible individuals;
Recovered (R): individuals who were previously infected and recover.
The SIRS model is widely used to model several diseases, such as influenza and malaria, which confer temporary immunity; the recovered individuals lose immunity after a while and become susceptible again. This model is formulated based on the following assumptions
The disease incubation is negligible, in this case, once infected, each susceptible individual becomes infectious instantaneously;
All recruitment is into the susceptible compartment and occur at a constant rate ;
The natural death rate, denoted a, is constant across all compartments;
The disease is assumed to be fatal for infectious individuals, that is why we define additional death rate c;
The transmission of the disease occurs following an adequate contact between a susceptible and infectious. Due to the non-linear contact dynamics in the population, we use the incidence function to indicate successful transmission of the disease, where b denotes the effective contact rate with infectious individuals in compartment I;
The rate of loss of immunity is e;
The population size is constant.
The dynamics of our model is governed by the following non-linear system
| 39 |
with and .
It is well known that treatment, education and awareness campaign are an important and effective method to control and prevent the spread of various epidemics. Hence, we investigate the impact of these control measures on the spread of an infectious disease by introducing in the system (39) two controls and such as
: represents the effort of preventing susceptible individuals from becoming infectious individuals. This effort includes awareness program, isolation and any other distancing measurement that can limit contacts between susceptible and infectious people;
: represents screening and treatment efforts.
So our model with controls is given by
| 40 |
with
Let , and . We can see that the model (40) satisfies the general form given by system (1), with the dynamic (1a) given as follows
| 41 |
and the infectious dynamic (1b) is given by
| 42 |
for each , where
It can be easy to see that both functions f and are differentiable. In addition, the condition (29), which gives us the positivity of the model’s solutions, is also satisfied. On the other hand, the global solution exist since both dynamics f and are bounded. In this case, the condition of linear growth is not required.
A convenient -Lyapunov function , defined in (5) and which satisfies condition (21), can be given by
Indeed, if a function satisfies: for all t, then
Using a simple Gronwall inequality, we get at infinity. Now let us express the function of (16) we get
and let and
To show the efficiency of our approach we consider three scenarios. For each scenario and in order to compute the regulation map as expressed in Eq. (33) we first give expressions of the functions and , given respectively by Eq. (26) and (27).
All simulations are performed using MATLAB with parameter values given in Table 1. The numerical results are obtained for several initial conditions corresponding to both cases where and . It should be noted that refers to when the disease starts to spread in the population, a large part of the population is healthy and the number of infections has not yet peaked. is devoted to describing an advanced stage of the epidemic where the number of infected people is quite large. For the first case, where , we use the five initial conditions (3500, 5500, 11, 000), (3000, 5000, 12, 000), (2500, 4500, 13, 000), (2000, 4000, 14, 000) and (1500, 3500, 15, 000). In the second case, the initial values are chosen as follows: (3500, 5500, 11, 000), (3000, 5000, 12, 000), , (2000, 4000, 14, 000) and (1500, 3500, 15, 000).
Table 1.
Parameters description and values
First scenario: prevention
Given the major role of contact in transmitting infectious disease from infectious individuals to susceptible people and the importance of prevention programs in limiting the number of new cases, we propose a control strategy based on the control , whereas the control is set to zeros. In this case, the expressions of functions and are given by
| 43 |
| 44 |
Then the continuous selection, of the map , that provides a solution of the problem (3) can be expressed as
| 45 |
with if and otherwise.
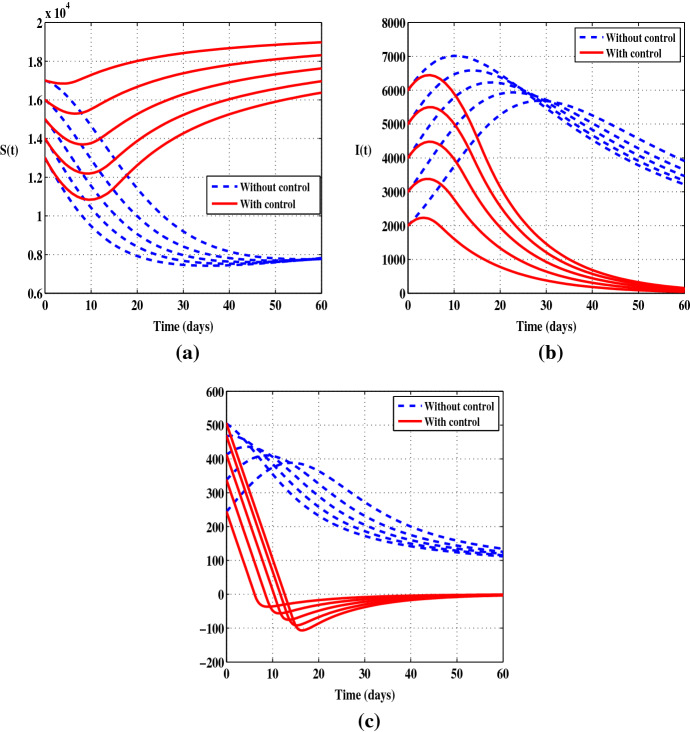
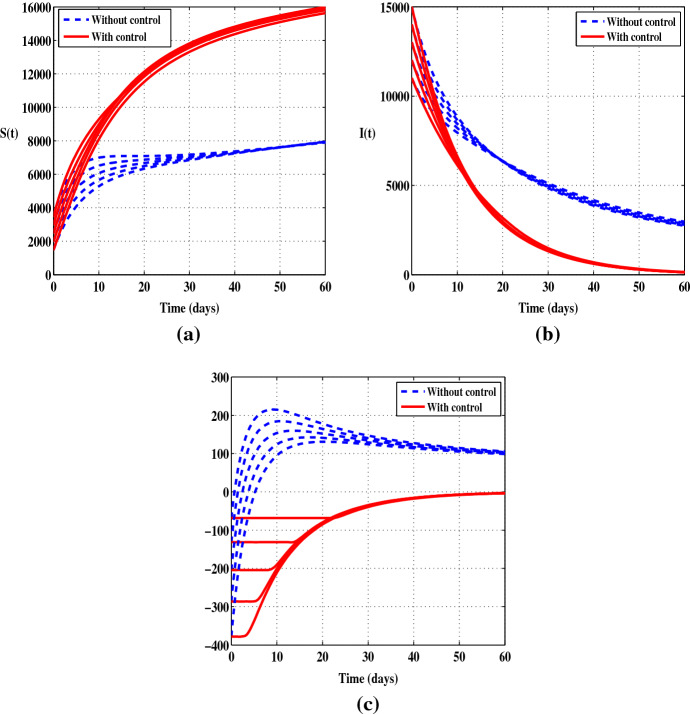
In Figs. 1 and 2 we depict the evolution over time of the susceptible individuals S, the infected individuals I and the function in the uncontrolled case and when the control is considered. We use several initial values and we consider both cases and . In Fig. 1a, it is observed that the number of S decreases sharply when there is no control, while in presence of the control we notice that there is a decrease only during the first ten days and then the number of the susceptible individuals starts to increase. Figure 1b shows a constant increase in the number of infected persons during the first few days followed by a slight decrease when there is no control, but at the end of the control period we can see a clear difference between the case with and without control. In Fig. 2a, b, it can be seen that the prevention control significantly reduces the number of infected people and increases the number of healthy people. The solutions show a decrease in the number of infections of up to at the end of the control period. Also, it should be noted that the control has a great impact on the dynamics of the function . Indeed, when the control leads the function to be negative from a certain time . Otherwise, when the function remains negative during the full control period.
Fig. 1.
Cases when the control is applied alone with five initial conditions and . a Susceptible individuals (S). b Infected individuals (I). c The function
Fig. 2.
Case when the control is applied alone with five initial conditions and . a Susceptible individuals (S). b Infected individuals (I). c The function
Second scenario: screening and treatment
In this case, we propose to provide a treatment for the infected people and facilitate the access to therapeutic programs. Thus, in this scenario we set to zero and we consider only the control . The expressions of functions and are given by
| 46 |
| 47 |
Thereby the continuous selection of the map is given by
| 48 |
with if and otherwise.
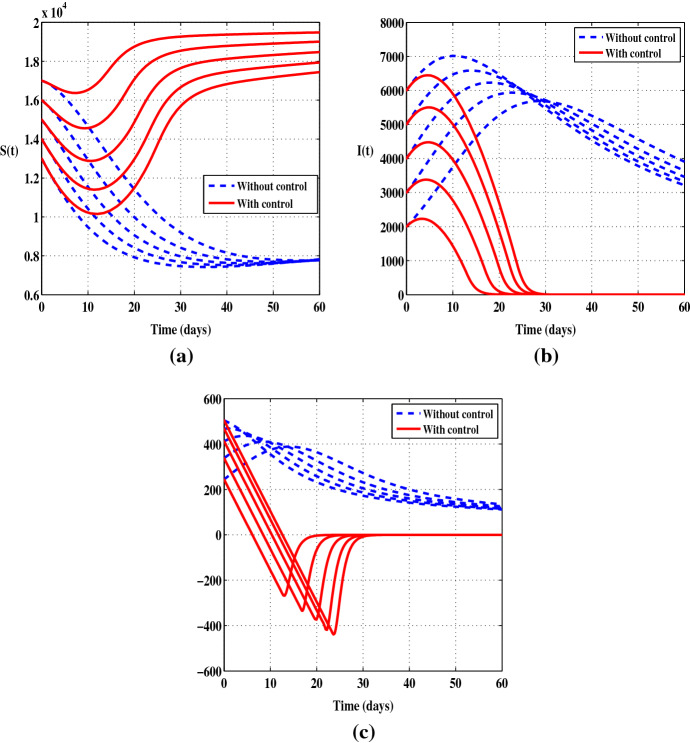
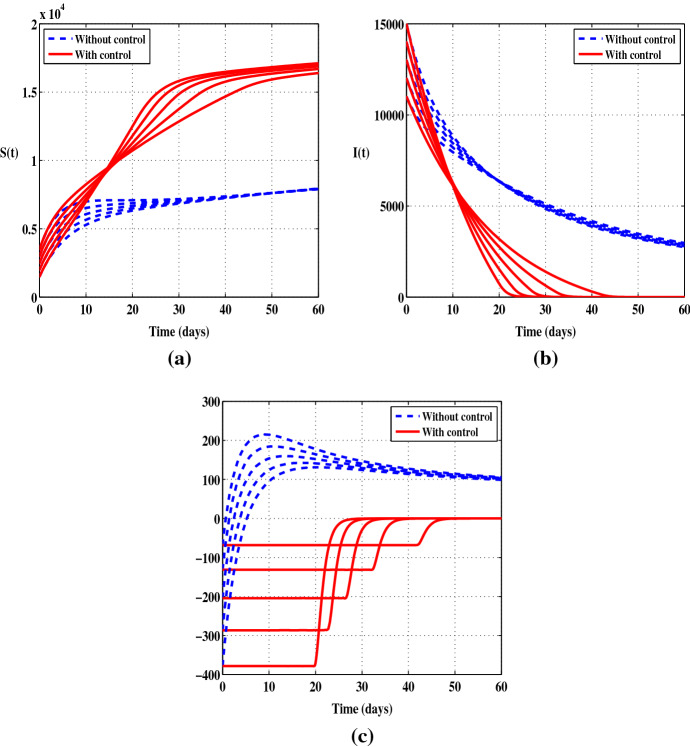
Figures 3 and 4 display the solutions of S, I and , without control and when only the control is applied. Compared to the uncontrolled case, there is a steady decrease in the number of the infected individuals. At the end of the control period, the number of I decreases by . With this scenario, we observe a clear decrease in the number of infections from the beginning of the control program whereas in the first scenario there is certainly a regression in the number of infections but more slowly. So in terms of reducing the number of I, the control is a more effective way of eliminating the disease than . Also, it should be noted that the control has the same effect on the function as the control .
Fig. 3.
Cases when the control is applied alone with five initial conditions and . a Susceptible individuals (S). b Infected individuals (I). c The function
Fig. 4.
Case when the control is applied alone with five initial conditions and . a Susceptible individuals (S). b Infected individuals (I). c The function
Third scenario: combining prevention and treatment
Let us now investigate the effect of combining all controls. With this approach none of the controls is set to zero. In this case, the expressions of functions and are given by
| 49 |
| 50 |
Then the continuous selection, of the , that provides a solution of the problem (3) can be expressed as
| 51 |
where,
with if and otherwise.
With this scenario, our results show that combining treatment and prevention measurements can lead to a decrease in the number of infected individuals, an illustrative example is given in Fig. 5a, b. Here, the major advantage of this combination is that less treatment effort is required when it is accompanied by preventive measures. One can observe a significant difference in when it is used alone (Fig. 6a) and when it is used with (Fig. 6b). It can be inferred that in some cases where screening and treating infectious individuals can be more expensive, good preventive measurements with less effort of treatment can also reduce the number of infected people.
Fig. 5.
Infected individuals without control and when controls and are all used. a Case . b Case
Fig. 6.
The control when used alone and when it is coupled with . a The control when used alone. b The control when combined with
Finally, the results obtained in this application to the SIRS model show the effectiveness of our approach. In the three proposed scenarios, we note that the control terms obtained, allow the number of infected people to tend to zero at a finite time.
Conclusion and future research
This work contributes to a growing literature on controlling epidemics spread. We have proposed a unified approach based on viability theory and set-valued analysis to deal with a control problem of a general class of epidemiological models. We have established theoretical results that show the existence and give the expression of continuous selections used to characterize our controls. The great interest of our approach is the simplicity of deriving the explicit formulas of the controls via continuous selections of adequately designed regulation map, unlike to the optimal control approach, which requires showing the existence of the optimal solution (control and state), and solving the optimality system consisting of the state system and the adjunct system that can be hard to solve. As an application, we considered a SIRS epidemic model with two controls whose expressions are given via selections of appropriately designed feedback map. These controls proved effective in reducing the number of infected individuals, either when used separately or when used together. Finally, as natural direction for our future works, we will propose extensions of our method to a class of epidemiological models where the dynamics are non-affine with respect to the control variable and also to control problems in the case of spatiotemporal epidemic models.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Didier, R.: Les nouveaux risques infectieux: SRAS, grippe aviaire, et après?. Lignes de repères (2005)
- 2.Bernoulli, D.: Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir. Histoire de l’Acad. Roy. Sci.(Paris) avec Mém. des Math. et Phys. and Mém, pp. 1–45 (1760)
- 3.Hethcote HW. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. doi: 10.1137/S0036144500371907. [DOI] [Google Scholar]
- 4.Keeling MJ, Rohani P. Modeling infectious diseases in humans and animals. Princeton University Press. 2008;42(4):599–653. [Google Scholar]
- 5.Brauer F. Mathematical epidemiology: past, present, and future. Infect. Dis. Model. 2017;2(2):113–127. doi: 10.1016/j.idm.2017.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Foppa IM. A Historical Introduction to Mathematical Modeling of Infectious Diseases: Seminal Papers in Epidemiology. Cambridge: Academic Press; 2016. [Google Scholar]
- 7.Di Giamberardino P, Iacoviello D. Optimal control of SIR epidemic model with state dependent switching cost index. Biomed. Signal Process. Control. 2017;31:377–380. doi: 10.1016/j.bspc.2016.09.011. [DOI] [Google Scholar]
- 8.Buonomo B, Lacitignola D, Vargas-De-León C. Qualitative analysis and optimal control of an epidemic model with vaccination and treatment. Math. Comput. Simul. 2014;100:88–102. doi: 10.1016/j.matcom.2013.11.005. [DOI] [Google Scholar]
- 9.Zakary O, Rachik M, Elmouki I. On the analysis of a multi-regions discrete SIR epidemic model: an optimal control approach. Int. J. Dyn. Control. 2017;5(3):917–930. doi: 10.1007/s40435-016-0233-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mhlanga A. Dynamical analysis and control strategies in modelling Ebola virus disease. Adv. Differ. Equ. 2019;2019(1):458. doi: 10.1186/s13662-019-2392-x. [DOI] [Google Scholar]
- 11.Moualeu DP, Weiser M, Ehrig R, Deuflhard P. Optimal control for a tuberculosis model with undetected cases in Cameroon. Commun Nonlinear Sci. 2015;20(3):986–1003. doi: 10.1016/j.cnsns.2014.06.037. [DOI] [Google Scholar]
- 12.Xu D, Xu X, Xie Y, Yang C. Optimal control of an SIVRS epidemic spreading model with virus variation based on complex networks. Commun Nonlinear Sci. 2017;48:200–210. doi: 10.1016/j.cnsns.2016.12.025. [DOI] [Google Scholar]
- 13.Bolzoni L, Bonacini E, Della Marca R, Groppi M. Optimal control of epidemic size and duration with limited resources. Math. Biosci. 2019;315:108232. doi: 10.1016/j.mbs.2019.108232. [DOI] [PubMed] [Google Scholar]
- 14.Baba IA, Abdulkadir RA, Esmaili P. Analysis of tuberculosis model with saturated incidence rate and optimal control. Physica A. 2020;540:123237. doi: 10.1016/j.physa.2019.123237. [DOI] [Google Scholar]
- 15.Abouelkheir I, El Kihal F, Rachik M, Elmouki I. Optimal impulse vaccination approach for an SIR control model with short-term immunity. Mathematics. 2019;7(5):420. doi: 10.3390/math7050420. [DOI] [Google Scholar]
- 16.Berge T, Ouemba Tasse AJ, Tenkam HM, Lubuma J. Mathematical modeling of contact tracing as a control strategy of Ebola virus disease. Int. J. Biomath. 2018;11(07):1850093. doi: 10.1142/S1793524518500936. [DOI] [Google Scholar]
- 17.Tan, J., Zou, X.: Optimal control strategy for abnormal innate immune response. Comput. Math. Methods Med. 2015 (2015) [DOI] [PMC free article] [PubMed]
- 18.Gubar, E., Zhu, Q., Taynitskiy, V.: Optimal control of multi-strain epidemic processes in complex networks. In: International Conference on Game Theory for Networks, pp. 108–117 (2017)
- 19.Omondi EO, Orwa TO, Nyabadza F. Application of optimal control to the onchocerciasis transmission model with treatment. Math. Biosci. 2018;297:43–57. doi: 10.1016/j.mbs.2017.11.009. [DOI] [PubMed] [Google Scholar]
- 20.Pongsumpun P, Tang IM, Wongvanich N. Optimal control of the dengue dynamical transmission with vertical transmission. Adv. Differ. Equ. 2019;2019(1):176. doi: 10.1186/s13662-019-2120-6. [DOI] [Google Scholar]
- 21.Pontryagin LS. Mathematical Theory of Optimal Processes. London: Routledge; 2018. [Google Scholar]
- 22.Aubin JP, Bayen AM, Saint-Pierre P. Viability Theory: New Directions. Berlin: Springer; 2011. [Google Scholar]
- 23.Kassara K. A unified set-valued approach to control immunotherapy. SIAM J. Control Optim. 2009;48(2):909–924. doi: 10.1137/07070591X. [DOI] [Google Scholar]
- 24.Kassara K, Moustafid A. Angiogenesis inhibition and tumor-immune interactions with chemotherapy by a control set-valued method. Math. Biosci. 2011;231(2):135–143. doi: 10.1016/j.mbs.2011.02.010. [DOI] [PubMed] [Google Scholar]
- 25.Gaff H, Schaefer E. Optimal control applied to vaccination and treatment strategies for various epidemiological models. Math. Biosci. Eng. 2009;6(3):469. doi: 10.3934/mbe.2009.6.469. [DOI] [PubMed] [Google Scholar]
- 26.Kumar A, Srivastava PK. Vaccination and treatment as control interventions in an infectious disease model with their cost optimization. Commun. Nonlinear Sci. Numer. Simul. 2017;44:334–343. doi: 10.1016/j.cnsns.2016.08.005. [DOI] [Google Scholar]
- 27.Boujallal L, Kassara K. State-input constrained asymptotic null-controllability by a set-valued approach. IET Control Theory Appl. 2015;9(15):2211–2221. doi: 10.1049/iet-cta.2014.1333. [DOI] [Google Scholar]
- 28.Aubin JP. Viability Theory. Berlin: Springer; 2009. [Google Scholar]
- 29.Aubin JP, Frankowska H. Set-Valued Analysis. Berlin: Springer; 2009. [Google Scholar]
- 30.Deimling K. Multivalued Differential Equations. Berlin: Walter de Gruyter; 2011. [Google Scholar]
- 31.Gutev V, Nedev S. Continuous selections and reflexive Banach spaces. Proc. Am. Math. Soc. 2001;129(6):1853–1860. doi: 10.1090/S0002-9939-00-05740-3. [DOI] [Google Scholar]
- 32.Rachah, A., Torres, D. F.: Modeling, dynamics and optimal control of Ebola virus spread, vol. 1, no. 2, pp. 277–289 (2016). arXiv preprint arXiv:1603.05794
- 33.Osemwinyen AC, Diakhaby A. Mathematical modelling of the transmission dynamics of ebola virus. Appl. Comput. Math. 2015;4(4):313–320. doi: 10.11648/j.acm.20150404.19. [DOI] [Google Scholar]