Skip to main content
Springer Nature Link
Log in

The impact of information and saturated treatment with time delay in an infectious disease model

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

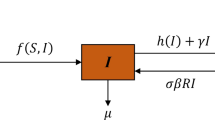
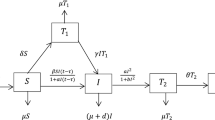
In this paper, we propose a mathematical model with a saturated treatment rate in the presence of information. We consider that the information about the disease affects the transmission rate of infection and hence the transmission rate is corrected. We also assume that people are losing their immunity against disease and the model is of SIRS type. We analyse the stability of the model system and our analysis shows that the model possesses the existence of backward bifurcation and multiple endemic steady states. The saturation in treatment is an important factor causing backward bifurcation. Various situations of multiple endemic steady states are explored numerically. We observe that our model shows existence of bi-stability via backward bifurcation, oscillations and hysteresis. Further, we extend the model to include the time lag in information and we find that in presence of time delay, the endemic steady state destabilizes and oscillations are observed. Thus, we conclude that if information dissemination is delayed beyond a threshold time then the infection oscillates in population and it may lead to difficulty in controlling the disease. Also, nonlinear incidence rate and saturated treatment may cause the existence of multiple endemic steady states and hence leads to complex dynamics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Armbruster, B., Brandeau, M.L.: Cost-effective control of chronic viral diseases: finding the optimal level of screening and contact tracing. Math. Biosci. 224(1), 35–42 (2010)

    MathSciNet  MATH  Google Scholar 

  2. Blower, S.M., Dowlatabadi, H.: Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example. Int. Stat. Rev./Rev. Int. Stat. 62, 229–243 (1994)

    MATH  Google Scholar 

  3. Castilho, C.: Optimal control of an epidemic through educational campaigns. Electron. J. Differ. Equ. 2006(125), 1–11 (2006)

    MathSciNet  MATH  Google Scholar 

  4. Castillo-Chavez, C., Feng, Zn, Huang, W.: On the computation of $r_0$ and its role on. Math. Approach. Emerg. Reemerg. Infect. Dis. Introd. 1, 229 (2002)

    MathSciNet  MATH  Google Scholar 

  5. Castillo-Chavez, C., Song, B.: Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 1(2), 361–404 (2004)

    MathSciNet  MATH  Google Scholar 

  6. Choi, S., Jung, E.: Optimal tuberculosis prevention and control strategy from a mathematical model based on real data. Bull. Math. Biol. 76, 1566–1589 (2014)

    MathSciNet  MATH  Google Scholar 

  7. Collinson, S., Heffernan, J.M.: Modelling the effects of media during an influenza epidemic. BMC Public Health 14, 376 (2014)

    Google Scholar 

  8. Cui, J., Mu, X., Wan, H.: Saturation recovery leads to multiple endemic equilibria and backward bifurcation. J. Theor. Biol. 254(2), 275–283 (2008)

    MathSciNet  MATH  Google Scholar 

  9. Cui, J., Sun, Y., Zhu, H.: The impact of media on the control of infectious diseases. J. Dyn. Differ. Equ. 20(1), 31–53 (2008)

    MathSciNet  MATH  Google Scholar 

  10. d’Onofrio, A., Manfredi, P., Salinelli, E.: Vaccinating behaviour, information, and the dynamics of SIR vaccine preventable diseases. Theor. Popul. Biol. 71(3), 301–317 (2007)

    MATH  Google Scholar 

  11. Dubey, B., Patra, A., Srivastava, P.K., Dubey, U.S.: Modeling and analysis of an SEIR model with different types of nonlinear treatment rates. J. Biol. Syst. 21(03), 1350023 (2013)

    MathSciNet  MATH  Google Scholar 

  12. Greenhalgh, D., Rana, S., Samanta, S., Sardar, T., Bhattacharya, S., Chattopadhyay, J.: Awareness programs control infectious disease-multiple delay induced mathematical model. Appl. Math. Comput. 251, 539–563 (2015)

    MathSciNet  MATH  Google Scholar 

  13. Hu, Z., Liu, S., Wang, H.: Backward bifurcation of an epidemic model with standard incidence rate and treatment rate. Nonlinear Anal. Real World Appl. 9(5), 2302–2312 (2008)

    MathSciNet  MATH  Google Scholar 

  14. Hu, Z., Ma, W., Ruan, S.: Analysis of SIR epidemic models with nonlinear incidence rate and treatment. Math. Biosci. 238(1), 12–20 (2012)

    MathSciNet  MATH  Google Scholar 

  15. Joshi, H.R., Lenhart, S., Hota, S., Augusto, F.B.: Optimal control of an SIR model with changing behavior through an education campaign. Electron. J. Differ. Equ. 2015(50), 1–14 (2015)

    MathSciNet  MATH  Google Scholar 

  16. Kassa, S.M., Ouhinou, A.: Epidemiological models with prevalence dependent endogenous self-protection measure. Math. Biosci. 229(1), 41–49 (2011)

    MathSciNet  MATH  Google Scholar 

  17. Kiss, I.Z., Cassell, J., Recker, M., Simon, P.L.: The impact of information transmission on epidemic outbreaks. Math. Biosci. 225(1), 1–10 (2010)

    MathSciNet  MATH  Google Scholar 

  18. Kumar, A., Srivastava, P.K.: Vaccination and treatment as control interventions in an infectious disease model with their cost optimization. Commun. Nonlinear Sci. Numer. Simul. 44, 334–343 (2017)

    MathSciNet  MATH  Google Scholar 

  19. LaSalle, J.P.: The Stability of Dynamical Systems. Regional Conference Series in Applied Mathematics. SIAM, Philadelphia (1976)

    MATH  Google Scholar 

  20. Lee, S., Chowell, G., Castillo-Chávez, C.: Optimal control for pandemic influenza: the role of limited antiviral treatment and isolation. J. Theor. Biol. 265(2), 136–150 (2010)

    MathSciNet  MATH  Google Scholar 

  21. Li, X.Z., Li, W.S., Ghosh, M.: Stability and bifurcation of an SIS epidemic model with treatment. Chaos Solitons Fractals 42(5), 2822–2832 (2009)

    MathSciNet  MATH  Google Scholar 

  22. Li, X.Z., Li, W.S., Ghosh, M.: Stability and bifurcation of an SIR epidemic model with nonlinear incidence and treatment. Appl. Math. Comput. 210(1), 141–150 (2009)

    MathSciNet  MATH  Google Scholar 

  23. Liu, R., Wu, J., Zhu, H.: Media/psychological impact on multiple outbreaks of emerging infectious diseases. Comput. Math. Methods Med. 8(3), 153–164 (2007)

    MathSciNet  MATH  Google Scholar 

  24. Liu, X., Takeuchi, Y., Iwami, S.: SVIR epidemic models with vaccination strategies. J. Theor. Biol. 253(1), 1–11 (2008)

    MathSciNet  MATH  Google Scholar 

  25. Liu, Y., Cui, J.: The impact of media coverage on the dynamics of infectious disease. Int. J. Biomath. 1(1), 65–74 (2008)

    MathSciNet  MATH  Google Scholar 

  26. Misra, A.K., Sharma, A., Shukla, J.B.: Modeling and analysis of effects of awareness programs by media on the spread of infectious diseases. Math. Comput. Model. 53(5), 1221–1228 (2011)

    MathSciNet  MATH  Google Scholar 

  27. Okosun, K.O., Makinde, O.D., Takaidza, I.: Impact of optimal control on the treatment of HIV/AIDS and screening of unaware infectives. Appl. Math. Model. 37(6), 3802–3820 (2013)

    MathSciNet  MATH  Google Scholar 

  28. Rahman, M.S., Rahman, M.L.: Media and education play a tremendous role in mounting AIDS awareness among married couples in bangladesh. AIDS Res. Therapy 4(1), 10 (2007)

    Google Scholar 

  29. Song, B., Du, W., Lou, J.: Different types of backward bifurcations due to density-dependent treatments. Math. Biosci. Eng. 10(5–6), 1651 (2013)

    MathSciNet  MATH  Google Scholar 

  30. Tchuenche, J.M., Bauch, C.T.: Dynamics of an infectious disease where media coverage influences transmission. ISRN Biomath. 2012, 581274 (2012)

    MATH  Google Scholar 

  31. Tchuenche, J.M., Dube, N., Bhunu, C.P., Smith, R.J., Bauch, C.T.: The impact of media coverage on the transmission dynamics of human influenza. BMC Public Health 11(1), S5 (2011)

    Google Scholar 

  32. Van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1), 29–48 (2002)

    MathSciNet  MATH  Google Scholar 

  33. Verelst, F., Willem, L., Beutels, P.: Behavioural change models for infectious disease transmission: a systematic review (2010–2015). J. R. Soc. Interface 13(125), 20160820 (2016)

    Google Scholar 

  34. Wang, J., Liu, S., Zheng, B., Takeuchi, Y.: Qualitative and bifurcation analysis using an SIR model with a saturated treatment function. Math. Comput. Model. 55(3), 710–722 (2012)

    MathSciNet  MATH  Google Scholar 

  35. Wang, W.: Backward bifurcation of an epidemic model with treatment. Math. Biosci. 201(1), 58–71 (2006)

    MathSciNet  MATH  Google Scholar 

  36. Wang, W., Ruan, S.: Bifurcations in an epidemic model with constant removal rate of the infectives. J. Math. Anal. Appl. 291(2), 775–793 (2004)

    MathSciNet  MATH  Google Scholar 

  37. Wangari, Isaac Mwangi, Stone, Lewi: Backward bifurcation and hysteresis in models of recurrent tuberculosis. PLoS One 13(3), e0194256 (2018)

    Google Scholar 

  38. Wangari, Isaac Mwangi, Trauer, James, Stone, Lewi: Modelling heterogeneity in host susceptibility to tuberculosis and its effect on public health interventions. PLoS One 13(11), e0206603 (2018)

    Google Scholar 

  39. Wei, J., Cui, J.A.: Dynamics of SIS epidemic model with the standard incidence rate and saturated treatment function. Int. J. Biomath. 5(03), 1260003 (2012)

    MathSciNet  MATH  Google Scholar 

  40. WHO: The top 10 causes of death. http://www.who.int/mediacentre/factsheets/fs310/en/

  41. Whyte, S., Harnan, S.: Effectiveness and cost-effectiveness of an awareness campaign for colorectal cancer: a mathematical modeling study. Cancer Causes Control 25(6), 647–658 (2014)

    Google Scholar 

  42. Zhang, X., Liu, X.: Backward bifurcation of an epidemic model with saturated treatment function. J. Math. Anal. Appl. 348(1), 433–443 (2008)

    MathSciNet  MATH  Google Scholar 

  43. Zhang, X., Liu, X.: Backward bifurcation and global dynamics of an SIS epidemic model with general incidence rate and treatment. Nonlinear Anal. Real World Appl. 10(2), 565–575 (2009)

    MathSciNet  MATH  Google Scholar 

  44. Zhao, H., Lin, Y., Dai, Y.: An SIRS epidemic model incorporating media coverage with time delay. Comput. Math. Methods Med. 2014, 680743 (2014)

    MathSciNet  MATH  Google Scholar 

  45. Zhonghua, Z., Yaohong, S.: Qualitative analysis of a SIR epidemic model with saturated treatment rate. J. Appl. Math. Comput. 34(1), 177–194 (2010)

    MathSciNet  MATH  Google Scholar 

  46. Zhou, L., Fan, M.: Dynamics of an SIR epidemic model with limited medical resources revisited. Nonlinear Anal. Real World Appl. 13(1), 312–324 (2012)

    MathSciNet  MATH  Google Scholar 

  47. Zhou, T., Zhang, W., Lu, Q.: Bifurcation analysis of an SIS epidemic model with saturated incidence rate and saturated treatment function. Appl. Math. Comput. 226, 288–305 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

PKS acknowledges the financial support from SERB (DST) ProjectNoMTR/2017/000803. The authors thank anonymous referees and handling editor for their inputs that has improved manuscript significantly.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Patna, Patna, 801 103, India

    Anuradha Yadav & Prashant K. Srivastava

Authors
  1. Anuradha Yadav
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Prashant K. Srivastava
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Prashant K. Srivastava.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yadav, A., Srivastava, P.K. The impact of information and saturated treatment with time delay in an infectious disease model. J. Appl. Math. Comput. 66, 277–305 (2021). https://doi.org/10.1007/s12190-020-01436-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01436-2

Keywords