Skip to main content
Springer Nature Link
Log in

Numerical solution of a fractional-order Bagley–Torvik equation by quadratic finite element method

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

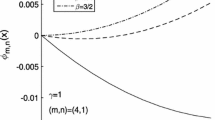
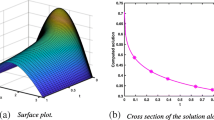
Abstract

The fractional-order Bagley–Torvik equation has many applications in the field of life science and engineering. In this paper, we develop a new scheme based on the existing finite element method for the numerical solution of the Bagley–Torvik equation of order (0, 2). We adopt the formulation of the equation in a simple and generalized way. The existence and uniqueness of the solution and its error estimations are derived based on the technique we derived. A series of numerical examples are provided to demonstrate the accuracy, efficiency, and simplicity of the method. The results are depicted graphically and in a table to compare the exact and approximate solutions obtained by following the numerical methods available in the literature. The numerical experiment shows that using a small number of quadratic functions, the accuracy of our numerical technique is better than the existing methods. Since the Bagley–Torvik equation represents the general form of fractional-order boundary value problems, the numerical technique indicates the identical path to solve the similar type of the fractional-order boundary value problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Kulish, V.V., Lage, J.L.: Application of fractional calculus to fluid mechanics. J. Fluids Eng. 124(3), 803–806 (2002)

    Article  Google Scholar 

  2. Lederman, C., Roquejoffre, J.M., Wolanski, N.: Mathematical justification of a nonlinear integro-differential equation for the propagation of spherical flames. Annali di Matematica Pura ed Applicata 183(2), 173–239 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  3. Duarte, F.B., Machado, J.T.: Chaotic phenomena and fractional-order dynamics in the trajectory control of redundant manipulators. Nonlinear Dyn. 29(1–4), 315–342 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bagley, R.L., Torvik, P.J.: Fractional calculus-a different approach to the analysis of viscoelastically damped structures. AIAA J. 21(5), 741–748 (1983)

    Article  MATH  Google Scholar 

  5. Torvik, P.J., Bagley, R.L.: On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 51(2), 294–298 (1984)

    Article  MATH  Google Scholar 

  6. Engheta, N.: On fractional calculus and fractional multipoles in electromagnetism. IEEE Trans. Antennas Propag. 44(4), 554–566 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  7. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Elsevier, Amsterdam (1998)

    MATH  Google Scholar 

  8. Ray, S.S.: On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley Torvik equation. Appl. Math. Comput. 218(9), 5239–5248 (2012)

    MathSciNet  MATH  Google Scholar 

  9. Saw, V., Kumar, S.: Numerical solution of fraction Bagley–Torvik boundary value problem based on chebyshev collocation method. Int. J. Appl. Comput. Math. 5(3), 68 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  10. Bagley, R.L., Torvik, P.J.: Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 23(6), 918–925 (1985)

    Article  MATH  Google Scholar 

  11. Shen, S.J., Liu, F.W.: A computationally effective numerical method for the fractional-order Bagley–Torvik equation. J.-Xiamen Univ. Nat. Sci. 43(3), 311–315 (2004)

    MathSciNet  MATH  Google Scholar 

  12. Wang, Z.H., Wang, X.: General solution of the Bagley–Torvik equation with fractional-order derivative. Commun. Nonlinear Sci. Numer. Simul. 15(5), 1279–1285 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  13. Staněk, S.: The Neumann problem for the generalized Bagley–Torvik fractional differential equation. Fract. Calc. Appl. Anal. 19(4), 907 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Diethelm, K.: The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type. Springer, Berlin (2010)

    Book  MATH  Google Scholar 

  15. Fitt, A.D., Goodwin, A.R.H., Ronaldson, K.A., Wakeham, W.A.: A fractional differential equation for a MEMS viscometer used in the oil industry. J. Comput. Appl. Math. 229(2), 373–381 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Zolfaghari, M., Ghaderi, R., SheikholEslami, A., Ranjbar, A., Hosseinnia, S.H., Momani, S., Sadati, J.: Application of the enhanced homotopy perturbation method to solve the fractional-order Bagley–Torvik differential equation. Phys. Scr. 136, 014032 (2009)

    Article  Google Scholar 

  17. Mekkaoui, T., Hammouch, Z.: Approximate analytical solutions to the Bagley–Torvik equation by the fractional iteration method. Ann. Univ. Craiova-Math. Comput. Sci. Ser. 39(2), 251–256 (2012)

    MathSciNet  MATH  Google Scholar 

  18. Ray, S.S., Bera, R.K.: Analytical solution of the Bagley Torvik equation by Adomian decomposition method. Appl. Math. Comput. 168(1), 398–410 (2005)

    MathSciNet  MATH  Google Scholar 

  19. ur Rehman, M., & Khan, R. A., : A numerical method for solving boundary value problems for fractional differential equations. Appl. Math. Model. 36(3), 894–907 (2012)

  20. Mashayekhi, S., Razzaghi, M.: Numerical solution of the fractional Bagley–Torvik equation by using hybrid functions approximation. Math. Methods Appl. Sci. 39(3), 353–365 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Diethelm, K., Ford, J.: Numerical solution of the Bagley–Torvik equation. BIT Numer. Math. 42(3), 490–507 (2002)

    MathSciNet  MATH  Google Scholar 

  22. Çenesiz, Y., Keskin, Y., Kurnaz, A.: The solution of the Bagley–Torvik equation with the generalized Taylor collocation method. J. Frankl. Inst. 347(2), 452–466 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mokhtary, P.: Numerical treatment of a well-posed Chebyshev Tau method for Bagley–Torvik equation with high-order of accuracy. Numer. Algorithms 72(4), 875–891 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Ding, Q., Wong, P.J.: Numerical method for fractional Bagley–Torvik equation. In: AIP Conference Proceedings, AIP Publishing LLC. 2116(1), 240007 (2019)

  25. Yüzbaşi, Ş.: Numerical solution of the Bagley–Torvik equation by the Bessel collocation method. Math. Methods Appl. Sci. 36(3), 300–312 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  26. Karaaslan, M.F., Celiker, F., Kurulay, M.: Approximate solution of the Bagley–Torvik equation by hybridizable discontinuous Galerkin methods. Appl. Math. Comput. 285, 51–58 (2016)

    MathSciNet  MATH  Google Scholar 

  27. Krishnasamy, V.S., Razzaghi, M.: The numerical solution of the Bagley-Torvik equation with fractional Taylor method. J. Comput. Nonlinear Dyn. 11(5), 1–6 (2016)

    Google Scholar 

  28. Raja, M.A.Z., Samar, R., Manzar, M.A., Shah, S.M.: Design of unsupervised fractional neural network model optimized with interior point algorithm for solving Bagley–Torvik equation. Math. Comput. Simul. 132, 139–158 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  29. Raja, M.A.Z., Khan, J.A., Qureshi, I.M.: Solution of fractional order system of Bagley-Torvik equation using evolutionary computational intelligence. Math. Probl. Eng. 675075 (2011). https://doi.org/10.1155/2011/675075

  30. Zahra, W.K., Elkholy, S.M.: Quadratic spline solution for boundary value problem of fractional order. Numer. Algorithms 59(3), 373–391 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  31. Zahra, W K., Elkholy, S.M.: The use of cubic splines in the numerical solution of fractional differential equations. Int. J. Math. Math. Sci. 638026 (2012). https://doi.org/10.1155/2012/638026

  32. Zahra, W.K., Elkholy, S.M.: Cubic spline solution of fractional Bagley–Torvik equation. Electron. J. Math. Anal. Appl. 1(2), 230–241 (2013)

    MATH  Google Scholar 

  33. Zahra, W.K., Van Daele, M.: Discrete spline methods for solving two point fractional Bagley–Torvik equation. Appl. Math. Comput. 296, 42–56 (2017)

    MathSciNet  MATH  Google Scholar 

  34. Wang, H., Yang, D., Zhu, S.: A Petrov–Galerkin finite element method for variable-coefficient fractional diffusion equations. Comput. Methods Appl. Mech. Eng. 290, 45–56 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  35. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)

    Book  MATH  Google Scholar 

  36. Sebah, P., Gourdon, X.: Introduction to the gamma function. 1–20 (2002). https://www.csie.ntu.edu.tw/~b89089/link/gammaFunction.pdf

  37. Ding, Q.: Numerical treatment of certain fractional and non-fractional differential equations. Doctoral thesis, Nanyang Technological University, Singapore (2020)

  38. Ali, H., Islam, M.S.: Generalized Galerkin finite element formulation for the numerical solutions of second order nonlinear boundary value problems. GANIT J. Bangladesh Math. Soc. 37, 147–159 (2017)

    Article  MathSciNet  Google Scholar 

  39. Ervin, V.J., Roop, J.P.: Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ. Int. J. 22(3), 558–576 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  40. Hao, Z., Park, M., Lin, G., Cai, Z.: Finite element method for two-sided fractional differential equations with variable coefficients: Galerkin approach. J. Sci. Comput. 79(2), 700–717 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  41. Brenner, S., Scott, R.: The Mathematical Theory of Finite Element Methods, vol. 15. Springer, Berlin (2007)

    Google Scholar 

Download references

Acknowledgements

The authors are grateful to the reviewers for their constructive suggestions to develop the quality of the manuscript significantly. The author M. Kamrujjaman research was partially supported by the University Grant Commission (UGC), for year 2019-2020, Bangladesh.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, University of Dhaka, Dhaka, 1000, Bangladesh

    Hazrat Ali

  2. Department of Mathematics, University of Dhaka, Dhaka, 1000, Bangladesh

    Md. Kamrujjaman

  3. Department of Mathematics and Statistics, University of Calgary, Calgary, AB, Canada

    Md. Kamrujjaman

  4. Department of Electrical and Computer Engineering, University of New Mexico, Albuquerque, USA

    Afroza Shirin

Authors
  1. Hazrat Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Md. Kamrujjaman
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Afroza Shirin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Md. Kamrujjaman.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, H., Kamrujjaman, M. & Shirin, A. Numerical solution of a fractional-order Bagley–Torvik equation by quadratic finite element method. J. Appl. Math. Comput. 66, 351–367 (2021). https://doi.org/10.1007/s12190-020-01440-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01440-6

Keywords

Mathematics Subject Classification