Skip to main content

Advertisement

Springer Nature Link
Log in

Approximate solution of singular IVPs of Lane–Emden type and error estimation via advanced Adomian decomposition method

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

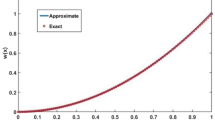
This article aims to present a simple and effective method, named as advanced Adomian decomposition method, to attain the approximate solution of singular initial value problems of Lane–Emden type. Also, convergence analysis and error analysis with an upper bound of the absolute error for the proposed method are discussed. The proposed method is capable to remove the singular behaviour of the problems and provides an approximate solution up to the desired order. To illustrate the reliability and validity of the proposed method with error estimate several examples that arise in applications are considered and the attained outcomes are compared with some existing numerical methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Lane, J.H.: On the theoretical temperature of the sun. Am. J. Sci. Arts 50, 57–74 (1870)

    Article  Google Scholar 

  2. Emden, R.: Gaskugein: Anwendugen der mechanischen warmetheoric. B.G, Tewbner, Leipzig and Berlin (1907)

  3. Davis, H.T.: Introduction to Non-linear Differential and Integral Equations. Dover, New York (1962)

    Google Scholar 

  4. Chandrasekhar, S.: Introduction to Study of Stellar Structure. Dover, New York (1967)

    Google Scholar 

  5. Richardson, O.U.: The emission of electricity from hot bodies. Longman, Green and Co., London (1921)

    Google Scholar 

  6. Chowdhury, M.S.H., Hashim, I.: Solutions of a class of singular second-order IVPs by homotopy-perturbation method. Phys. Lett. A 365, 439–447 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Horedt, G.P.: Exact solutions of the Lane–Emden equation in N-dimensional space. Astron. Astrophys. 160, 148–156 (1986)

    MATH  Google Scholar 

  8. Horedt, G.P.: Approximate analytical solutions of the Lane–Emden equation in N-dimensional space. Astron. Astrophys. 172, 359–367 (1987)

    MathSciNet  MATH  Google Scholar 

  9. Umesh, Kumar, M.: Numerical solution of Lane-Emden type equations using Adomian decomposition method with unequal step-size partitions. Eng. Comput. (2020). https://doi.org/10.1108/EC-02-2020-0073

  10. Alzate, P.P.C., Urueña, W.A.: The Zhou’s method for solving the White-Dwarfs equation. Appl. Math. 4, 28–32 (2013)

    Article  Google Scholar 

  11. Khalique, C.M., Ntsime, P.: Exact solutions of the Lane–Emden type equations. New Astron. 13(7), 476–480 (2008)

    Article  Google Scholar 

  12. Aminikhah, H., Moradian, S.: Numerical solution of singular Lane–Emden equation. ISRN Math. Phys. 2013, 1–9 (2013)

    Article  MATH  Google Scholar 

  13. Khan, Y., Svoboda, Z., Smarda, Z.: Solving certain classes of Lane–Emden type equations using the differential transformation method. Adv. Differ. Equ. 174, 1–11 (2012)

    MathSciNet  MATH  Google Scholar 

  14. Yigider, M., Tabatabaei, K., Celik, E.: The numerical method for solving differential equations of Lane–Emden type by Pad’e approximation. Discrete Dyn. Nat. Soc. 2011, 1–9 (2011)

    Article  MATH  Google Scholar 

  15. Bhrawy, A.H., Alofi, A.S.: A Jacobi-Gauss collocation method for solving nonlinear Lane-Emden type equations. Commun. Nonlinear Sci. Numer. Simul. 17, 62–70 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  16. Singh, H.: An efficient computational method for the approximate solution of nonlinear Lane–Emden type equations arising in astrophysics. Astrophys. Space Sci. 363(4), 1–10 (2018)

    Article  MathSciNet  Google Scholar 

  17. Yin, F.K., Han, W.Y., Song, J.Q.: Modified Laplace decomposition method for Lane-Emden type differential equations. Int. J. Appl. Phys. Math. 3(2), 98–102 (2013)

    Article  Google Scholar 

  18. Chowdhury, M.S.H., Hashim, I.: Solutions of Emden-Fowler equations by homotopy-perturbation method. Nonlinear Anal. Real World Appl. 10, 104–115 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Parand, K., Shahini, M., Dehghan, M.: Rational Legendre pseudospectral approach for solving non-linear differential equations of Lane–Emden type. J. Comput. Phys. 228, 8830–8840 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Mohanty, R., Ghosh, B.P.: Absolute stability of an implicit method based on third-order off-step discretization for the initial-value problem on a graded mesh. Eng. Comput. (2019). https://doi.org/10.1007/s0036-019-00857-3

  21. Ramos, J.I.: Linearization techniques for singular initial-value problems of ordinary differential equations. Appl. Math. Comput. 161, 525–542 (2005)

    MathSciNet  MATH  Google Scholar 

  22. Mandelzweig, V.B., Tabakin, F.: Quasilinearization approach to nonlinear problems in physics with application to nonlinear ODEs. Comput. Phys. Commun. 141(2), 268–281 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  23. Duan, J.S., Rach, R., Wazwaz, A.M.: Higher-order numeric solutions of the Lane–Emden type equations derived from the multi-stage modified Adomian decomposition method. Int. J. Comput. Math. 94(1), 197–215 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Aminikhah, H.: Solutions of the singular IVPs of Lane–Emden type equations by combining Laplace transformation and perturbation technique. Nonlinear Eng. 7(4), 273–278 (2018)

    Article  MathSciNet  Google Scholar 

  25. Bender, C.M., Milton, K.A., Pinsky, S.S., Simmons, J.L.M.: A new perturbative approach to non linear problems. J. Math. Phys. 30(7), 1447–1455 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  26. Rach, R., Adomian, G., Meyers, R.E.: A modified decomposition. Comput. Math. Appl. 23(1), 17–23 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  27. Adomian, G., Rach, R.: Nonlinear transformation of series-part II. Comput. Math. Appl. 23(10), 79–83 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  28. Duan, J.S.: Convenient analytic recurrence algorithms for the Adomian polynomials. Appl. Math. Comput. 217, 6337–6348 (2011)

    MathSciNet  MATH  Google Scholar 

  29. Rach, R.: A convenient computational form for the Adomian polynomials. J. Math. Anal. Appl. 102, 415–419 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  30. Kaliyappan, M., Hariharan, S.: Symbolic computation of Adomian polynomials based on Rach’s rule. Br. J. Math. Comput. Sci. 5(5), 562–570 (2015)

    Article  Google Scholar 

  31. Liu, J.G., Yang, X.J., Feng, Y.Y.: On integrability of the time fractional nonlinear heat conduction equation. J. Geom. Phys. 144, 190–198 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  32. Al-sawalha, M.M.: Synchronization of different order fractional-order chaotic systems using modify adaptive sliding mode control. Adv. Differ. Equ. (2019). https://doi.org/10.1186/s1362-020-0287-7

  33. Liu, J.G., Yang, X.J., Feng, Y.Y., Cui, P.: On group analysis of the time fractional extended (2+1)-dimensional Zakharov-Kuznetsov equation in quantum magneto-plasmas. Math. Comput. Simul. 178, 407–421 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Feng, Y.Y., Yang, X.J., Liu, J.G.: On overall behavior of Maxwell mechanical model by the combined Caputo fractional derivative. Chin. J. Phys. 66, 269–276 (2020)

    Article  MathSciNet  Google Scholar 

  35. Cherruault, Y., Adomian, G.: Decomposition methods: a new proof of convergence. Comput. Math. Appl. 18(12), 103–106 (1993)

    MathSciNet  MATH  Google Scholar 

  36. Abdelrazec, A., Pelinovsky, D.: Convergence of the Adomian decomposition method for initial-value problems. Numer. Methods Partial Differ. Equ. 27(4), 749–766 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  37. Umesh, Kumar,M.:Numerical solution of singular boundary value problems using advanced Adomian decomposition method. Eng. Comput. (2020). https://doi.org/10.1007/s0036-020-00972-6

  38. Ray, S.S.: New approach for general convergence of the Adomian decomposition method. World Appl. Sci. J. 32(11), 2264–2268 (2014)

    Google Scholar 

  39. Cooper, G.J.: Error bounds for numerical solutions of ordinary differential equation. Numer. Math. 18, 162–170 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  40. Warne, P.G., Polignone, W.D.A., Sochacki, J.S., Parker, G.E., Carothers, D.C.: Explicit A—priori error bounds and Adaptive error control for approximation of non-linear initial value differential systems. Comput. Math. Appl. 52, 1695–1710 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  41. Yuzbasi, S.: A numerical approach for solving a class of the nonlinear Lane–Emden type equations arising in astrophysics. Math. Methods Appl. Sci. 34, 2218–2230 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  42. Wazwaz, A.M.: A new algorithm for solving differential equations of Lane–Emden type. Appl. Math. Comput. 118, 287–310 (2001)

    MathSciNet  MATH  Google Scholar 

  43. Doha, E.H., Bhrawy, A.H., Hafez, R.M., Gorder, R.A.: A Jacobi rational pseudospectral method for Lane–Emden initial value problems arising in astrophysics on a semi-infinite interval. Comput. Appl. Math. 33, 607–619 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  44. Mall, S., Chakraverty, S.: Chebyshev neural network based model for solving Lane–Emden type equations. Appl. Math. Comput. 247, 100–114 (2014)

    MathSciNet  MATH  Google Scholar 

  45. Pandey, R.K., Kumar, N.: Solution of Lane–Emden type equations using Bernstein operational matrix of differentiation. New Astron. 17(3), 303–308 (2012)

    Article  Google Scholar 

Download references

Acknowledgements

We express our sincere thanks to the editor in chief, editor and reviewers for their valuable suggestions to revise this manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics, Motilal Nehru National Institute of Technology Allahabad, Prayagraj, U.P, 211004, India

    Umesh & Manoj Kumar

Authors
  1. Umesh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Manoj Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Umesh.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Umesh, Kumar, M. Approximate solution of singular IVPs of Lane–Emden type and error estimation via advanced Adomian decomposition method. J. Appl. Math. Comput. 66, 527–542 (2021). https://doi.org/10.1007/s12190-020-01444-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01444-2

Keywords

Mathematics Subject Classification