Abstract
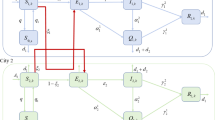
Human mobility has been significantly influencing public health since time immemorial. A susceptible-infected-deceased epidemic reaction diffusion network model using asymptotic transmission rate is proposed to portray the spatial spread of the epidemic among two cities due to population dispersion. Qualitative behaviour including global attractor and persistence property are obtained. We also study asymptotic behaviour of the whole network with the help of asymptotic behaviour at individual cities. The epidemic model shows up two equilibria, (i) the disease-free, and (ii) unique endemic equilibria. An expression that can be used to calculate the basic reproduction number for heterogeneous environment, for the entire network is obtained. We use graph theory to analyze the global stability of our diffusive two-city model. We also performed bifurcation analysis and discovered that endemic equilibrium changes stability via Hopf bifurcations. A significant reduction in the number of infectives were observed when proper migration rate is maintained between the cities. Numerical results are provided to illuminate and clarify theoretical findings. Simulation experiments for two-dimensional spatial models show that infectious populations will increase if contact heterogeneity is increased, but it will decline if infective populations perform more local random movement. We observe that infection risk may be understated if the parameters used to estimate the basic reproduction number remains unchanged through space or time.









Similar content being viewed by others
References
Allen, L.J., Bolker, B.M., Lou, Y., Nevai, A.L.: Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model. Discrete Contin. Dyn. Syst. 21(1), 1 (2008)
Anderson, R.M., May, R.: Infectious Diseases of Humans. Oxford Science Publication Google Scholar, New York (1991)
Arino, J., Van den Driessche, P.: A multi-city epidemic model. Math. Popul. Stud. 10(3), 175–193 (2003)
Berman, A., Plemmons, R.J.: Nonnegative Matrices in the Mathematical Sciences, vol. 9. SIAM, Philadelphia (1994)
Brézis, H., Strauss, W.A.: Semi-linear second-order elliptic equations in L1. J. Math. Soc. Jpn. 25(4), 565–590 (1973)
Brockmann, D., Hufnagel, L., Geisel, T.: The scaling laws of human travel. Nature 439(7075), 462 (2006)
Chen, W., Wang, M.: Qualitative analysis of predator-prey models with Beddington-Deangelis functional response and diffusion. Math. Comput. Modell. 42(1–2), 31–44 (2005)
Cui, R., Lou, Y.: A spatial sis model in advective heterogeneous environments. J. Differ. Equ. 261(6), 3305–3343 (2016)
Deng, K., Wu, Y.: Dynamics of a susceptible-infected-susceptible epidemic reaction-diffusion model. Proc. Sect. A Math. R. Soc. Edinb. 146(5), 929 (2016)
Diekmann, O., Kretzschmar, M.: Patterns in the effects of infectious diseases on population growth. J. Math. Biol. 29(6), 539–570 (1991)
Fife, P.C.: Mathematical Aspects of Reacting and Diffusing Systems, vol. 28. Springer, Berlin (2013)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2015)
Guin, L.N., Mandal, P.K.: Spatiotemporal dynamics of reaction-diffusion models of interacting populations. Appl. Math. Model. 38(17–18), 4417–4427 (2014)
Hethcote, H.W.: Qualitative analyses of communicable disease models. Math. Biosci. 28(3–4), 335–356 (1976)
Hethcote, H.W.: The mathematics of infectious diseases. SIAM Rev. 42(4), 599–653 (2000)
Huang, W., Han, M., Liu, K.: Dynamics of an sis reaction-diffusion epidemic model for disease transmission. Math. Biosci. Eng. 7(1), 51 (2010)
Jorgensen, S.E.: Handbook of Environmental Data and Ecological Parameters, vol. 6. Pergamon, Bergama (1979)
Keeling, M., Rohani, P.: Modeling infectious diseases in humans and animals. Clin. Infect. Dis. 47, 864–6 (2008)
Knuth, D.E.: The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1. Pearson Education, Chennai (2011)
Krein, M.G.: Linear operators leaving invariant a cone in a Banach space. Am. Math. Soc. Transl. Ser. I(10), 199–325 (1962)
Kuto, K., Matsuzawa, H., Peng, R.: Concentration profile of endemic equilibrium of a reaction-diffusion-advection sis epidemic model. Calc. Var. Partial. Differ. Equ. 56(4), 112 (2017)
Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory, vol. 112. Springer, Berlin (2013)
Lam, K.Y., Lou, Y.: Asymptotic behavior of the principal eigenvalue for cooperative elliptic systems and applications. J. Dyn. Differ. Equ. 28(1), 29–48 (2016)
LaSalle, J.P.: The Stability of Dynamical Systems, vol. 25. SIAM, Philadelphia (1976)
Lei, C., Li, F., Liu, J.: Theoretical analysis on a diffusive sir epidemic model with nonlinear incidence in a heterogeneous environment. Discrete Contin. Dyn. Syst.-B 23(10), 4499 (2018)
Lei, C., Xiong, J., Zhou, X.: Qualitative Analysis on an SIS epidemic reaction-diffusion model with mass action infection mechanism and spontaneous infection in a heterogeneous environment. Discrete Contin. Dyn. Syst.-B 22(11), 1 (2019)
Li, B., Bie, Q.: Long-time dynamics of an sirs reaction-diffusion epidemic model. J. Math. Anal. Appl. 475(2), 1910–1926 (2019)
Li, M.Y., Shuai, Z.: Global-stability problem for coupled systems of differential equations on networks. J. Differ. Equ. 248(1), 1–20 (2010)
Li, B., Li, H., Tong, Y.: Analysis on a diffusive sis epidemic model with logistic source. Zeitschrift für angewandte Mathematik und Physik 68(4), 96 (2017)
Li, H., Peng, R., Wang, F.B.: Varying total population enhances disease persistence: qualitative analysis on a diffusive sis epidemic model. J. Differ. Equ. 262(2), 885–913 (2017)
Li, H., Peng, R., Wang, Z.A.: On a diffusive susceptible-infected-susceptible epidemic model with mass action mechanism and birth-death effect: analysis, simulations, and comparison with other mechanisms. SIAM J. Appl. Math. 78(4), 2129–2153 (2018)
Lieberman, G.M.: Bounds for the steady-state sel’kov model for arbitrary p in any number of dimensions. SIAM J. Math. Anal. 36(5), 1400–1406 (2005)
Liu, Z., Wang, X., Wang, M.: Inhomogeneity of epidemic spreading. Chaos Interdiscip. J. Nonlinear Sci. 20(2), 023128 (2010)
Lou, Y., Ni, W.M.: Diffusion, self-diffusion and cross-diffusion. J. Differ. Equ. 131(1), 79–131 (1996)
Magal, P., Webb, G., Wu, Y.: On a vector-host epidemic model with spatial structure. Nonlinearity 31(12), 5589 (2018)
Magal, P., Webb, G.F., Wu, Y.: On the basic reproduction number of reaction-diffusion epidemic models. SIAM J. Appl. Math. 79(1), 284–304 (2019)
May, R.M.: Uses and abuses of mathematics in biology. Science 303(5659), 790–793 (2004)
McCallum, H., Barlow, N., Hone, J.: How should pathogen transmission be modelled? Trends Ecol. Evol. 16(6), 295–300 (2001)
Murray, JD.: Mathematical biology II: spatial models and biomedical applications, 3,(2001) Springer-Verlag
Nian, F., Wang, X.: Efficient immunization strategies on complex networks. J. Theor. Biol. 264(1), 77–83 (2010)
Nian, F., Hu, C., Yao, S., Wang, L., Wang, X.: An immunization based on node activity. Chaos Solitons Fractals 107, 228–233 (2018)
Peng, R.: Asymptotic profiles of the positive steady state for an sis epidemic reaction-diffusion model. Part I. J. Differ. Equ. 247(4), 1096–1119 (2009)
Peng, R., Yi, F.: Asymptotic profile of the positive steady state for an sis epidemic reaction-diffusion model: effects of epidemic risk and population movement. Physica D 259, 8–25 (2013)
Peng, R., Zhao, X.Q.: A reaction-diffusion sis epidemic model in a time-periodic environment. Nonlinearity 25(5), 1451 (2012)
Protter, M.H., Weinberger, H.F.: Maximum Principles in Differential Equations. Springer, Berlin (2012)
Ren, G., Wang, X.: Epidemic spreading in time-varying community networks. Chaos Interdiscip. J. Nonlinear Sci. 24(2), 023116 (2014)
Song, P., Lou, Y., Xiao, Y.: A spatial SEIRS reaction-diffusion model in heterogeneous environment. J. Differ. Eq. 267, 5084–5114 (2019)
Strauss, W.A.: Partial Differential Equations: An Introduction. Wiley, Hoboken (2007)
Stürchler, D., et al.: Endemic Areas of Tropical Infections, 2nd edn. Hans Huber Publishers, Saint Paul (1988)
Suo, J., Li, B.: Analysis on a diffusive sis epidemic system with linear source and frequency-dependent incidence function in a heterogeneous environment. Math. Biosci. Eng. 17(1), 418–441 (2020)
Tewa, J.J., Bowong, S., Mewoli, B.: Mathematical analysis of two-patch model for the dynamical transmission of tuberculosis. Appl. Math. Model. 36(6), 2466–2485 (2012)
Thieme, H.R.: Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. SIAM J. Appl. Math. 70(1), 188–211 (2009)
Tong, Y., Lei, C.: An sis epidemic reaction-diffusion model with spontaneous infection in a spatially heterogeneous environment. Nonlinear Anal. Real World Appl. 41, 443–460 (2018)
Upadhyay, R.K., Roy, P., Rai, V.: Deciphering dynamics of epidemic spread: the case of influenza virus. Int. J. Bifurc. Chaos 24(05), 1450064 (2014)
Van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)
Wang, W., Zhao, X.Q.: An epidemic model in a patchy environment. Math. Biosci. 190(1), 97–112 (2004)
Wang, W., Zhao, X.Q.: A nonlocal and time-delayed reaction-diffusion model of dengue transmission. SIAM J. Appl. Math. 71(1), 147–168 (2011)
Wang, W., Zhao, X.Q.: Basic reproduction numbers for reaction-diffusion epidemic models. SIAM J. Appl. Dyn. Syst. 11(4), 1652–1673 (2012)
Wang, X., Zhao, T.: Model for multi-messages spreading over complex networks considering the relationship between messages. Commun. Nonlinear Sci. Numer. Simul. 48, 63–69 (2017)
Wang, X., Zhao, T., Qin, X.: Model of epidemic control based on quarantine and message delivery. Physica A 458, 168–178 (2016)
Wen, X., Ji, J., Li, B.: Asymptotic profiles of the endemic equilibrium to a diffusive sis epidemic model with mass action infection mechanism. J. Math. Anal. Appl. 458(1), 715–729 (2018)
Wen-Jie, Z., Xing-Yuan, W.: Inhomogeneity of epidemic spreading with entropy-based infected clusters. Chaos Interdiscip. J. Nonlinear Sci. 23(4), 043105 (2013)
Wu, Y., Zou, X.: Asymptotic profiles of steady states for a diffusive sis epidemic model with mass action infection mechanism. J. Differ. Equ. 261(8), 4424–4447 (2016)
Xu, Z., Ai, C.: Traveling waves in a diffusive influenza epidemic model with vaccination. Appl. Math. Model. 40(15–16), 7265–7280 (2016)
Acknowledgements
This work is supported by Normandie region France and XTerm ERDF project (European Regional Development Fund) on Complex Network and Applications.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Proposition 5
We consider the following auxiliary system
where \(r_{10}, \beta _{10}, a_{10}\) are positive constant and the parameter \(\theta \in [0,1]\). Problem (74–75) becomes problem (47) at \(\theta =1\). We divide the proof into three parts for easy understanding.
Step 1. We find the upper bounds for any positive solution \((S_1,I_1)\) to (74–75). In view of (74), it holds
Thus, we can find a positive constant C independent of \(\theta \in [0,1]\) such that
and
The positive constant C does not depend on the parameter \(\theta \in [0,1]\) and can be different depending on its position. Applying \(L^1\) estimate theory for elliptic equations [5] to Equ. (74–75), we obtain \(||S_1||_{W^{1,1({\varOmega })}} \le C\) and \(||I_1||_{W^{1,1({\varOmega })}} \le C\). Application of Sobolev embedding theorem gives us,
we have
Applying \(L^p\) estimate for elliptic equations [12] to (74–75) leads to
Again we apply Sobolev embedding theorem, to get
Repeating the above process finitely many times, one can affirm that
Step 2. Now, we find lower bounds for any positive solution \((S_1,I_1)\) to (74–75). Integrating (75) over \({\varOmega }\) gives
Clearly, (81) indicates
where \(c=min(min~~a(x), a_{10})>0, d=max(max ~\beta (x), \beta _{10})>0\). One can then insert \(\int _{\varOmega }I_1 dx \le K_1-\int _{\varOmega }S_1 dx\) into (82) to get
Notice that \(S_1\) satisfies
Thus, together with (83) and Lemma 1 with \(q=1\) concludes that
We next take \(min_{\varOmega }I_1(x)=I(x_0)\). According to [34], one can see
This leads to
If \(\beta _1(x_0) S_1(x_0)/a_1(x_0)-c_1-S_1(x_0)>0\), from the above analysis of step 1 and 2 we can always find a positive constant \(C_*>1\), which is independent of \(\theta \in [0,1]\), such that any positive solution \((S_1,I_1)\) of (74–75) satisfies
Step 3. Finally, we find existence of positive solution to (74–75). Let us denote a set,
Thus, (74–75) has no positive solution \((S_1,I_1)\in \partial {\varTheta }\). For \(\theta \in [0,1],\) we also define the operator
Clearly, the existence of positive solutions of (47) is identical to the existence of fixed point of the operator H(1, .) in \({\varTheta }\). From standard elliptic regularity theory one can find that H is a compact operator from \([0,1] \times {\varTheta }\) to \(C({{\bar{{\varOmega }}}}) \times C({\bar{{\varOmega }}})\). Furthermore, we have
Therefore, the topological degree \(deg(I-H(\theta ,.),{\varTheta })\) is well-defined and is independent of \(\theta \in [0,1]\). Denote
where \(B=(a_1-\beta _1)K_1^2+2K_1(\beta _1(c_1-K_1)+a_1(c_1+K_1))r_1+(c_1+K_1)^2 r_1^2\). [54] have already proved that \((S_{10}^*,I_{10}^*)\) is linearly stable when \(\beta _1(x), r_1(x), a_1(x)\) are constant. Using well-known Leray-Schauder degree index formula, we have
Therefore, from homotopy invariance of the Leray-Schauder degree it follows that
which implies that H(1, .) has at least one fixed point in \({\varTheta }\). As a consequence, (47) has at least one positive solution. \(\square \)
Rights and permissions
About this article
Cite this article
Aziz-Alaoui, M.A., Roy, P. Deciphering role of inter and intracity human dispersal on epidemic spread via coupled reaction-diffusion models. J. Appl. Math. Comput. 66, 769–808 (2021). https://doi.org/10.1007/s12190-020-01450-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-020-01450-4