Skip to main content

Advertisement

SpringerLink
Log in

Optimal control of an online game addiction model with positive and negative media reports

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

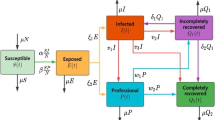
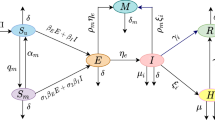
In the spread of infectious diseases, media reports have played a positive role. However, in the process of game communication, there are not only positive but also negative media reports. Therefore, in this paper, we establish a model with positive and negative media reports to analyze the role of media reports in the process of game communication. First, we study its positivity and boundedness, and calculate the basic reproduction number \(R_{0}\) under three different incidence rates. The existence and stability of the equilibria are proved. Secondly, the optimal control problem is studied by adding two dynamic variables of media reports. Finally, in the simulation we simulate the stability of the equilibria, so as to verify the correctness of the theory. Then the influence of media parameters on \(R_{0}\) is analyzed. The numerical results of optimal control are simulated by forward and backward sweep method. By comparing the results of the optimal control and without control, the media coverage should be controlled according to the optimal control measures shown in this paper. The serious situation of game addiction will be greatly alleviated, which can reduce the infection rate by at least 90%.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Borzikowsky, C., Bernhardt, F.: Lost in virtual gaming worlds: Grit and its prognostic value for online game addiction. Am. J. Addict. 27(5), 433–438 (2018)

    Article  Google Scholar 

  2. Tang, C.S., Koh, Y.W., Gan, Y.Q.: Addiction to internet use, online gaming, and online social networking among young adults in China, Singapore, and the United States. Asia Pac. J. Public Health 29, 673–682 (2017)

    Article  Google Scholar 

  3. World Health Statistics 2019 (2019). https://www.who.int/gho/publications/world/health/statistics/2018/en/. Accessed 7 Apr 2019

  4. Zajac, K., Ginley, M.K., Chang, R.: Treatments of internet gaming disorder: a systematic review of the evidence. Expert Rev. Neurother. 20(1), 85–93 (2020)

    Article  Google Scholar 

  5. Wang, J., Zhang, J., Jin, Z.: Analysis of an SIR model with bilinear incidence rate. Nonlinear Anal. Real World Appl. 11(4), 2390–2402 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  6. Yan, Q., Tang, S., Gabriele, S., Wu, J.: Media coverage and hospital notifications: correlation analysis and optimal media impact duration to manage a pandemic. J. Theor. Biol. 390, 1–13 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. Huo, H., Zhang, X.: Stability and bifurcation for an SEIS epidemic model with the impact of media. Physica A 490, 702–720 (2018)

    Article  MathSciNet  Google Scholar 

  8. Liu, R., Wu, J., Zhu, H.: Media/psychological impact on multiple outbreaks of emerging infectious diseases. Comput. Math. Methods Med. 8(3), 153–164 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. Xiao, D., Ruan, S.: Global analysis of an epidemic model with nonmonotone incidence rate. Math Biosci. 208(2), 419–429 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Guo, W., Cai, Y., Zhang, Q., Wang, W.: Stochastic persistence and stationary distribution in an SIS epidemic model with media coverage. Physica A 492, 2220–2236 (2018)

    Article  MathSciNet  Google Scholar 

  11. Xiao, Y., Tang, S., Wu, J.: Media impact switching surface during an infectious disease outbreak. Sci. Rep. UK 5, 7838 (2015)

    Article  Google Scholar 

  12. Khan, M.A., Shah, S.W., Ullah, S., Gómez-Aguilar, J.F.: A dynamical model of asymptomatic carrier Zika virus with optimal control strategies. Nonlinear Anal. Real World Appl. 50, 144–170 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  13. Das, D.K., Khajanchi, S., Kar, T.K.: The impact of the media awareness and optimal strategy on the prevalence of tuberculosis. Appl. Math. Comput. 366, 124732 (2020)

    MathSciNet  MATH  Google Scholar 

  14. Jan, R., Khan, M.A., Gómez-Aguilar, J.F.: Asymptomatic carriers in transmission dynamics of dengue with control interventions. Comput. Optim. Appl. 2019, 1–18 (2019)

    Google Scholar 

  15. Khan, M.A., Islam, S., Zaman, G.: Media coverage campaign in Hepatitis B transmission model. Appl. Math. Comput. 331, 378–393 (2018)

    MathSciNet  MATH  Google Scholar 

  16. Li, T., Guo, Y.: Stability and optimal control in a mathematical model of online game addiction. Filomat 33(17), 5691–5711 (2019)

    Article  MathSciNet  Google Scholar 

  17. Lu, Z.: From E-heroin to E-sports: the development of competitive gaming in China. Int. J. History Sport 33(18), 2186–2206 (2017)

    Article  Google Scholar 

  18. Pang, L., Zhao, Z., Song, X.: Cost-effectiveness analysis of optimal strategy for tumor treatment. Chaos Soliton Fractals 87, 293–301 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  19. Driessche, P.V., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  20. Fleming, W.H., Rishel, R.W.: Deterministic and Stochastic Optimal Control. Springer, New York (1975)

    Book  MATH  Google Scholar 

  21. The 43rd statistical report on internet development in China. http://www.cac.gov.cn. Accessed 28 Feb 2019

  22. Fatoorehchi, H., Alidadi, M., Rach, R., Shojaeian, A.: Theoretical and experimental investigation of thermal dynamics of Steinhart–Hart negative temperature coefficient thermistors. J. Heat Transf. 141(7), 072003 (2019)

    Article  Google Scholar 

  23. Fatoorehchi, H., Rach, R., Sakhaeinia, H.: Explicit Frost-Kalkwarf type equations for calculation of vapour pressure of liquids from triple to critical point by the Adomian decomposition method. Can. J. Chem. Eng. 95(11), 2199–2208 (2017)

    Article  Google Scholar 

  24. Makinde, O.D.: Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 184(2), 842–848 (2007)

    MathSciNet  MATH  Google Scholar 

  25. González-Parra, G., Arenas, A.J., Jódar, L.: Piecewise finite series solutions of seasonal diseases models using multistage Adomian method. Commun. Nonlinear Sci. 14, 3967–3977 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Fatoorehchi, H., Abolghasemi, H.: An explicit analytic solution to the Thomas-Fermi equation by the improved differential transform method. Acta Phys. Pol. A 125(5), 1083–1087 (2014)

    Article  Google Scholar 

  27. Arenas, A.J., González-Parra, G., Chen-Charpentier, B.M.: Dynamical analysis of the transmission of seasonal diseases using the differential transformation method. Acta Phys. Pol. A 50(5), 765–776 (2009)

    MathSciNet  MATH  Google Scholar 

  28. LaSalle, J.P.: The stability of dynamical systems. In: Regional Conference Series in Applied Mathematics. SIAM, Philadelphia (1976)

  29. Lukes, D.L.: Differential Equations: Classical to Controlled, Mathematics in Science and Engineering. Academia Press, New York (1982)

    Google Scholar 

  30. Sana, M., Saleem, R., Manaf, A., Habib, M.: Varying forward backward sweep method using Runge-Kutta, Euler and Trapezoidal scheme as applied to optimal control problems. Sci. Int. (Labore) 27(2), 839–843 (2015)

    Google Scholar 

  31. Guo, Y., Li, T.: Optimal control and stability analysis of an online game addiction model with two stages. Math. Methods App Sci. 1, 1–18 (2020)

    MathSciNet  MATH  Google Scholar 

  32. Okosun, K.O., Khan, M.A., Bonyah, E., Okosun, O.O.: Cholera-schistosomiasis coinfection dynamics. Optim. Control Appl. Methods 40(4), 703–727 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  33. Yıldız, T.A., Karaoǧlu, E.: Optimal control strategies for tuberculosis dynamics with exogenous reinfections in case of treatment at home and treatment in hospital. Nonlinear Dyn. 97(4), 2643–2659 (2019)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the editor and the reviewers for their valuable comments and suggestions. This work was supported by Basic Competence Promotion Project for Young and Middle-aged Teachers in Guangxi, China (2019KY0269).

Author information

Authors and Affiliations

  1. College of Science, Guilin University of Technology, Guilin, 541004, Guangxi, People’s Republic of China

    Tingting Li & Youming Guo

Authors
  1. Tingting Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Youming Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Youming Guo.

Ethics declarations

Conflict of interest

There are no conflicts of interest by the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by the Basic Competence Promotion Project for Young and Middle-aged Teachers in Guangxi, China (2019KY0269).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, T., Guo, Y. Optimal control of an online game addiction model with positive and negative media reports. J. Appl. Math. Comput. 66, 599–619 (2021). https://doi.org/10.1007/s12190-020-01451-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01451-3

Keywords

Mathematics Subject Classification

Search

Navigation