Skip to main content
Springer Nature Link
Log in

Modeling the transmission dynamics of malaria with saturated treatment: a case study of India

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

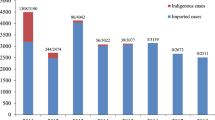
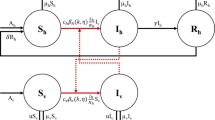
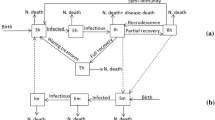
Malaria is a life-threatening mosquito-borne disease. It is transmitted through the bite of an infected Anopheles mosquito. Malaria may be fatal if not treated promptly. Malaria is a major public health problem in India. Here we propose an SIRS model to study the transmission dynamics of malaria with saturated treatment. We assume that the mosquito population is growing logistically in the environment. Here we include a saturated type treatment function which is more suitable for the regions with limited resources. We discuss the existence and stability of different equilibria of the proposed model. We also compute the basic reproduction number \(R_0\) which plays an important role in existence and stability of equilibria of the model. For \(R_0 < 1\), backward bifurcation occurs, which suggests that lowering \(R_0\) below one is not enough to eliminate the disease from the population. We estimate the key parameter corresponding to transmission of malaria using real data from different states of India by least square method. We also perform sensitivity analysis using PRCC to identify the key parameters which influence the infection prevalence of the disease and the basic reproduction number. Numerical simulations are presented to illustrate the analytic findings. Our numerical results suggest that infected population should get proper treatment and increase in the death rate of mosquito can also help to eradicate the malaria disease from the population.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. WHO.: Facts about malaria (2019), https://www.who.int/news-room/facts-in-pictures/detail/malaria

  2. National Vector Borne Disease Control Programme.: (2003), https://nvbdcp.gov.in/index1.php?lang=1&level=1&sublinkid=5784&lid=3689

  3. Malaria Site.: Malaria in India (2019), https://www.malariasite.com/malaria-india/

  4. Beretta, E., Capasso, V., Garao, D.G.: A mathematical model for malaria transmission with asymptomatic carriers and two age groups in the human population. Math. Biosci. 303, 155–156 (2018)

    Article  MathSciNet  Google Scholar 

  5. Wang, L., Teng, Z., Ji, C., Feng, X., Wang, K.: Dynamical behaviors of a stochastic malaria model: a case study for Yunnan. China. Phys. Stat. Mech. Appl. 521, 435–454 (2019). https://doi.org/10.1016/j.physa.2018.12.030

    Article  MathSciNet  Google Scholar 

  6. Agusto, F.B., Valle, S.Y.D., Blayneh, K.W., Ngonghala, C.N., Goncalves, M.J., Li, N., Zhao, R., Gong, H.: The impact of bed-net use on malaria prevalence. J. Theor. Biol. 320, 58–65 (2013)

    Article  Google Scholar 

  7. Chitnis, N., Cushing, J.M., Hyman, J.M.: Bifurcation analysis of a mathematical model for malaria transmission. SIAM J. Appl. Math. 67, 24–25 (2006)

    Article  MathSciNet  Google Scholar 

  8. Gratz, N.: Emergency control of Aedes aegypti as a disease vector in urban areas. J. Am. Mosq. Control Assoc. 7(3), 353–365 (1991)

    Google Scholar 

  9. Ghosh, M.: The spread of malaria with human reservoir: effect of environmental discharges. J. Adv. Res. Dyn. Control Syst. 6(3), 79–100 (2014)

    MathSciNet  Google Scholar 

  10. Orwa, T.O., Mbogo, R.W., Luboobi, L.S.: Mathematical model for the in-host malaria dynamics subject to malaria vaccines. Lett. Biomath. 5(1), 222–251 (2018). https://doi.org/10.1080/23737867.2018.1526132

    Article  MathSciNet  MATH  Google Scholar 

  11. Mandal, S., Sarkar, R.R., Sinha, S.: Mathematical models of malaria: a review. Malaria J 10, 1–19 (2011)

    Article  Google Scholar 

  12. Chiyaka, C., Tchuenche, J.M., Garira, W., Dube, S.: A mathematical analysis of the effects of control strategies on the transmission dynamics of malaria. Appl. Math. Comput. 195(3), 641–662 (2008)

    MathSciNet  MATH  Google Scholar 

  13. Mwanga, G., Haario, H., Capasso, V.: Optimal control problems of epidemic systems with parameter uncertainties: application to a malaria two-age-classes transmission model with asymptomatic carriers. Math. Biosci. 261, 1–12 (2015)

    Article  MathSciNet  Google Scholar 

  14. Agusto, F.B., Marcus, N., Okosun, K.O.: Application of optimal control to the epidemiology of malaria. Electr. J. Differ. Equ. 2012(81), 1–22 (2012)

    MathSciNet  MATH  Google Scholar 

  15. Athitan, S., Ghosh, M.: Stability analysis and optimal control of a malaria model with larvivorous fish as biological control agent. Appl. Math. Inf. Sci. 9(4), 1893–1913 (2015)

    MathSciNet  Google Scholar 

  16. Cai, L., Li, X.Z., Tuncer, N., Martcheva, M., Lashari, A.A.: Optimal control of a malaria model with asymptomatic class and superinfection. Math. Biosci. 288, 94–108 (2017)

    Article  MathSciNet  Google Scholar 

  17. Cai, L., Tuncer, N., Martcheva, M.: How does within-host dynamics affect population-level dynamics? Insights from an immuno-epidemiological model of malaria. Math. Methods Appl. Sci. 40(18), 6424–6450 (2017)

    Article  MathSciNet  Google Scholar 

  18. Bhatt, S., Weiss, D., Cameron, E., Bisanzio, D., Mappin, B., Dalrymple, U., Wenger, E.A.: The effect of malaria control on Plasmodium falciparum in Africa between 2000 and 2015. Nature 526(7572), 207 (2015)

    Article  Google Scholar 

  19. Cai, L., Huang, J., Song, X., Zhang, Y.: Bifurcation analysis of a mosquito population model for proportional releasing sterile mosquitoes. Discr. Contin. Dyn. Syst. Seri. B 24, 6279–6295 (2019)

    MathSciNet  MATH  Google Scholar 

  20. Cai, L., Li, Z., Liu, J.: Modeling and analyzing dynamics of malaria transmission with host immunity. Int. J. Biomath. 12(6), 1950074 (2019)

    Article  MathSciNet  Google Scholar 

  21. Cai, L., Ai, S., Fan, G.: Dynamics of delayed mosquitoes populations models with two different strategies of releasing sterile mosquitoes. Math. Biosci. Eng. 15(5), 1181–1202 (2018). https://doi.org/10.3934/mbe.2018054

    Article  MathSciNet  MATH  Google Scholar 

  22. Feng, W.J., Cai, L., Liu, K.: Dynamics of a dengue epidemic model with class-age structure. Int. J. Biomath. 10(08), 1750109 (2017)

    Article  MathSciNet  Google Scholar 

  23. Dubey, B., Patra, A., Srivastava, P.K., Dubey, U.S.: Modeling and analysis of an SEIR model with different types of nonlinear treatment rates. J. Biol. Syst. (2013). https://doi.org/10.1142/S021833901350023X

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhang, X., Liu, X.: Backward bifurcation of an epidemic model with saturated treatment function. J. Math. Anal. Appl. 348(1), 433–443 (2008)

    Article  MathSciNet  Google Scholar 

  25. Li, X.-Z., Li, W.S., Ghosh, M.: Stability and bifurcation of an SIS epidemic model with treatment. Chaos Solit. Fract. 42(5), 2822–2832 (2009)

    Article  MathSciNet  Google Scholar 

  26. Gao, L.Q., Hethcote, H.W.: Disease transmission models with density dependent demographics. J. Math. Biol. 32, 717–731 (1992)

    MathSciNet  MATH  Google Scholar 

  27. Driessche, P.V., Watmough, J.: Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)

    Article  MathSciNet  Google Scholar 

  28. Bakary, T., Boureima, S., Sado, T.: A mathematical model of malaria transmission in a periodic environment. J. Biol. Dyn. 12(1), 400–432 (2018). https://doi.org/10.1080/17513758.2018.1468935

    Article  MathSciNet  MATH  Google Scholar 

  29. Mukhtar, A.Y.A., Munyakazi, J.B., Ouifki, R.: Assessing the role of climate factors on malaria transmission dynamics in South Sudan. Math. Biosci. 310, 13–23 (2019)

    Article  MathSciNet  Google Scholar 

  30. Castillo-Chavez, C., Song, B.: Dynamical model of tuberculosis and their applications. Math. Biosci. Eng. 1, 361–404 (2004)

    Article  MathSciNet  Google Scholar 

  31. National Health Portal of India, https://www.nhp.gov.in/world-malaria-day-2018, Visited on Jan 10, 2019

  32. Blower, S.M., Dowlatabadi, H.: Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example. Int. Stat. Rev. 62, 229–243 (1994)

    Article  Google Scholar 

  33. Marino, S., Hogue, I.B., Ray, C.J., Kirschner, D.E.: A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254, 178–196 (2008)

    Article  MathSciNet  Google Scholar 

  34. Ngonghala, C.N., Del Valle, S.Y., Zhao, R., Mohammed-Awel, J.: Quantifying the impact of decay in bednets efficacy on malaria transmission. J. Theor. Biol. 364, 247–261 (2014)

    Article  Google Scholar 

  35. Ngonghala, C.N., Mohammed, J., Zhao, R., Prosper, O.: Interplay between insecticide-treated bednets and mosquito demography: implications for malaria control. J. Theor. Biol. 397, 179–192 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

The authors thank the handling editor and anonymous referees for their valuable comments and suggestions that led to an improvement of our original manuscript. This research was supported by the research grants of DST, Govt. of India, via a sponsored research project: FILE NO. EMR/2017/003139.

Author information

Authors and Affiliations

  1. Division of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, Chennai, India

    Akhil Kumar Srivastav & Mini Ghosh

Authors
  1. Akhil Kumar Srivastav
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mini Ghosh
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mini Ghosh.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Srivastav, A.K., Ghosh, M. Modeling the transmission dynamics of malaria with saturated treatment: a case study of India. J. Appl. Math. Comput. 67, 519–540 (2021). https://doi.org/10.1007/s12190-020-01469-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01469-7

Keywords

Mathematics Subject Classification