Skip to main content

Advertisement

Springer Nature Link
Log in

Extremal phenylene chains with respect to detour indices

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

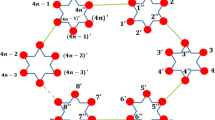
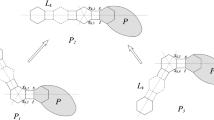
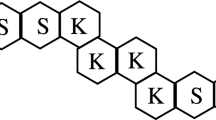
Computing topological indices of molecular structures is a fundamental and classical topic. In organic chemistry, hexagonal and quadrilateral molecular structures are very common. The detour index \(\omega (G)\) of a connected graph G is defined as \(\omega (G)=\sum \nolimits _{\{u,v\}\subseteq V(G)}l_{G}(u,v)\), where \(l_{G}(u,v)\) denotes the detour distance between vertices u and v. In this study, we obtain the explicit analytical expression for detour index of phenylene chains with a fixed number of hexagons. Further minimal and maximal phenylene chains are obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Amić, D., Trinajstić, N.: On detour matrix. Croat. Chem. Acta 68, 53–62 (1995)

    MathSciNet  Google Scholar 

  2. Chen, H., Guo, Q.: Tutte polynomials of alternating polyclic chains. J. Math. Chem. 57, 2248–2260 (2019)

    Article  MathSciNet  Google Scholar 

  3. Chen, A., Zhang, F.: Wiener index and perfect matchings in random phenylene chains. MATCH Commun. Math. Comput. Chem. 61, 623–630 (2009)

    MathSciNet  MATH  Google Scholar 

  4. Du, C.: Minimum detour index of bicyclic graphs. MATCH Commun. Math. Comput. Chem. 68, 357–370 (2012)

    MathSciNet  MATH  Google Scholar 

  5. Deng, H., Chen, S., Zhang, J.: The PI index of phenylenes. J. Math. Chem. 41, 63–69 (2007)

    Article  MathSciNet  Google Scholar 

  6. Fang, W., Cai, Z.Q., Li, X.X.: Minimum detour index of tricyclic graphs. J. Chem. 6031568 (2019)

  7. Furtula, B., Gutman, I.: Energy and Estrada index of phenylenes. Indian. J. Chem. A. 47, 220–224 (2008)

    Google Scholar 

  8. Furtula, B., Gutman, I., Zeljko, T., Vesel, A., Pesek, I.: Wiener-type topological indices of phenylenes. Indian. J. Chem. A. 41, 1767–1772 (2002)

    Google Scholar 

  9. Gutman, I., Furtula, B.: A Kekulé structure basis for phenylenes. J. Mol. Struct. 770, 67–71 (2006)

    Article  Google Scholar 

  10. Gutman, I., Ashrafi, A.R.: On the PI index of phenylenes and their hexagonal squeezes. MATCH Commun. Math. Comput. Chem. 60, 135–142 (2008)

    MathSciNet  MATH  Google Scholar 

  11. Gutman, I., Klavžar, S.: Relations between Wiener numbers of benzenoid hydrocarbons and phenylenes. ACH Models Chem. 135, 45–55 (1998)

    Google Scholar 

  12. Lukovits, I.: The detour index. Croat. Chem. Acta 69, 873–882 (1996)

    Google Scholar 

  13. Milosavljevic, N., Stevanovic, D.: Detour index of hexagonal chains. MATCH Commun. Math. Comput. Chem. 72, 137–152 (2014)

    MathSciNet  MATH  Google Scholar 

  14. Nikolić, S., Trinajstić, N., Mihalić, Z.: The Wiener index: developments and applications. Croat. Chem. Acta 68, 105–129 (1995)

    Google Scholar 

  15. Qi, X., Zhou, B.: Detour index of a class of unicyclic graphs. Filomat 24, 29–40 (2010)

    Article  MathSciNet  Google Scholar 

  16. Qi, X., Zhou, B.: Maximum detour index of unicyclic graphs with given maximum degree. ARS Combin. 102, 193–200 (2011)

    MathSciNet  MATH  Google Scholar 

  17. Qi, X., Zhou, B.: Hyper-detour index of unicyclic graphs. MATCH Commun. Math. Comput. Chem. 66, 329–342 (2011)

    MathSciNet  MATH  Google Scholar 

  18. Raza, Z.: The expected values of arithmetic bond connectivity and geometric indices in random phenylene chains. Heliyon 6, e04479 (2020)

    Article  Google Scholar 

  19. Trinajstić, N., Nikolić, S., Lučić, B., Amić, D., Mihalić, Z.: The detour matrix in chemistry. J. Chem. Inf. Comput. Sci. 37, 631–638 (1997)

    Article  Google Scholar 

  20. Vollhardt, K.P.C.: The phenylenes. Pure Appl. Chem. 65, 153–156 (1993)

    Article  Google Scholar 

  21. Wiener, H.: Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69, 17–20 (1947)

    Article  Google Scholar 

  22. Zhou, B., Cai, X.: On detour index. MATCH Commun. Math. Comput. Chem. 63, 199–210 (2010)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, South China Normal University, Guangzhou, 510631, People’s Republic of China

    Hechao Liu & Xiaona Fang

Authors
  1. Hechao Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaona Fang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hechao Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Research supported by the National Natural Science Foundation of China (through Grant No. 11971180, 11571123), the Guangdong Provincial Natural Science Foundation of China (through Grant No. 2019A1515012052).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, H., Fang, X. Extremal phenylene chains with respect to detour indices. J. Appl. Math. Comput. 67, 301–316 (2021). https://doi.org/10.1007/s12190-020-01483-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01483-9

Keywords

Mathematics Subject Classification