Skip to main content
Springer Nature Link
Log in

An application of a novel geometric criterion to global-stability problems of a nonlinear SEIVS epidemic model

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

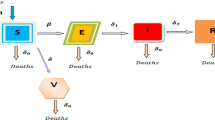
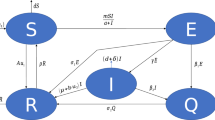
This work applies a novel geometric criterion for nonlinear autonomous differential equations developed by Lu and Lu (NARWA 36:20–43, 2017) to a nonlinear SEIVS epidemic model with temporary immunity and achieves its threshold dynamics. Specifically, global-stability problems for the SEIVS model of Cai and Li (AMM 33:2919–2926, 2009) are effectively solved. The corresponding optimal control system with vaccination, awareness campaigns and treatment is further established and four different control strategies are compared by numerical simulations to contain hepatitis B. It is concluded that joint implementation of these measures can minimize the numbers of exposed and infectious individuals in the shortest time, so it is the most efficient strategy to curb the hepatitis B epidemic. Moreover, vaccination for newborns plays the core role and maintains the high level of population immunity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Krämer, A., Kretzschmar, M., Krickeberg, K.: Modern infectious disease epidemiology: concepts, methods, mathematical models, and public health. Springer, Berlin, Germany (2010)

    Book  MATH  Google Scholar 

  2. WHO, Immunization coverage, 2020. Available from: https://www.who.int/news-room/fact-sheets/detail/immunization-coverage Accessed 7 December 2020

  3. Cai, L.M., Li, X.Z.: Analysis of a SEIV epidemic model with a nonlinear incidence rate. Appl. Math. Model. 33(7), 2919–2926 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  4. Sahu, G.P., Dhar, J.: Analysis of an SVEIS epidemic model with partial temporary immunity and saturation incidence rate. Appl. Math. Model. 36(3), 908–923 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cai, L.M., Li, Z.Q., Song, X.Y.: Global analysis of an epidemic model with vaccination. J. Appl. Math. Comput. 57(1), 605–628 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  6. Lahrouz, A., Omari, L., Kiouach, D., Belmaâtic, A.: Complete global stability for an SIRS epidemic model with generalized non-linear incidence and vaccination. Appl. Math. Comput. 218(11), 6519–6525 (2012)

    MathSciNet  MATH  Google Scholar 

  7. Li, T., Zhang, F.Q., Liu, H.W., Chen, Y.M.: Threshold dynamics of an SIRS model with nonlinear incidence rate and transfer from infectious to susceptible. Appl. Math. Lett. 70, 52–57 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  8. Liu, W.M., Levin, S.A., Iwasa, Y.: Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 23(2), 187–204 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  9. Lu, M., Huang, J.C., Ruan, S.G., Yu, P.: Bifurcation analysis of an SIRS epidemic model with a generalized nonmonotone and saturated incidence rate. J. Differ. Equ. 267(3), 1859–1898 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  10. Capasso, V., Serio, G.: A generalization of the Kermack–McKendrick deterministic epidemic model. Math. Biosci. 42, 43–61 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  11. Xiao, D.M., Ruan, S.G.: Global analysis of an epidemic model with a nonlinear incidence rate. Math. Biosci. 208(2), 419–429 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Khan, M.A., Ullah, S., Khan, Y., Farhan, M.A.: Modeling and scientific computing for the transmission dynamics of avian influenza with half-saturated incidence. Int. J. Model Simul. Sci. Comput. 11(4), 2050035 (2020)

    Article  Google Scholar 

  13. Anderson, R.M., May, R.M.: Infectious diseases of humans: dynamics and control. Oxford University Press, London (1991)

    Google Scholar 

  14. Lu, G.C., Lu, Z.Y.: Geometric approach to global asymptotic stability for the SEIRS models in epidemiology. Nonlinear Anal. Real World Appl. 36, 20–43 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  15. Lu, G.C., Lu, Z.Y.: Global asymptotic stability for the SEIRS models with varying total population size. Math. Biosci. 296, 17–25 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, M.Y., Muldowney, J.S.: A geometric approach to the global-stability problems. SIAM J. Math. Anal. 27(4), 1070–1083 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  17. Li, M.Y., Graef, J.R., Wang, L.C., Karsai, J.: Global dynamics of a SEIR model with varying total population size. Math. Biosci. 160, 191–213 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, M.Y., Muldowney, J.S.: Dynamics of differential equations on invariant manifolds. J. Differ. Equ. 168, 295–320 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Doungmo Goufo, E.F., Khan, Y., Chaudhry, Q.A.: HIV and shifting epicenters for COVID-19, an alert for some countries. Chaos Solitons Fractals 139, 110030 (2020)

    Article  MathSciNet  Google Scholar 

  20. Khan, M.A., Khan, Y., Islam, S.: Complex dynamics of an SEIR epidemic model with saturated incidence rate and treatment. Phys. A 493, 210–227 (2018)

    Article  MathSciNet  Google Scholar 

  21. Khan, M.A., Khan, R., Khan, Y., Islam, S.: A mathematical analysis of Pine Wilt disease with variable population size and optimal control strategies. Chaos Solitons Fractals 108, 205–207 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Khan, M.A., Iqbal, N., Khan, Y., Alzahrani, E.: A biological mathematical model of vector-host disease with saturated treatment function and optimal control strategies. Math. Biosci. Eng. 17(4), 3972–3997 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  23. Arino, J., Cooke, K.L., van den Driessche, P., Velasco-Hernndez, J.: An epidemiology model that includes a leaky vaccine with a general waning function. Discrete Cont. Dyn. Syst. Ser. B 4(2), 479–495 (2004)

    MathSciNet  MATH  Google Scholar 

  24. Huo, J.J., Zhao, H.Y., Zhu, L.H.: The effect of vaccines on backward bifurcation in a fractional order HIV model. Nonlinear Anal. Real World Appl. 26, 289–305 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. WHO: Global tuberculosis report 2020, (2020). Available from: https://www.who.int/publications/i/item/9789240013131 Accessed 7 December 2020

  26. Wang, L.W., Liu, Z.J., Xu, D.S., Zhang, X.A.: Global dynamics and optimal control of an influenza model with vaccination, media coverage and treatment. Int. J. Biomath. 10, 1750068 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  27. Graber-Stiehl, I.: The silent epidemic killing more people than HIV, malaria or TB. Nature 564(7734), 24–26 (2018)

    Article  Google Scholar 

  28. Lazarus, J.V., Picchio, C., Dillon, J.F., Rockstroh, J.K., Weis, N., Buti, M.: Too many people with viral hepatitis are diagnosed late-with dire consequences. Nat. Rev. Gastroenterol Hepatol 16, 451–452 (2019)

    Article  Google Scholar 

  29. Pontryagin, L., Boltyanskii, V., Gramkrelidze, R., Mischenko, E.: The mathematical theory of optimal processes. Wiley, New York (1962)

    Google Scholar 

  30. Fleming, W.H., Rishel, R.W.: Deterministic and stochastic optimal control. Springer, Berlin (1975)

    Book  MATH  Google Scholar 

  31. Pang, L.Y., Ruan, S.G., Liu, S.H., Zhao, Z., Zhang, X.A.: Transmission dynamics and optimal control of measles epidemics. Appl. Math. Comput. 256, 131–147 (2015)

    MathSciNet  MATH  Google Scholar 

  32. Wang, X.W., Peng, H.J., Shi, B.Y., Jiang, D.H., Zhang, S., Chen, B.S.: Optimal vaccination strategy of a constrained time-varying SEIR epidemic model. Commun. Nonlinear Sci. Numer. Simul. 67, 37–48 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  33. Yang, J.Y., Modnak, C., Wang, J.: Dynamical analysis and optimal control simulation for an age-structured cholera transmission model. J. Franklin. I 356, 8438–8467 (2019)

  34. Lv, W., Ke, Q., Li, K.Z.: Dynamic stability of an SIVS epidemic model with imperfect vaccination on scale-free networks and its control strategy. J. Franklin. I 357, 7092–7121 (2020)

  35. Djidjou Demasse, R., Tewa, J.J., Bowong, S., Emvudu, Y.: Optimal control for an age-structured model for the transmission of hepatitis B. J. Math. Biol. 73(2), 305–333 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  36. Melesse, D.Y., Gumel, A.B.: Global asymptotic properties of an SEIRS model with multiple infectious stages. J. Math. Anal. Appl. 366, 202–217 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Khan, M.A., Khan, Y., Khan, T.W.: Dynamical system of a SEIQV epidemic model with nonlinear generalized incidence rate arising in biology. Int. J. Biomath. 10(7), 1750096 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  38. Liu, J.L., Zhang, T.L.: Global stability for a tuberculosis model. Math. Comput. Model. 54, 836–845 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  39. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  40. LaSalle, J.P.: The stability of dynamical systems, in: regional conference series in Applied Mathematics. SIAM, Philadephia (1976)

    Book  Google Scholar 

  41. Tian, Y.N., Liu, X.N.: Global dynamics of a virus dynamical model with general incidence rate and cure rate. Nonlinear Anal. Real World Appl. 16, 17–26 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  42. Bi, K.M., Chen, Y.Y., Wu, C.H.J., Ben-Arieh, D.: A memetic algorithm for solving optimal control problems of Zika virus epidemic with equilibriums and backward bifurcation analysis. Commun. Nonlinear Sci. Numer. Simul. 84, 105176 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  43. World Health Statistics 2020 visual summary. Available from: https://www.who.int/data/gho/whs-2020-visual-summary Accessed 7 December 2020

  44. Pang, J., Cui, J.A., Zhou, X.: Dynamical behavior of a hepatitis B virus transmission model with vaccination. J. Theor. Biol. 265(4), 572–578 (2010)

    Article  MathSciNet  Google Scholar 

  45. Edmunds, W.J., Medley, G.F., Nokes, D.J.: The transmission dynamics and control of hepatitis B virus in the Gambia. Stat. Med. 15, 2215–2233 (1996)

    Article  Google Scholar 

  46. Zou, L., Zhang, W.N., Ruan, S.G.: Modeling the transmission dynamics and control of hepatitis B virus in China. J. Theor. Biol. 262, 330–338 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  47. Liu, W.M., Hethcote, H.W., Levin, S.A.: Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 25, 359–380 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  48. Khan, Y., Faraz, N., Kumar, S., Yildirim, A.: A coupling method of homotopy perturbation and laplace transformation for fractional models. U.P.B. Sci. Bull. Series A 74(1), 57–68 (2012)

    MathSciNet  MATH  Google Scholar 

  49. Khan, Y., Faraz, N., Yildirim, A., Wu, Q.B.: Fractional variational iteration method for fractional initial-boundary value problems arising in the application of nonlinear science. Comput. Math. Appl. 62, 2273–2278 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  50. Khan, Y., Wu, Q.B., Faraz, N., Yildirim, A., Madanie, M.: A new fractional analytical approach via a modified Riemann-Liouville derivative. Appl. Math. Lett. 25, 1340–1346 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  51. Khan, Y., Latifizadeh, H.: Application of new optimal homotopy perturbation and adomian decomposition methods to the MHD non-Newtonian fluid flow over a stretching sheet. Int. J. Numer. Method H. 24, 124–136 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  52. Khan, Y.: A method for solving nonlinear time-dependent drainage model. Neural Comput. Appl. 23, 411–415 (2013)

    Article  Google Scholar 

  53. Khan, Y., Vázquez-Leal, H., Wu, Q.: An efficient iterated method for mathematical biology model. Neural Comput. Appl. 23, 677–682 (2013)

    Article  Google Scholar 

  54. Khan, Y., Wu, Q.B.: Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 61, 1963–1967 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  55. Khan, Y.: Two-dimensional boundary layer flow of chemical reaction MHD fluid over a shrinking sheet with suction and injection. J. Aerosp. Eng. Trans. ASCE 27, 04014019 (2014)

    Article  Google Scholar 

  56. Khan, Y., Vázquez-Leal, H., Faraz, N.: An auxiliary parameter method using adomian polynomials and laplace transformation for nonlinear differential equations. Appl. Math. Model. 37, 2702–2708 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The work is supported by Natural Science Foundation of Hubei Province (Nos. 2019CFB241, 2019CFB773) and National Natural Science Foundation of China (Nos. 11871201,11961023).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Hubei Minzu University, Enshi, 445000, People’s Republic of China

    Xingyu Wang, Zhijun Liu, Lianwen Wang & Huili Xiang

  2. Enshi Special Care Hospital, Enshi, 445000, People’s Republic of China

    Caihong Guo

Authors
  1. Xingyu Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhijun Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Lianwen Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Caihong Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Huili Xiang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Lianwen Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Liu, Z., Wang, L. et al. An application of a novel geometric criterion to global-stability problems of a nonlinear SEIVS epidemic model. J. Appl. Math. Comput. 67, 707–730 (2021). https://doi.org/10.1007/s12190-020-01487-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01487-5

Keywords