Skip to main content
Springer Nature Link
Log in

Randic index of bipolar fuzzy graphs and its application in network systems

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

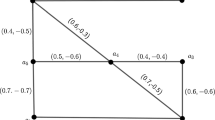
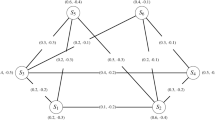
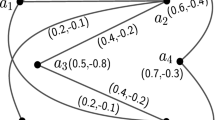
Abstract

Connectivity can be used to measure the strength and combined power of a connected network system. Randic index of graph is one such parameter and it can measure the total combined power of a connected graphical transmission system. For two opposite sided opinion of vertices as well as edges in a bipolar fuzzy graph, it can measure the uncertainty of vertices and edges along positive and negative sides. In this article, the Randic index of bipolar fuzzy graph and bipolar fuzzy subgraph are introduced with their properties. The upper and lower boundaries of Randic index of bipolar fuzzy graphs are studied with some isomorphic properties. Randic index of directed bipolar fuzzy graphs are introduced. Several formula’s are presented to calculate the Randic index of different types of regular bipolar fuzzy graphs and bipolar fuzzy cycles. Finally, two real life applications of Randic index in bipolar fuzzy graphs are described.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Akram, M.: Bipolar fuzzy graphs. Inf. Sci. 181(24), 5548–5564 (2011)

    Article  MathSciNet  Google Scholar 

  2. Akram, M.: Bipolar fuzzy graphs with applications. Knowl. Based Syst. 39, 1–8 (2013)

    Article  Google Scholar 

  3. Akram, M.: \(m\)-Polar Fuzzy Graphs: Theory. Methods & Applications. Springer, Berlin (2018)

    MATH  Google Scholar 

  4. Akram, M., Akmal, R., Alshehri, N.: On \(m\)-polar fuzzy graph structures. SpringerPlus 5, 1448 (2016)

    Article  Google Scholar 

  5. Akram, M., Ali, G., Butt, M.A., Alcantud, J.C.R.: Novel MCGDM analysis under \(m\)-polar fuzzy soft expert sets. Neural Comput. Appl. (2021). https://doi.org/10.1007/s00521-021-05850-w

    Article  Google Scholar 

  6. Akram, M., Amzad, U., Davvaz, B.: Decision-making analysis based on bipolar fuzzy \(N\)-soft information. Comput. Appl. Math. 40, 180 (2021)

    Article  MathSciNet  Google Scholar 

  7. Akram, M., Farooq, A.: Bipolar fuzzy tree. New Trends Math. Sci. 4(3), 58–72 (2016)

    Article  MathSciNet  Google Scholar 

  8. Akram, M., Karunambigal, M.G.: Metric in bipolar fuzzy graphs. World Appl. Sci. J. 14(12), 1920–1927 (2011)

    Google Scholar 

  9. Akram, M., Sarwar, M., Dudek, W.A.: Graphs for the Analysis of Bipolar Fuzzy Information. Springer, Berlin (2020)

    MATH  Google Scholar 

  10. Akram, M., Waseem, N.: Novel applications of bipolar fuzzy graphs to decision making problems. J. Appl. Math. Comput. 56, 73–91 (2018)

    Article  MathSciNet  Google Scholar 

  11. Binu, M., Mathew, S., Mordeson, J.N.: Wiener index of a fuzzy graph and application to illegal immigration networks. Fuzzy Sets Syst. 384, 132–147 (2020)

    Article  MathSciNet  Google Scholar 

  12. Cederbaum, I.: Some applications of graph theory to network analysis and synthesis. IEEE Trans. Circuits Syst. 31(1), 64–68 (1984)

    Article  Google Scholar 

  13. Das, S., Ghorai, G.: Analysis of the effect of medicines over bacteria based on competition graphs with picture fuzzy environment. Comput. Appl. Math. 39, 183 (2020)

    Article  MathSciNet  Google Scholar 

  14. Das, S., Ghorai, G., Pal, M.: Certain competition graphs based on picture fuzzy environment with applications. Artif. Intell. Rev. (2020). https://doi.org/10.1007/s10462-020-09923-5

    Article  MATH  Google Scholar 

  15. Ghorai, G., Pal, M.: A note on “Regular bipolar fuzzy graphs” Neural Comput. Appl 21(1), 197–205 (2012) Neural Comput. Appl. 30(5), 1569–1572 (2018)

  16. Ghorai, G., Pal, M.: Some isomorphic properties of \(m\)-polar fuzzy graphs with applications. SpringerPlus 5(1), 2104 (2016)

    Article  Google Scholar 

  17. Ghorai, G.: Characterization of regular bipolar fuzzy graphs. Afrika Matematika 32(5), 1043–1057 (2021)

    Article  MathSciNet  Google Scholar 

  18. Kaveh, A., Rahami, H., Shojaei, I.: Swift Analysis of Civil Engineering Structures Using Graph Theory Mathods. Springer, Berlin (2020)

    Book  Google Scholar 

  19. Masarwah, A.A., Qamar, M.A.: Some new concepts of fuzzy soft graphs. Fuzzy Inf. Eng. 8(4), 427–438 (2016)

    Article  MathSciNet  Google Scholar 

  20. Masarwah, A.A., Qamar, M.A.: Certain types of fuzzy soft graphs. New Math. Natural Comput. 14(02), 145–156 (2018)

    Article  MathSciNet  Google Scholar 

  21. Mathew, S., Sunitha, M.S., Anjali, N.: Some connectivity concepts in bipolar fuzzy graphs. Ann. Pure Appl. Math. 7(2), 98–100 (2014)

    Google Scholar 

  22. Mathew, S., Sunitha, M.S.: Types of arcs in a fuzzy graph. Inf. Sci. 179(11), 1760–1768 (2009)

    Article  MathSciNet  Google Scholar 

  23. Minoli, D.: Combinatorial graph complexity, Atti della Accademia Nazionale dei Lincei. Class di Scienze Fisiche. Matematiche e Naturali. Rendiconti 59(6):651–661 (1975)

  24. Mordeson, J.N., Nair, P.S.: Fuzzy Graphs and Fuzzy Hypergraphs. Physica-Verlag, Berlin (2000)

    Book  Google Scholar 

  25. Nawaz, H.S., Akram, M.: Oligopolistic competition among the wireless internet service providers of Malaysia using fuzzy soft graphs. J. Appl. math. Comput. (2021). https://doi.org/10.1007/s12190-021-01514-z

    Article  MathSciNet  MATH  Google Scholar 

  26. Poulik, S., Ghorai, G.: Certain indices of graphs under bipolar fuzzy environment with applications. Soft Comput. 24(7), 5119–5131 (2020)

    Article  Google Scholar 

  27. Poulik, S., Ghorai, G.: Determination of journeys order based on graphs Wiener absolute index with bipolar fuzzy information. Inf. Sci. 545, 608–619 (2021)

    Article  MathSciNet  Google Scholar 

  28. Poulik, S., Ghorai, G.: Detour g-interior nodes and detour g-boundary nodes in bipolar fuzzy graph with applications. Hacettepe J. Math. Stat. 49(1), 106–119 (2020)

    MathSciNet  MATH  Google Scholar 

  29. Poulik, S., Ghorai, G.: Empirical results on bipolar fuzzy graphs with their degree. Missouri J. Math. Sci. 32(2), 211–226 (2020)

    Article  MathSciNet  Google Scholar 

  30. Poulik, S., Ghorai, G.: Note on bipolar fuzzy graphs with applications. Knowl. Based Syst. 192, 1–5 (2020)

    Article  Google Scholar 

  31. Poulik, S., Ghorai, G., Xin, Q.: Pragmatic results in Taiwan education system based IVFG & IVNG. Soft Comput. (2020). https://doi.org/10.1007/s00500-020-05180-4

    Article  Google Scholar 

  32. Randic, M.: Characterization of molecular branching. J. Am. Chem. Soc. 97(23), 6609–6615 (1975)

    Article  Google Scholar 

  33. Rosenfield, A.: Fuzzy graphs. Fuzzy Sets and Their Application (L. A. Zadeh, K. S. Fu, M. Shimura, Eds.): Academic press, New York, 77-95, (1975)

  34. Shahzadi, S., Rasool, A., Sarwar, M., Akram, M.: A framework of decision making based on bipolar fuzzy competition hypergraphs. J. Intell. Fuzzy Syst. (2021). https://doi.org/10.3233/JIFS-210216

    Article  Google Scholar 

  35. Sarwar, M., Akram, M., Shahzadi, S.: Bipolar fuzzy soft information applied to hypergraphs. Soft Comput. 25(2), 1–23 (2021)

    Google Scholar 

  36. West, D.B.: Introduction to Graph Theory, Pearson Education India (2002)

  37. Yager, R.R., Alajlan, N.: Approximate reasoning with generalized orthopair fuzzy sets. Inf. Fusion 38, 65–73 (2017)

    Article  Google Scholar 

  38. Yager, R.R., Alajlan, N., Bazi, Y.: Aspects of generalized orthopair fuzzy sets. Int. J. Intell. Syst. 33(11), 2154–2174 (2018)

    Article  Google Scholar 

  39. Yang, H.L., Li, S.G., Yang, W.H., Lu, Y.: Notes on bipolar fuzzy graphs. Inf. Sci. 242, 113–121 (2013)

    Article  MathSciNet  Google Scholar 

  40. Yang, H.L., Li, S.G., Wang, S., Wang, J.: Bipolar fuzzy rough set model on two different universes and its application. Knowl. Based Syst. 35, 94–101 (2012)

    Article  Google Scholar 

  41. Zadeh, L.A.: Fuzzy sets. Inf Control 8(3), 338–353 (1965)

    Article  Google Scholar 

  42. Zhang, W.R.: Bipolar fuzzy sets and relations: a computational framework for cognitive modeling multiagent decision analysis. Proceeding of IEEE Conference 305–309 (1994)

  43. Zhang, X., Zhao, Y., Zhou, L., Dong, W., Zhang, M., Lv, X.: Transmission tower tilt monitoring system using low-power wide-area network technology. IEEE Sensors J. (2020). https://doi.org/10.1109/JSEN.2020.3004817

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to express their sincere gratitude to the anonymous referees for valuable suggestions, which led to great deal of improvement of the original manuscript. The first author is thankful to the Department of Higher Education, Science and Technology and Biotechnology, Government of West Bengal, India, for the award of Swami Vivekananda merit-cum-means scholarship (Award No. 52-Edn (B)/5B-15/2017 dated 07/06/2017) to meet up the financial expenditure to carry out the research work. The third author acknowledges the support of DST-FIST, New Delhi (India) (Sanction No. SR/FST/MS- I/2018/21) for carrying out this work.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics with Oceanology and Computer Programming, Vidyasagar University, Midnapore, 721 102, India

    Soumitra Poulik, Sankar Das & Ganesh Ghorai

  2. Department of Mathematics, Kharagpur College, Kharagpur, 721 305, India

    Sankar Das

Authors
  1. Soumitra Poulik
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Sankar Das
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ganesh Ghorai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ganesh Ghorai.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Poulik, S., Das, S. & Ghorai, G. Randic index of bipolar fuzzy graphs and its application in network systems. J. Appl. Math. Comput. 68, 2317–2341 (2022). https://doi.org/10.1007/s12190-021-01619-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-021-01619-5

Keywords