Skip to main content
SpringerLink
Log in

Landweber iteration method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

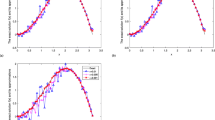
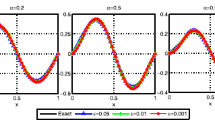
The present paper is devoted to identifying the space-dependent source term and initial value simultaneously for a time-fractional diffusion equation. This inverse problem is reformulated on the basis of Fourier method as operator equations of the first kind. The construction of the solution to the inverse problem is derived by using the Landweber iteration method for the solution of the corresponding conjugate operator equation. In this paper, we also present error estimates between the exact solution and the regularized solution by the a priori and the a posteriori parameter choice rules. Numerical verification on the efficiency and accuracy of the proposed algorithm is performed by solving three numerical examples in one-dimensional and two-dimensional cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Cannon, J.R., Zachmann, D.: Parameter determination in parabolic partial differential equations from overspecified boundary data. Int. J. Eng. Sci. 20(6), 779–788 (1982). https://doi.org/10.1016/0020-7225(82)90087-8

    Article  MathSciNet  MATH  Google Scholar 

  2. Chadan, K., Colton, D., Päivärinta, L., Rundell, W.: An Introduction to Inverse Scattering and Inverse Spectral Problems. SIAM Monographs on Mathematical Modeling and Computation. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (1997). https://doi.org/10.1137/1.9780898719710

    Book  MATH  Google Scholar 

  3. Chen, C.S., Fan, C.M., Wen, P.H.: The method of approximate particular solutions for solving elliptic problems with variable coefficients. Int. J. Comput. Methods 8(3), 545–559 (2011). https://doi.org/10.1142/S0219876211002484

    Article  MathSciNet  MATH  Google Scholar 

  4. Dien, N.M., Trong, D.D.: The backward problem for nonlinear fractional diffusion equation with time-dependent order. Bull. Malays. Math. Sci. Soc. 44(5), 3345–3359 (2021). https://doi.org/10.1007/s40840-021-01113-y

    Article  MathSciNet  MATH  Google Scholar 

  5. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems, Volume 375 of Mathematics and Its Applications. Kluwer Academic Publishers Group, Dordrecht (1996)

    Book  Google Scholar 

  6. Floridia, G., Li, Z.Y., Yamamoto, M.: Well-posedness for the backward problems in time for general time-fractional diffusion equation. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 31(3), 593–610 (2020). https://doi.org/10.4171/rlm/906

    Article  MathSciNet  MATH  Google Scholar 

  7. Floridia, G., Yamamoto, M.: Backward problems in time for fractional diffusion-wave equation. Inverse Probl. 36(12), 125016, 14 (2020). https://doi.org/10.1088/1361-6420/abbc5e

    Article  MathSciNet  MATH  Google Scholar 

  8. Jin, B.T., Rundell, W.: An inverse problem for a one-dimensional time-fractional diffusion problem. Inverse Probl. 28(7), 075010, 19 (2012). https://doi.org/10.1088/0266-611/28/7/075010

    Article  MathSciNet  MATH  Google Scholar 

  9. Johansson, B.T., Lesnic, D.: A variational method for identifying a spacewise-dependent heat source. IMA J. Appl. Math. 72(6), 748–760 (2007). https://doi.org/10.1093/imamat/hxm024

    Article  MathSciNet  MATH  Google Scholar 

  10. Johansson, B.T., Lesnic, D.: A procedure for determining a spacewise dependent heat source and the initial temperature. Appl. Anal. 87(3), 265–276 (2008). https://doi.org/10.1080/00036810701858193

    Article  MathSciNet  MATH  Google Scholar 

  11. Kirsch, A.: An Introduction to the Mathematical Theory of Inverse Problems, Volume 120 of Applied Mathematical Sciences. Springer, New York (1996). https://doi.org/10.1007/978-3-030-63343-1

    Book  Google Scholar 

  12. Lesnic, D., Elliott, L.: The decomposition approach to inverse heat conduction. J. Math. Anal. Appl. 232, 82–98 (1999). https://doi.org/10.1006/jmaa.1998.6243

    Article  MathSciNet  MATH  Google Scholar 

  13. Li, D.F., Liao, H.L., Sun, W.W., Wang, J.L., Zhang, J.W.: Analysis of \(L1\)-Galerkin FEMs for time-fractional nonlinear parabolic problems. Commun. Comput. Phys. 24(1), 86–103 (2018). https://doi.org/10.4208/cicp.OA-2017-0080

    Article  MathSciNet  MATH  Google Scholar 

  14. Li, D.F., Sun, W.W., Wu, C.D.: A novel numerical approach to time-fractional parabolic equations with nonsmooth solutions. Numer. Math. Theory Methods Appl. 14(2), 355–376 (2021). https://doi.org/10.4208/nmtma.OA-2020-0129

    Article  MathSciNet  MATH  Google Scholar 

  15. Li, G.S., Zhang, D., Jia, X.Z., Yamamoto, M.: Simultaneous inversion for the space-dependent diffusion coefficient and the fractional order in the time-fractional diffusion equation. Inverse Probl. 29(6), 065014, 36 (2013). https://doi.org/10.1088/0266-5611/29/6/065014

    Article  MathSciNet  MATH  Google Scholar 

  16. Liu, J.J., Yamamoto, M.: A backward problem for the time-fractional diffusion equation. Appl. Anal. 89(11), 1769–1788 (2010). https://doi.org/10.1080/00036810903479731

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu, J.J., Yamamoto, M., Yan, L.: On the uniqueness and reconstruction for an inverse problem of the fractional diffusion process. Appl. Numer. Math. 87, 1–19 (2015). https://doi.org/10.1016/j.apnum.2014.08.001

    Article  MathSciNet  MATH  Google Scholar 

  18. Liu, J.J., Yamamoto, M., Yan, L.L.: On the reconstruction of unknown time-dependent boundary sources for time fractional diffusion process by distributing measurement. Inverse Probl. 32(1), 015009, 25 (2016). https://doi.org/10.1088/0266-5611/32/1/015009

    Article  MathSciNet  MATH  Google Scholar 

  19. Luc, M., Yamamoto, M.: Coefficient inverse problem for a fractional diffusion equation. Inverse Probl. 29(7), 075013, 8 (2013). https://doi.org/10.1088/0266-5611/29/7/075013

    Article  MathSciNet  MATH  Google Scholar 

  20. Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339(1), 1–77 (2000). https://doi.org/10.1016/S0370-1573(00)00070-3

  21. Metzler, R., Klafter, J.: Subdiffusive transport close to thermal equilibrium: from the Langevin equation to fractional diffusion. Phys. Rev. E 61(6), 6308–6311 (2000). https://doi.org/10.1103/PhysRevE.61.6308

    Article  Google Scholar 

  22. Nabil, S., Fairouz, Z.: A modified Tikhonov regularization method for a class of inverse parabolic problems. An. Ştiinţ. Univ. “Ovidius” Constanţa Ser. Mat. 28(1), 181–204 (2020). https://doi.org/10.2478/auom-2020-0013

  23. Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences, vol. 44. Springer, New York (1983)

    MATH  Google Scholar 

  24. Podlubny, I.: Fractional Differential Equations, Volume 198 of Mathematics in Science and Engineering. Academic Press, Inc., San Diego (1999). An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications

  25. Raberto, M., Scalas, E., Mainardi, F.: Waiting-times and returns in high-frequency financial data: an empirical study. Phys. A Stat. Mech. Appl. 314(1), 749–755 (2002). https://doi.org/10.1016/S0378-4371(02)01048-8

    Article  MATH  Google Scholar 

  26. Ren, C., Xu, X., Lu, S.: Regularization by projection for a backward problem of the time-fractional diffusion equation. J. Inverse Ill Posed Probl. 22(1), 121–139 (2014). https://doi.org/10.1515/jip-2011-0021

    Article  MathSciNet  MATH  Google Scholar 

  27. Ruan, Z.S., Yang, Z.J., Lu, X.L.: Tikhonov regularisation method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation. East Asian J. Appl. Math. 5(3), 273–300 (2015). https://doi.org/10.4208/eajam.310315.030715a

    Article  MathSciNet  MATH  Google Scholar 

  28. Ruan, Z.S., Yang, Z.J., Lu, X.L.: An inverse source problem with sparsity constraint for the time-fractional diffusion equation. Adv. Appl. Math. Mech. 8(1), 1–18 (2016). https://doi.org/10.4208/aamm.2014.m722

    Article  MathSciNet  MATH  Google Scholar 

  29. Ruan, Z.S., Zhang, W., Wang, Z.W.: Simultaneous inversion of the fractional order and the space-dependent source term for the time-fractional diffusion equation. Appl. Math. Comput. 328, 365–379 (2018). https://doi.org/10.1016/j.amc.2018.01.025

    Article  MathSciNet  MATH  Google Scholar 

  30. Rundell, W., Xu, X., Zuo, L.H.: The determination of an unknown boundary condition in a fractional diffusion equation. Appl. Anal. 92(7), 1511–1526 (2013). https://doi.org/10.1080/00036811.2012.686605

    Article  MathSciNet  MATH  Google Scholar 

  31. Wang, J.G., Wei, T.: An iterative method for backward time-fractional diffusion problem. Numer. Methods Partial Differ. Equ. 30(6), 2029–2041 (2014). https://doi.org/10.1002/num.21887

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang, L.Y., Liu, J.J.: Data regularization for a backward time-fractional diffusion problem. Comput. Math. Appl. 64(11), 3613–3626 (2012). https://doi.org/10.1016/j.camwa.2012.10.001

    Article  MathSciNet  MATH  Google Scholar 

  33. Wei, T., Zhang, Z.Q.: Reconstruction of a time-dependent source term in a time-fractional diffusion equation. Eng. Anal. Bound. Elem. 37(1), 23–31 (2013). https://doi.org/10.1016/j.enganabound.2012.08.003

    Article  MathSciNet  MATH  Google Scholar 

  34. Wei, T., Zhang, Z.Q.: Stable numerical solution to a Cauchy problem for a time fractional diffusion equation. Eng. Anal. Bound. Elem. 40, 128–137 (2014). https://doi.org/10.1016/J.ENGANABOUND.2013.12.002

    Article  MathSciNet  MATH  Google Scholar 

  35. Xiong, X.T., Wang, J.X., Li, M.: An optimal method for fractional heat conduction problem backward in time. Appl. Anal. 91(4), 823–840 (2012). https://doi.org/10.1080/00036811.2011.601455

    Article  MathSciNet  MATH  Google Scholar 

  36. Yang, L., Deng, Z.C., Hon, Y.C.: Simultaneous identification of unknown initial temperature and heat source. Dyn. Syst. Appl. 25(4), 583–602 (2016)

    MathSciNet  MATH  Google Scholar 

  37. Yang, F., Ren, Y.P., Li, X.X., Li, D.G.: Landweber iterative method for identifying a space-dependent source for the time-fractional diffusion equation. Bound. Value Probl. 163, 19 (2017). https://doi.org/10.1186/s13661-017-0898-2

    Article  MathSciNet  MATH  Google Scholar 

  38. Yang, F., Zhang, Y., Li, X.X.: Landweber iterative method for identifying the initial value problem of the time-space fractional diffusion-wave equation. Numer. Algorithms 83(4), 1509–1530 (2020). https://doi.org/10.1007/s11075-019-00734-6

    Article  MathSciNet  MATH  Google Scholar 

  39. Yuste, S.B., Acedo, L., Lindenberg, K.: Reaction front in an a + b \(\rightarrow \) c reaction-subdiffusion process. Phys. Rev. E 69(3), 036126 (2004). https://doi.org/10.1103/PhysRevE.69.036126

  40. Yuste, S.B., Lindenberg, K.: Subdiffusion-limited reactions. Chem. Phys. 284(1), 169–180 (2002). Strange Kinetics. https://doi.org/10.1016/S0301-0104(02)00546-3

  41. Zhang, Y., Xu, X.: Inverse source problem for a fractional diffusion equation. Inverse Probl. 27(3), 035010, 12 (2011). https://doi.org/10.1088/0266-5611/27/3/035010

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to express their most sincere thanks to the editor and referees for their very helpful comments and suggestions, which greatly improved the quality of this paper. The work described in this article was supported by the NNSF of China (11326234), NSF of Gansu Province (145RJZA099), Scientific research project of Higher School in Gansu Province (2014A-012), and Project of NWNU-LKQN2020-08.

Author information

Authors and Affiliations

  1. Department of Mathematics, Northwest Normal University, Lanzhou, 730070, People’s Republic of China

    Jin Wen, Zhuan-Xia Liu & Chong-Wang Yue

  2. School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou, 730070, People’s Republic of China

    Shi-Juan Wang

  3. School of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou, 730020, People’s Republic of China

    Shi-Juan Wang

Authors
  1. Jin Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhuan-Xia Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chong-Wang Yue
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shi-Juan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jin Wen.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wen, J., Liu, ZX., Yue, CW. et al. Landweber iteration method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation. J. Appl. Math. Comput. 68, 3219–3250 (2022). https://doi.org/10.1007/s12190-021-01656-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-021-01656-0

Keywords

Mathematics Subject Classification

Search

Navigation