Skip to main content

Advertisement

SpringerLink
Log in

Novel algebraic criteria on global Mittag–Leffler synchronization for FOINNs with the Caputo derivative and delay

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

A Correction to this article was published on 15 December 2021

This article has been updated

Abstract

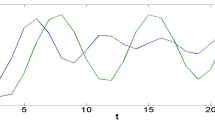
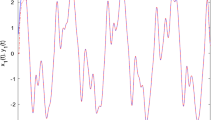
This paper focuses on the global Mittag–Leffler (M–L) synchronization for fractional-order inertial neural networks (FOINNs) including the Caputo derivative and delay. By choosing an appropriate variable transformation, the considered system including the inertial term is transformed into two fractional-order nonlinearly coupled interconnected subsystems. Combining with the delayed-feedback controller, fractional Lyapunov functional approach and inequality analysis technique, multi sets of novel algebraic criteria on the global M–L synchronization between derive-response systems are established. The main prominent highlight of this paper is that the proposed results are characterized by the algebraic inequalities form, which can simplify the calculation and facilitate the test. Two numerical simulation examples validate the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Change history

References

  1. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  2. Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)

    MATH  Google Scholar 

  3. Loghman, E., Bakhtiari-Nejad, F., Kamali, E.A., Abbaszadeh, M., Amabili, M.: Nonlinear vibration of fractional viscoelastic micro-beams. Int. J. Non Linear Mech. 137, 103811 (2021). https://doi.org/10.1016/j.ijnonlinmec.2021.103811

    Article  MATH  Google Scholar 

  4. Tarasov, V.E.: Fractional econophysics: market price dynamics with memory effects. Physica A 557, 124865 (2020). https://doi.org/10.1016/j.physa.2020.124865

    Article  MathSciNet  MATH  Google Scholar 

  5. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific Press, Singapore (2000)

    Book  Google Scholar 

  6. Yan, X., Zhang, Y., Wei, T.: Identify the fractional order and diffusion coefficient in a fractional diffusion wave equation. Comput. Appl. Math. 393, 113497 (2021). https://doi.org/10.1016/j.cam.2021.113497

    Article  MathSciNet  MATH  Google Scholar 

  7. Baleanu, D., Machado, J.A.T., Luo, A.C.J.: Fractional Dynamics and Control. Springer, New York (2012)

    Book  Google Scholar 

  8. Al-NassirM, S.: Dynamic analysis of a harvested fractional-order biological system with its discretization. Chaos Solitons Fract. 152, 111308 (2021). https://doi.org/10.1016/j.chaos.2021.111308

    Article  MathSciNet  MATH  Google Scholar 

  9. Syed Ali, M., Narayanan, G., Saroha, S., Priya, B., Thakur, G.K.: Finite-time stability analysis of fractional-order memristive fuzzy cellular neural networks with time delay and leakage term. Math. Comput. Simul. 185, 468–485 (2021). https://doi.org/10.1016/j.matcom.2020.12.035

    Article  MathSciNet  MATH  Google Scholar 

  10. Yang, Z., Zhang, J., Niu, Y.: Finite-time stability of fractional-order bidirectional associative memory neural networks with mixed time-varying delays. Appl. Math. Comput. 63, 501–522 (2020). https://doi.org/10.1007/s12190-020-01327-6

    Article  MathSciNet  MATH  Google Scholar 

  11. Ma, K., Sun, S.: Finite-time stability of linear fractional time-delay \(q\)-difference dynamical system. Appl. Math. Comput. 57, 591–604 (2018). https://doi.org/10.1007/s12190-017-1123-2

    Article  MathSciNet  MATH  Google Scholar 

  12. Syed Ali, M., Narayanan, G., Shekher, V., Alsaedi, A., Ahmad, B.: Global Mittag–Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 183, 105088 (2020). https://doi.org/10.1016/j.cnsns.2019.105088

    Article  MathSciNet  MATH  Google Scholar 

  13. Ke, L.: Mittag–Leffler stability and asymptotic \(\omega \)-periodicity of fractional-order inertial neural networks with time-delays. Neurocomputing 465, 53–62 (2021). https://doi.org/10.1016/j.neucom.2021.08.121

    Article  Google Scholar 

  14. Sriraman, R., Cao, Y., Samidurai, R.: Global asymptotic stability of stochastic complex-valued neural networks with probabilistic time-varying delays. Math. Comput. Simul. 171, 103–118 (2020). https://doi.org/10.1016/j.matcom.2019.04.001

    Article  MathSciNet  MATH  Google Scholar 

  15. Gu, Y., Wang, H., Yu, Y.: Stability and synchronization for Riemann–Liouville fractional-order time-delayed inertial neural networks. Neurocomputing 340, 270–280 (2019). https://doi.org/10.1016/j.neucom.2019.03.005

    Article  Google Scholar 

  16. Pahnehkolaei, S.M.A., Alfi, A., Tenreiro Machado, J.A.: Delay independent robust stability analysis of delayed fractional quaternion-valued leaky integrator echo state neural networks with QUAD condition. Appl. Math. Comput. 359, 278–293 (2019). https://doi.org/10.1016/j.amc.2019.04.083

  17. Li, H., Kao, Y., Hu, C., Jiang, H., Jiang, Y.: Robust exponential stability of fractional-order coupled quaternion-valued neural networks with parametric uncertainties and impulsive effects. Chaos Solitons Fract. 143, 110598 (2021). https://doi.org/10.1016/j.chaos.2020.110598

    Article  MathSciNet  MATH  Google Scholar 

  18. Wei, X., Zhang, Z., Lin, C., Chen, J.: Synchronization and anti-synchronization for complex-valued inertial neural networks with time-varying delays. Appl. Math. Comput. 403, 126194 (2021). https://doi.org/10.1016/j.amc.2021.126194

    Article  MathSciNet  MATH  Google Scholar 

  19. Miao, P., Shen, Y., Li, Y., Bao, L.: Finite-time recurrent neural networks for solving nonlinear optimization problems and their application. Neurocomputing 177, 120–129 (2016). https://doi.org/10.1016/j.neucom.2015.11.014

    Article  Google Scholar 

  20. Rakkiyappan, R., Li, X., O’Regan, D.: Dynamics of fuzzy impulsive bidirectional associative memory neural networks with time-varying delays. J. Appl. Math. Comput. 40, 289–317 (2012). https://doi.org/10.1007/s12190-012-0554-z

  21. Liu, W., Huang, J., Yao, Q.: Stability analysis for quaternion-valued inertial memristor-based neural networks with time delays. Neurocomputing 448, 67–81 (2021). https://doi.org/10.1016/j.neucom.2021.03.106

    Article  Google Scholar 

  22. Wei, F., Chen, G., Wang, W.: Finite-time stabilization of memristor-based inertial neural networks with time-varying delays combined with interval matrix method. Knowl. Based Syst. 230, 107395 (2021). https://doi.org/10.1016/j.knosys.2021.107395

    Article  Google Scholar 

  23. Tang, Q., Jian, J.: Global exponential convergence for impulsive inertial complex-valued neural networks with time-varying delays. Math. Comput. Simul. 159, 39–56 (2019). https://doi.org/10.1016/j.matcom.2018.10.009

    Article  MathSciNet  MATH  Google Scholar 

  24. Qiu, J., Yang, X., Cao, J.: Pth moment exponential stochastic synchronization of coupled memristor-based neural networks with mixed delays via delayed impulsive control. Neural Net. Off. J. Int. Neural Netw. Soc. 65, 80–91 (2015). https://doi.org/10.1016/j.neunet.2015.01.008

  25. Feng, Y., Yang, X., Qiang, S., Cao, J.: Synchronization of memristive neural networks with mixed delays via quantized intermittent control. Appl. Math. Comput. 339, 874–887 (2018). https://doi.org/10.1016/j.amc.2018.08.009

    Article  MathSciNet  MATH  Google Scholar 

  26. Babcock, K.L., Westervelt, R.M.: Stability and dynamics of simple electronic neural networks with added inertia. Physica D 23, 464–469 (1986). https://doi.org/10.1016/0167-2789(86)90152-1

    Article  Google Scholar 

  27. Stamova, I.: Global Mittag–Leffler stability and synchronization of impulsive fractional-order neural networks with time-varying delays. Nonlinear Dyn. 77, 1251–1260 (2014). https://doi.org/10.1007/s11071-014-1375-4

    Article  MathSciNet  MATH  Google Scholar 

  28. Vadivel, R., Hammachukiattikul, P., Rajchakit, G., Syed, Ali M., Unyong, B.: Finite-time event-triggered approach for recurrent neural networks with leakage term and its application. Math. Comput. Simul. 182, 765–790 (2021). https://doi.org/10.1016/j.matcom.2020.12.001

  29. Li, H., Jiang, H., Cao, J.: Global synchronization of fractional-order quaternion-valued neural networks with leakage and discrete delays. Neurocomputing 385, 211–219 (2020). https://doi.org/10.1016/j.neucom.2019.12.018

    Article  Google Scholar 

  30. Zhang, H., Cheng, J., Zhang, H.M., Zhang, W., Cao, J.: Quasi-uniform synchronization of Caputo type fractional neural networks with leakage and discrete delays. Chaos Solitons Fract. 152, 111432 (2021). https://doi.org/10.1016/j.chaos.2021.111432

    Article  MathSciNet  MATH  Google Scholar 

  31. Du, F., Lu, J.: New approach to finite-time stability for fractional-order BAM neural networks with discrete and distributed delays. Chaos Solitons Fract. 151, 111225 (2021). https://doi.org/10.1016/j.chaos.2021.111225

    Article  MathSciNet  MATH  Google Scholar 

  32. Zhang, Y., Liu, S., Yang, R., Tan, Y., Li, X.: Global synchronization of fractional coupled networks with discrete and distributed delays. Physica A 514, 830–837 (2019). https://doi.org/10.1016/j.physa.2018.09.129

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang, C., Zhang, H., Zhang, H.M., Zhang, W.: Globally projective synchronization for Caputo fractional quaternion-valued neural networks with discrete and distributed delays. AIMS Math. 6(12), 14000–14012 (2021). https://doi.org/10.3934/math.2021809

    Article  MathSciNet  MATH  Google Scholar 

  34. Zhang, L., Zhong, J., Lu, J.: Intermittent control for finite-time synchronization of fractional-order complex networks. Neural Netw. 144, 11–20 (2021). https://doi.org/10.1016/j.neunet.2021.08.004

    Article  Google Scholar 

  35. Li, L., Liu, X., Tang, M., Zhang, S.: Asymptotical synchronization analysis of fractional-order complex neural networks with non-delayed and delayed couplings. Neural Netw. 445, 180–193 (2021). https://doi.org/10.1016/j.neucom.2021.03.001

    Article  Google Scholar 

  36. Syed Ali, M., Hymavathi, M., Senan, S., Shekher, V., Arik, S.: Global asymptotic synchronization of impulsive fractional-order complex-valued memristor-based neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 78, 104869 (2019). https://doi.org/10.1016/j.cnsns.2019.104869

    Article  MathSciNet  MATH  Google Scholar 

  37. Hu, T., Zhang, X., Zhong, S.: Global asymptotic synchronization of nonidentical fractional-order neural networks. Neurocomputing 313, 39–46 (2018). https://doi.org/10.1016/j.neucom.2018.05.098

    Article  Google Scholar 

  38. Ye, R., Liu, X., Zhang, H., Cao, J.: Global Mittag–Leffler synchronization for fractional-order BAM neural networks with impulses and multiple variable delays via delayed-feedback control strategy. Neural Process. Lett. 49, 1–18 (2019). https://doi.org/10.1007/s11063-018-9801-0

    Article  Google Scholar 

  39. Pratap, A., Raja, R., Sowmiya, C., Bagdasar, O., Cao, J., Rajchakit, G.: Robust generalized Mittag–Leffler synchronization of fractional order neural networks with discontinuous activation and impulses. Neural Process. Lett. 103, 128–141 (2018). https://doi.org/10.1016/j.neunet.2018.03.012

    Article  MATH  Google Scholar 

  40. Chen, J., Li, C., Yang, X.: Global Mittag–Leffler projective synchronization of nonidentical fractional-order neural networks with delay via sliding mode control. Neurocomputing 313, 324–332 (2018). https://doi.org/10.1016/j.neucom.2018.06.029

    Article  Google Scholar 

  41. Xiao, J., Zhong, S., Wen, S.: Improved approach to the problem of the global Mittag–Leffler synchronization for fractional-order multidimension-valued BAM neural networks based on new inequalities. Neural Netw. 133, 87–100 (2021). https://doi.org/10.1016/j.neunet.2020.10.008

    Article  MATH  Google Scholar 

  42. Zhang, W., Sha, C., Cao, J., Wang, G., Wang, Y.: Adaptive quaternion projective synchronization of fractional order delayed neural networks in quaternion field. Appl. Math. Comput. 400, 126045 (2021). https://doi.org/10.1016/j.amc.2021.126045

    Article  MathSciNet  MATH  Google Scholar 

  43. Yang, S., Hu, C., Yu, J., Jiang, H.: Projective synchronization in finite-time for fully quaternion-valued memristive networks with fractional-order. Chaos Solitons Fract. 147, 110911 (2021). https://doi.org/10.1016/j.chaos.2021.110911

    Article  MathSciNet  MATH  Google Scholar 

  44. Chen, J., Zeng, Z., Jiang, P.: Global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 51, 1–8 (2014). https://doi.org/10.1016/j.neunet.2013.11.016

    Article  MATH  Google Scholar 

  45. Li, H., Hu, C., Zhang, L., Jiang, H., Cao, J.: Non-separation method-based robust finite-time synchronization of uncertain fractional-order quaternion-valued neural networks. Appl. Math. Comput. 409, 126377 (2021). https://doi.org/10.1016/j.amc.2021.126377

    Article  MathSciNet  MATH  Google Scholar 

  46. Tang, R., Su, H., Zou, Y., Yang, X.: Finite-time synchronization of Markovian coupled neural networks with delays via intermittent quantized control: linear programming approach. IEEE Trans. Neural Netw. Learn. Syst. (2021). https://doi.org/10.1109/TNNLS.2021.3069926

  47. Yang, X., Li, X., Lu, J., Cheng, Z.: Synchronization of time-delayed complex networks with switching topology via hybrid actuator fault and impulsive effects control. Neurocomputing 50, 4043–4052 (2020). https://doi.org/10.1109/TCYB.2019.2938217

    Article  Google Scholar 

  48. Yang, X., Li, X., Lu, J., Rutkowski, L.: Synchronization of coupled time-delay neural networks with mode-dependent average dwell time switching. Neurocomputing 31, 5483–5496 (2020). https://doi.org/10.1109/TNNLS.2020.2968342

    Article  MathSciNet  Google Scholar 

  49. Yang, X., Feng, Z., Feng, J., Cao, J.: Synchronization of discrete-time neural networks with delays and Markov jump topologies based on tracker information. Neural Netw. 85, 157–164 (2017). https://doi.org/10.1016/j.neunet.2016.10.006

    Article  MATH  Google Scholar 

  50. Yang, X., Lu, J., Ho, D., Song, Q.: Synchronization of uncertain hybrid switching and impulsive complex networks. Appl. Math. Model. 59, 379–392 (2018). https://doi.org/10.1016/j.apm.2018.01.046

    Article  MathSciNet  MATH  Google Scholar 

  51. Yang, X., Wan, X., Cheng, Z., Cao, J., Rutkowski, L.: Synchronization of switched discrete-time neural networks via quantized output control with actuator fault. IEEE Trans. Neural Netw. Learn. Syst. 32, 4191–4201 (2021). https://doi.org/10.1109/TNNLS.2020.3017171

    Article  MathSciNet  Google Scholar 

  52. Duarte-Mermoud, M.A., Aguila-Camacho, N., Gallegos, J.A., Castro-Linares, R.: Using general quadratic Lyapunov functions to prove Lyapunovuniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 22, 650–659 (2015). https://doi.org/10.1016/j.cnsns.2014.10.008

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported the Natural Science Foundation of Anhui Province of China (No. 1908085MA01), the Natural Science Foundation of the Higher Education Institutions of Anhui Province (Nos. KJ2019A0557, KJ2019A0573) and the Top Young Talents Program of Higher Learning Institutions of Anhui Province (No. gxyq2019048).

Author information

Authors and Affiliations

  1. School of Mathematics and Physics, Anqing Normal University, Anqing, 246133, People’s Republic of China

    Yuhong Cheng, Hai Zhang, Weiwei Zhang & Hongmei Zhang

  2. College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing, 211106, People’s Republic of China

    Weiwei Zhang

Authors
  1. Yuhong Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hai Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weiwei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hongmei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hai Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, Y., Zhang, H., Zhang, W. et al. Novel algebraic criteria on global Mittag–Leffler synchronization for FOINNs with the Caputo derivative and delay. J. Appl. Math. Comput. 68, 3527–3544 (2022). https://doi.org/10.1007/s12190-021-01672-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-021-01672-0

Keywords

Mathematics Subject Classification

Search

Navigation