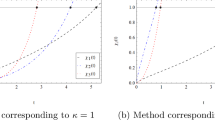
Abstract
The purpose of this paper is to study a semilocal convergence result for the King-Werner iterative method in Banach space setting under a gamma-type condition. The convergence of the method is established under weaker conditions than those used in previous works; we only use hypotheses up to the second Fréchet derivative of the involved operator. In addition, we illustrate the applicability of our result with some numerical examples.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Kantorovich, L.V.: On Newton’ s method for functional equations. In Doklady Akademii Nauk SSSR 59, 1237–1240 (1948)
Amat, S., Busquier, S., Gutiérrez, J.M.: Third-order iterative methods with applications to Hammerstein equations: A unified approach. J. Comput. Appl. Math. 235(9), 2936–2943 (2011)
Argyros, I.K.: Chebysheff-Halley-like methods in Banach spaces. Korean J. Comput. Appl. Math. 4(1), 83 (1997)
Chen, D., Argyros, I.K.: The midpoint method for solving nonlinear operator equations in Banach space. Appl. Math. Lett. 5(4), 7–9 (1992)
Ostrowski, A.M.: Solution of Equations in Euclidean and Banach Spaces. Academic Press, Pure and applied mathematics (1973)
Traub, J.F.: Iterative Methods for the Solution of Equations, vol. 312. American Mathematical Society, Providence (1982)
Argyros, I.K.: Computational Theory of Iterative Methods, vol. 15. Elsevier Science, San Diego, CA, USA (2007)
Ezquerro, J.A., Hernández, M.A.: The Classic Theory of Kantorovich, pp. 1–38. Springer International Publishing, Cham (2017)
Werner, W.: Über ein verfahren der ordnung \(1 + \sqrt{2} \) zur nullstellenbestimmung. Numer. Math. 32(3), 333–342 (1979)
Werner, W.: Some supplementary results on the 1+ \(\sqrt{2} \) order method for the solution of nonlinear equations. Numer. Math. 38(3), 383–392 (1982)
King, R.F.: Tangent methods for nonlinear equations. Numer. Math. 18(4), 298–304 (1971)
Ostrowski, A.M.: Solution of Equations and Systems of Equations. Academic Press, New York (1966)
Argyros, I.K., Ren, H.: On the convergence of efficient King-Werner-type methods of order \(1+\sqrt{2}\). J. Comput. Appl. Math. 285, 169–180 (2015)
Cárdenas, E., Castro, R., Sierra, W.: A Newton-type midpoint method with high efficiency index. J. Math. Anal. Appl. 491(2), 124381 (2020)
Han, D.F., Wang, X.H.: Convergence on a deformed Newton method. Appl. Math. Comput. 94(1), 65–72 (1998)
McDougall, T.J., Wotherspoon, S.J.: A simple modification of Newton’s method to achieve convergence of order 1+\(\sqrt{2}\). Appl. Math. Lett. 29, 20–25 (2014)
Ren, H.: On the local convergence of a deformed Newton’s method under Argyros-type condition. J. Math. Anal. Appl. 321(1), 396–404 (2006)
Wang, X.H., Han, D.F., Sun, F.Y.: Point estimates on deformed Newton’s iteration. Math. Numer. Sinica 12, 145–156 (1990)
Wang, X.H., Shiming, Z.: On the convergence of King-Werner’s iteration procedure for solving nonliear equations. Math. Numer. Sinica 4, 70–79 (1982)
Zhao, Y., Wu, Q.: Convergence analysis for a deformed Newton’s method with third-order in Banach space under \(\gamma \)-condition. Int. J. Comput. Math. 86(3), 441–450 (2009)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first and the third author wish to thank the Universidad del Cauca for supporting this work through research project VRI ID 5464.
Rights and permissions
About this article
Cite this article
Cárdenas, E., Castro, R. & Sierra, W. Convergence analysis for the King-Werner method under \(\gamma -\)conditions. J. Appl. Math. Comput. 68, 4605–4620 (2022). https://doi.org/10.1007/s12190-022-01720-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-022-01720-3