Abstract
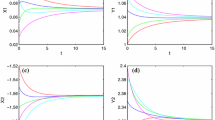
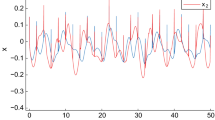
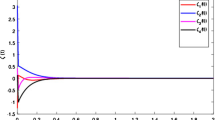
This paper focuses on the global asymptotic stability of fractional-order complex-valued fuzzy cellular neural networks (CVFCNNs) with impulse effects and time-varying delays. In this paper, the new Lyapunov–Krasovskii functional is designed to derive the global asymptotic stability criterion for the CVFCNNs by employing the fractional Barbalat’s lemma and some inequality techniques. In order to derive the existence and uniqueness for considered fractional-order systems, the contraction mapping principle is used to obtain the constraints. A numerical example is carried out to validate the efficacy of the proposed method and fractional-order derivatives.








Similar content being viewed by others
References
Sakthivel, R., Sakthivel, R., Kwon, O., Sakthivel, P., Marshal Anthoni, S.: Observer-based robust synchronization of fractional-order multi-weighted complex dynamical networks. Nonlinear Dyn. 98, 1231–1249 (2019)
Yang, Z., Zheng, J., Niu, Y.: Finite-time stability of fractional-order bidirectional associative memory neural networks with mixed time-varying delays. J. Comput. Appl. Math. 63, 501–522 (2020)
Ali, M.S., Narayanan, G., Orman, Z., Shekher, V., Arik, S.: Finite time stability analysis of fractional-order complex-valued memristive neural networks with proportional delays. Neural Process. Lett. 51, 407–426 (2020)
Rajivganthi, C., Rihan, F.A., Lakshmanan, S., Muthukumar, P.: Finite-time stability analysis for fractional-order Cohen–Grossberg BAM neural networks with time delays. Neural Comput. Appl. 29, 1309–1320 (2018)
Yang, T., Yang, L.B.: The global stability of fuzzy cellular neural network. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 43, 880–883 (1996)
Rajchaikit, G., Saravanakumar, R.: Exponential stability of semi-Markovian jump generalized neural networks with interval time-varying delays. Neural Comput. Appl. 29, 483–492 (2018)
Aouiti, C., Sakthivel, R., Aouiti, F.: Global dissipativity of fuzzy cellular neural networks with inertial term and proportional delays. Int. J. Syst. Sci. 51, 1392–1405 (2020)
Ratnavelu, K., Manikandan, M., Balasubramaniam, P.: Design of state estimator for BAM fuzzy cellular neural networks with leakage and unbounded distributed delays. Inf. Sci. 397, 91–99 (2017)
Liu, P.: The fuzzy associative memory of max–min fuzzy neural network with threshold. Fuzzy Set. Syst. 107, 147–157 (1999)
Rajchaikit, G.: Delay-dependent stability of cellular neural networks with multiple delays. Appl. Mech. Mater. 598, 718–722 (2014)
Stamova, I., Stamov, T., Li, X.: Global exponential stability of a class of impulsive cellular neural networks with supremums. Int. J. Adapt. Control 28, 1227–1239 (2014)
Long, S., Xu, D.: Stability analysis of stochastic fuzzy cellular neural networks with time-varying delays. Neurocomputing 74, 2385–2391 (2011)
Arena, P., Caponetto, R., Fortuna, L., Porto, D.: Bifurcation and chaos in noninteger order cellular neural networks. Int. J. Bifurc. Chaos 8, 1527–1539 (1998)
Zheng, M., Li, L., Peng, H., Xiao, J., Yang, Y., Zhang, Y., Zhao, H.: Finite-time stability and synchronization of memristor-based fractional-order fuzzy cellular neural networks. Commun. Nonlinear Sci. 58, 272–291 (2018)
Stamova, I., Simeonov, S.: Delayed reaction-diffusion cellular neural networks of fractional order: Mittag–Leffler stability and synchronization. J. Comput. Nonlinear Dyn. 13, 011015 (2018)
Ali, M.S., Narayanan, G., Saroha, S., Priya, B., Thakur, G.K.: Finite-time stability analysis of fractional-order memristive fuzzy cellular neural networks with time delay and leakage term. Math. Comput Simul. 185, 468–485 (2021)
Qu, H., Zhang, T., Zhou, J.: Global stability analysis of S-asymptotically \(\omega \)-periodic oscillation in fractional-order cellular neural networks with time variable delays. Neurocomputing 399, 390–398 (2020)
Xu, X., Liao, M., Li, P., Liu, Z., Yuan, S.: New results on pseudo almost periodic solutions of quaternion-valued fuzzy cellular neural networks with delays. Fuzzy Set. Syst. 411, 25–47 (2020)
Xu, C.: On pseudo almost automorphic solutions to quaternion-valued cellular neural networks with delays. IEEE Access 7, 6927–6936 (2020)
Ali, M.S., Hymavathi, M.: Synchronization of fractional order neutral type fuzzy cellular neural networks with discrete and distributed delays via state feedback control. Neural Process. Lett. 53, 929–957 (2021)
Arik, S.: A modified Lyapunov functional with application to stability of neutral-type neural networks with time delays. J. Frankl. Inst. 356, 276–291 (2019)
Sakthivel, R., Sakthivel, R., Kwon, O.M., Kaviarasan: Fault estimation and synchronization control for complex dynamical networks with time-varying coupling delay. Int. J. Robust Nonlinear Control. 31, 2205–2221 (2021)
Datta, R., Saravanakumar, R., Dey, R., Bhattacharya, B., Ahn, C.K.: Improved stabilization criteria for Takagi–Sugeno fuzzy systems with variable delays. Inf. Sci. 579, 591–606 (2021)
He, X., Li, X., Nieto, J.J.: Finite-time stability and stabilization for time-varying systems. Chaos Solitons Fractals 148, 111076 (2021)
Stamov, G., Stamova, I.: Impulsive fractional-order neural networks with time-varying delays: almost periodic solutions. Neural Comput. Appl. 28, 3307–3316 (2017)
Thi, N., Sau, N.H., Thuan, M.V.: LMI conditions for fractional exponential stability and passivity analysis of uncertain Hopfield conformable fractional-order neural networks. Neural Process. Lett. (2022). https://doi.org/10.1007/s11063-021-10683-8
Zhang, X., Zhang, X., Li, D., Ynag, D.: Adaptive synchronization for a class of fractional order time-delay uncertain chaotic systems via fuzzy fractional order neural network. Int. J. Control Autom. Syst. 17, 1209–1220 (2019)
Stamov, G., Stamova, I., Simeonov, S.: Almost periodicity in impulsive fractional-order reaction–diffusion neural networks with time-varying delays. IEEE Trans Cybern. 51, 151–161 (2021)
Stamova, I., Henderson, J.: Practical stability analysis of fractional-order impulsive control systems. ISA Trans. 64, 77–85 (2016)
Sunaga, Y., Natsuaki, R., Hirose, A.: Land form classification and similar land-shape discovery by using complex-valued convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 57, 7907–7917 (2019)
Jian, J., Wan, P.: Lagrange \(\alpha \)-exponential stability and \(\alpha \)-exponential convergence for fractional-order complex-valued neural networks. Neural Netw. 91, 1–10 (2019)
Li, H., Kao, Y., Li, H.L.: Globally \(\beta \)-Mittag–Leffler stability and Mittag–Leffler convergence in Lagrange sense for impulsive fractional-order complex-valued neural networks. Chaos Solitons Fractals 148, 111061 (2021)
Wan, P., Jian: Impulsive stabilization and synchronization of fractional-order complex-valued neural networks. Neural Process Lett. 50, 2201–2218 (2019)
Ali, M.S., Narayanan, G., Shekher, V., Alsaedi, A., Ahamed, B.: Global Mittag–Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays. Commun. Nonlinear Sci. 83, 105088 (2020)
Zheng, B., Yu, J., Jiang, H.: Finite-time synchronization of fully complex-valued neural networks with fractional-order. Neurocomputing 373, 70–80 (2020)
Chen, Y., Song, Q., Zhao, Z., Liu, Y., Alsaudi, F.: Global Mittag–Leffler stability for fractional-order quaternion-valued neural networks with piecewise constant arguments and impulses. Int. J. Syst. Sci. (2021). https://doi.org/10.1080/00207721.2021.2023688
Wang, Z., Wang, X., Li, Y., Huang, X.: Stability and Hopf bifurcation of fractional-order complex-valued single neuron model with time delay. Int. J. Bifurc. Chaos. 27, 1750209 (2017)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Yang, T., Yang, L.B., Wu, C.W., Chua, L.O.: Fuzzy cellular neural networks: theory. In: Proceedings of IEEE International Workshop on Cellular Neural Networks and Applications, vol. 1, pp. 1–6 (1996)
Chen, B., Chen, J.: Razumikhin-type stability theorems for functional fractional-order differential systems and applications. Appl. Math. Comput. 254, 63–69 (2015)
Arik, S.: An analysis of global asymptotic stability of delayed cellular neural networks. IEEE Trans. Neural Netw. 13, 1239–1242 (2002)
Long, S., Song, Q., Wang, X., Li, D.: Stability analysis of fuzzy cellular neural networks with time delay in the leakage term and impulsive perturbations. J. Frankl. Inst. 349, 2461–2479 (2012)
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Aravind, R.V., Balasubramaniam, P. Global asymptotic stability of delayed fractional-order complex-valued fuzzy cellular neural networks with impulsive disturbances. J. Appl. Math. Comput. 68, 4713–4731 (2022). https://doi.org/10.1007/s12190-022-01726-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-022-01726-x
Keywords
- Fractional-order systems
- Complex-valued fuzzy cellular neural networks
- Impulsive disturbances
- Time delays
- Global asymptotic stability