Skip to main content
Springer Nature Link
Log in

Two spectral conjugate gradient methods for unconstrained optimization problems

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

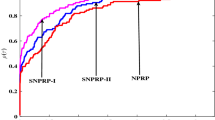
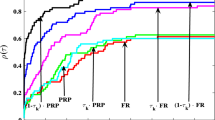
Abstract

Two new spectral conjugate gradient methods (ZL1 method and ZL2 method) for solving unconstrained optimization problems are established. Under the standard Wolfe line search, the search direction generated by the ZL1 method is a descent direction. The search direction of the ZL2 method satisfies descent property independent of the line search. The global convergence of the two new methods can be demonstrated under the standard Wolfe line search. Numerical experiments are presented to show that the two methods are effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Hestenes, M.R., Stiefel, E.: Method of conjugate gradient for solving linear equations. J. Res. Natl. Bureau Stand. 49, 409–436 (1952)

    Article  MATH  Google Scholar 

  2. Fletcher, R., Reeves, C.M.: Function minimization by conjugate gradients. Comput. J. 7, 149–154 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  3. Polak, E., Ribiere, G.: Note sur la convergence de méthodes de directions conjugées. Rev. Française Inf. Rech. Oper. 3, 35–43 (1969)

    MATH  Google Scholar 

  4. Polyak, B.T.: The conjugate gradient method in extreme problems. USSR. Comput. Math. Math. Phys. 9, 94–112 (1969)

    Article  MATH  Google Scholar 

  5. Fletcher, R.: Practical method of optimization, vol I unconstrained optimization. Wiley, NewYork (1987)

  6. Liu, Y., Storey, C.: Efficient generalized conjugate gradient algorithms, part I theory. J. Optim. Theory Appl. 69, 129–137 (1991)

  7. Dai, Y.H., Yuan, Y.: A three-parameter family of nonlinear conjugate gradient methods. Math. Comp. 70, 1155–1167 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  8. Zhang, L., Zhou, W.J., Li, D.H.: Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search. Numer. Math. 104, 561–572 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhang, L., Zhou, W.J., Li, D.H.: A descent modified Polak-Ribière-Polyak conjugate gradient method and its global convergence. IMA J. Numer. Anal. 26, 629–640 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Andrei, N.: New accelerated conjugate gradient algorithms as a modification of Dai-Yuans computational scheme for unconstrained optimization. J. Comput. Appl. Math. 234, 3397–3410 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Sun, M., Liu, J.: Three modified Polak-Ribiere-Polyak conjugate gradient methods with sufficient descent property. IMA J. Numer. Anal. 2015, 125–129 (2015)

    MATH  Google Scholar 

  12. Jiang, X.Z., Jian, J.B.: Improved Fletcher-Reeves and Dai-Yuan conjugate gradient methods with the strong Wolfe line search. J. Comput. Appl. Math. 348, 525–534 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  13. Dong, X.L.: A modified nonlinear Polak-Ribière-Polyak conjugate gradient method with sufficient descent property. Calcolo. 57, 1–14 (2020)

    Article  MATH  Google Scholar 

  14. Zhu, Z.B., Zhang, D.D., Wang, S.: Two modified DY conjugate gradient methods for unconstrained optimization problems. Appl. Math. Comput. 373, 1–10 (2020)

    MathSciNet  MATH  Google Scholar 

  15. Birgin, E.G., Martínez, J.M.: A spectral conjugate gradient method for unconstrained optimization. Appl. Math. Optim. 43, 117–128 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  16. Awwal, A.M., Sulaiman, I.M., Malik, M., et al.: A spectral RMIL+ conjugate gradient method for unconstrained optimization with applications in portfolio selection and motion control. IEEE Access. 9, 75398–75414 (2021)

    Article  Google Scholar 

  17. Aji, S., Kumam, P., Awwal, A.M., et al.: An efficient DY-type spectral conjugate gradient method for system of nonlinear monotone equations with application in signal recovery. Aims Math. 6(8), 8078–8106 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hu, P., Du, X.W., Guo, C.F.: Global convergence of a modified LS spectral conjugate gradient method. J. Chongqing Normal Univ. (Nat. Sci.) 29, 13–15 (2012)

    MATH  Google Scholar 

  19. Lin, S.H.: Global convergence of two spectral conjugate gradient methods for unconstrained optimization. J. Chongqing Normal Univ. (Nat. Sci.) 32, 1–6 (2015)

    Google Scholar 

  20. Xia, L.N., Zhu, Z.B.: Two modified FR spectral conjugate gradient methods under wolfe line search. Math. Appl. 34, 647–656 (2021)

    MATH  Google Scholar 

  21. Andrei, N.: An unconstrained optimization test functions collection. Adv. Model. Optim. 10, 147–161 (2008)

    MathSciNet  MATH  Google Scholar 

  22. Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91, 201–213 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Computing Science Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology, Guilin, 541004, China

    Zhibin Zhu, Ai Long & Tian Wang

Authors
  1. Zhibin Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ai Long
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Tian Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ai Long.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work is supported by the National Natural Science Foundation of China (61967004, 11901137), Guangxi Key Laboratory of Cryptography and Information Security (GCIS201927, GCIS201621) and Guangxi Key Laboratory of Automatic Detecting Technology and Instruments (YQ20113, YQ20114)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhu, Z., Long, A. & Wang, T. Two spectral conjugate gradient methods for unconstrained optimization problems. J. Appl. Math. Comput. 68, 4821–4841 (2022). https://doi.org/10.1007/s12190-022-01730-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01730-1

Keywords