Skip to main content

Advertisement

Springer Nature Link
Log in

Threshold dynamics and optimal control of a dengue epidemic model with time delay and saturated incidence

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

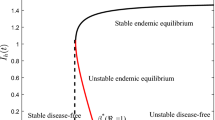
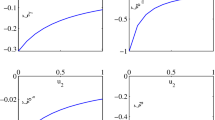
In this paper, an epidemic model of dengue fever with time delay and saturated incidence rate is studied. The basic reproduction number is calculated by the next-generation matrix method. The local stability of each of feasible equilibria is obtained by analyzing the corresponding characteristic equations. Lyapunov functional method and LaSalle’s invariance principle are used to prove that the disease-free equilibrium is globally asymptotically stable when the basic reproduction number is less than 1; when the basic reproduction number is greater than 1, the endemic equilibrium is globally asymptotically stable. Further, optimal control strategy for the prevention and control of dengue fever infection is suggested based on Pontryagin’s minimum principle with delay. In addition, sensitivity analysis is carried out on basic reproduction number and numerical simulation of the dengue outbreak in Guangdong, in 2014, is given to illustrate the rationality of the model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Achee, N.L., Gould, F., Perkins, T.A., et al.: A critical assessment of vector control for dengue prevention. PLoS Neglect. Trop. D. 9(5), 1–19 (2015)

    Article  Google Scholar 

  2. Beretta, E., Kuang, Y.: Geometric stability switch criteria in delay differential systems with delay dependent parameters. Siam J. Math. Anal. 33, 1144–1165 (2002)

    Article  MATH  Google Scholar 

  3. Cai, L., Guo, S., Li, X., et al.: Global dynamics of a dengue epidemic mathematical model. Chaos Solitons & Fractal. 42(4), 2297–2304 (2009)

    Article  MATH  Google Scholar 

  4. Cai, L., Li, X.: Global analysis of a vector-host epidemic model with nonlinear incidences. Appl. Math. Comput. 217(7), 3531–3541 (2010)

    MATH  Google Scholar 

  5. Cai, L., Li, X., Fang, B., et al.: Global properties of vector-host disease models with time delays. J. Math. Biol. 74(6), 1397–1423 (2017)

    Article  MATH  Google Scholar 

  6. Capasso, V., Serio, G.: A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 42(1–2), 43–61 (1978)

    Article  MATH  Google Scholar 

  7. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)

    Article  MATH  Google Scholar 

  8. Ding, D., Wang, X., Ding, X.: Global stability of multigroup dengue disease transmission model. J. Appl. Math. 2012(3), 1–11 (2012)

    MATH  Google Scholar 

  9. Esteva, L., Vargas, C.: Analysis of a dengue disease transmission model. Math. Biosci. 150(2), 131–151 (1998)

    Article  MATH  Google Scholar 

  10. Esteva, L., Vargas, C.: A model for dengue disease with variable human population. J. Math. Biol. 38(3), 220–240 (1999)

    Article  MATH  Google Scholar 

  11. Fleming, W.H., Rishel, R.W.: Deterministic and Stochastic Optimal Control. Springer, New York (1975)

    Book  MATH  Google Scholar 

  12. Feng, Z., Velasco-Hernndez, J.X.: Competitive exclusion in a vector-host model for the dengue fever. J. Math. Biol. 35(5), 523–544 (1997)

    Article  MATH  Google Scholar 

  13. Göllmann, L., Kern, D., Maurer, H.: Optimal control problems with delays in state and control variables subject to mixed control-state constraints. Optim. Contr. Appl. Met. 30(4), 341–365 (2010)

    Article  Google Scholar 

  14. Guo, S., Li, X., Ghosh, M.: Analysis of a dengue disease model with nonlinear incidence. Discrete Dyn. Nat. Soc. Article ID 320581, 10 pages (2013). https://doi.org/10.1155/2013/320581

  15. Gakkhar, S., Mishra, A.: A dengue model incorporating saturation incidence and human migration. AIP Conf. Proc. 1651, 64–69 (2015)

    Article  Google Scholar 

  16. Hethcote, H.W., van den Driessche, P.: Some epidemiological models with nonlinear incidence. J. Math. Biol. 29(3), 271–287 (1991)

    Article  MATH  Google Scholar 

  17. Hale, J., Lunel, S.M.V.: Introduction to Functional Differential Equations. Springer, New York (1993)

    Book  MATH  Google Scholar 

  18. Kuang, Y.: Delay Differential Equations: With Applications in Population Dynamics. Academic Press (1993)

  19. Laarabi, H., Abta, A., Hattaf, K.: Optimal control of a delayed SIRS epidemic model with vaccination and treatment. Acta Biotheor. 63(2), 87–97 (2015)

    Article  Google Scholar 

  20. Liu, W., Levin, S., Iwasa, Y.: Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 23(2), 187–204 (1986)

    Article  MATH  Google Scholar 

  21. Li, M., Sun, G., Yakob, L., et al.: The driving force for 2014 dengue outbreak in Guangdong. China. PLoS One. 11(11), 1–19 (2016)

    Google Scholar 

  22. Martcheva, M.: An Introduction to Mathematical Epidemiology. Spinger, New York (2015)

    Book  MATH  Google Scholar 

  23. Marino, S., Hogue, I.B., Ray, C., et al.: A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theoret. Biol. 254(1), 178–196 (2009)

    Article  MATH  Google Scholar 

  24. Magal, P., Mccluskey, C.C., Webb, G.F.: Lyapunov functional and global asymptotic stability for an infection-age model. Appl. Anal. 9(7), 1109–1140 (2010)

    Article  MATH  Google Scholar 

  25. Tewa, J., Dimi, J., Bowong, S.: Lyapunov functions for a dengue disease transmission model. Chaos Solitons & Fractal. 39(2), 936–941 (2009)

    Article  MATH  Google Scholar 

  26. World Health Organization (WHO), web page: https://www.who.int/zh/

  27. World Health Organization (2020). Available from: https://www.who.int/en/news-room/fact-sheets/detail/dengue-and-severe-dengue

  28. Wu, J., Lun, Z., James, A.A., et al.: Dengue fever in mainland China. Am. J. Trop. Med. Hyg. 83(3), 664–671 (2010)

    Article  Google Scholar 

  29. Wang, W., Zhao, X.Q.: A nonlocal and time-delayed reaction-diffusion model of dengue transmission. Siam J. Appl. Math. 71(1), 147–168 (2011)

    Article  MATH  Google Scholar 

  30. Wang, Z., Zhao, X.Q.: Global dynamics of a time-delayed dengue transmission model. Can. Appl. Math. Q. 20(1), 89–113 (2012)

    MATH  Google Scholar 

  31. Xu, R., Du, Y.: A delayed SIR epidemic model with saturation incidence and a constant infectious period. J. Appl. Math. Comput. 35(1–2), 229–250 (2011)

    Article  MATH  Google Scholar 

  32. Yang, H., Wei, H., Li, X.: Global stability of an epidemic model for vector-borne disease. J. Syst. Sci. Complex. 23, 279–292 (2010)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 11871316, 11801340) and the Natural Science Foundation of Shanxi Province, China (Nos. 201801D121006, 201801D221007).

Author information

Author notes

  1. X. Tian, R. Xu and C. Song: These authors contributed equally to this work.

Authors and Affiliations

  1. Complex Systems Research Center, Shanxi University, Taiyuan, 030006, People’s Republic of China

    Bian Wang, Xiaohong Tian, Rui Xu & Chenwei Song

Authors
  1. Bian Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaohong Tian
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rui Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Chenwei Song
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Rui Xu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, B., Tian, X., Xu, R. et al. Threshold dynamics and optimal control of a dengue epidemic model with time delay and saturated incidence. J. Appl. Math. Comput. 69, 871–893 (2023). https://doi.org/10.1007/s12190-022-01766-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01766-3

Keywords