Skip to main content

Advertisement

Springer Nature Link
Log in

A mathematical model for human papillomavirus and its impact on cervical cancer in India

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

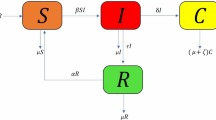
Abstract

Cervical cancer is one of the most common cancers among women globally, with more than three quarters of its global burden occurring in developing countries and one of the most common cancer among Indian women. Cervical cancer cases (more than 95%) are linked to infection with high-risk human papillomaviruses (HPV). HPV is mostly transmitted through sexual contact, and majority become infected with HPV shortly after sexual activity begins. This paper develops a mathematical model for HPV transmission and its impact on cervical cancer. The basic properties of the system are discussed in detail. Using the next-generation matrix method, we obtain the basic reproduction number and prove that the disease-free and endemic equilibrium are globally asymptotically stable under certain conditions. Numerical solutions of the proposed model are carried out using the fourth-order Runge–Kutta method to demonstrate our theoretical results.The developed model is applied to reported data of women HPV transmission from 2016 to 2020 obtained from the HPV Information center and Indian Council of Medical Research. From the data, we estimate parameter values and identify the key parameters that influence transmission via sensitivity analysis for this model. The simulation results match the HPV epidemic data in India approximately.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. World Health Organization. Global strategy to accelerate the elimination of cervical cancer as a public health problem (2020). https://www.who.int/publications/i/item/9789240014107 Accessed 05 March 2021

  2. Ferlay, J., Ervik, M., Lam, F., Colombet, M., Mery, L., Piñeros, M., Znaor, A., Soerjomataram, I., Bray, F.: Global Cancer Observatory: Cancer Today. Lyon, France: International Agency for Research on Cancer (2020). https://gco.iarc.fr/today Accessed 05 March 2021

  3. Bruni, L., Albero, G., Serrano, B., Mena, M., Gomez, D., Muno, J., Bosch, F., de Sanjose, S.: ICO/IARC Information Centre on HPV and Cancer (HPV Information Centre). Human Papillomavirus and Related Diseases in India. Summary Report 10 December 2018. https://hpvcentre.net/ Accessed 05 March 2021

  4. Sung, H., Ferlay, J., Siegel, R., Laversanne, M., Soerjomataram, I., Jemal, A., Bray, F.: Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 71(3), 209–249 (2021). https://doi.org/10.3322/caac.21660

    Article  Google Scholar 

  5. Indian Council of Medical Research: Consensus document for management of cancer cervix. https://main.icmr.nic.in/sites/default/files/reports/Cervix

  6. Franceschi, S., Rajkumar, R., Snijders, P., Arslan, A., Mahe, C., Plummer, M., Sankaranarayanan, R., Cherian, J., Meijer, C., Weiderpass, E.: Papillomavirus infection in rural women in southern India. Br. J. Cancer 92(3), 601–606 (2005). https://doi.org/10.1038/sj.bjc.6602348

    Article  Google Scholar 

  7. Huo, H.F., Chen, R., Wang, X.Y.: Modelling and stability of HIV/AIDS epidemic model with treatment. Appl. Math. Model. 40(13–14), 6550–6559 (2016). https://doi.org/10.1016/j.apm.2016.01.054

    Article  MATH  Google Scholar 

  8. Sarkar, K., Khajanchi, S., Nieto, J.J.: Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 139, 110049–16 (2020). https://doi.org/10.1016/j.chaos.2020.110049

    Article  Google Scholar 

  9. Tyagi, S., Martha, S.C., Abbas, S., Debbouche, A.: Mathematical modeling and analysis for controlling the spread of infectious diseases. Chaos Solitons Fractals 144, 110707 (2021). https://doi.org/10.1016/j.chaos.2021.110707

    Article  MATH  Google Scholar 

  10. Srivastav, A.K., Ghosh, M.: Modeling the transmission dynamics of malaria with saturated treatment: a case study of India. J. Appl. Math. Comput. 67(1–2), 519–540 (2021). https://doi.org/10.1007/s12190-020-01469-7

    Article  MATH  Google Scholar 

  11. Su, R., Yang, W.: Global stability of a diffusive HCV infections epidemic model with nonlinear incidence. J. Appl. Math. Comput. (2021). https://doi.org/10.1007/s12190-021-01637-3

    Article  MATH  Google Scholar 

  12. Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 115, 700–721 (1927). https://doi.org/10.1098/rspa.1927.0118

    Article  MATH  Google Scholar 

  13. Ross, R.: The Prevention of Malaria, 2nd edn. John Murray, London (1911)

    Google Scholar 

  14. Lee, S.L., Tameru, A.M.: A mathematical model of Human Papillomavirus (HPV) in the United States and its impact on cervical cancer. J. Cancer 3, 262–268 (2012). https://doi.org/10.7150/jca.4161

    Article  Google Scholar 

  15. Obeng Denteh, W., Afrifa, R., Barnes, B., Addo, K.: Modeling the epidemiology of Human Papilloma Virus infection and Vaccination and its impact on Cervical Cancer in Ghana. J. Sci. Res. Rep. 3(19), 2501–2518 (2014). https://doi.org/10.9734/JSRR/2014/11019

    Article  Google Scholar 

  16. Berhe, H.W., Alarydah, M.: Computational modeling of human papillomavirus with impulsive vaccination. Nonlinear Dyn. 103, 925–946 (2021). https://doi.org/10.1007/s11071-020-06123-2

    Article  Google Scholar 

  17. Saldaña, F., Korobeinikov, A., Barradas, I.: Optimal control against the human papillomavirus: protection versus eradication of the infection. Abstr. Appl. Anal. (2019). https://doi.org/10.1155/2019/4567825

    Article  MATH  Google Scholar 

  18. Olson, B., Gribble, B., Dias, J., Curryer, C., Vo, K., Kowal, P., Byles, J.: Cervical cancer screening programs and guidelines in low- and middle-income countries. Int. J. Gynaecol. Obstet. 134(3), 239–246 (2016). https://doi.org/10.1016/j.ijgo.2016.03.011

    Article  Google Scholar 

  19. Johnson, H.C., Lafferty, E.I., Eggo, R.M., Louie, K., Soldan, K., Waller, J., Edmunds, W.J.: Effect of HPV vaccination and cervical cancer screening in England by ethnicity: a modelling study. Lancet Public Health 3(1), 44–51 (2018). https://doi.org/10.1016/S2468-2667(17)30238-4

    Article  Google Scholar 

  20. Domingo, E.J., Noviani, R., Noor, M.R.M., Ngelangel, C.A., Limpaphayom, K.K., Van Thuan, T., Louie, K.S., Quinn, M.A.: Epidemiology and prevention of cervical cancer in Indonesia, Malaysia, the Philippines, Thailand and Vietnam. Vaccine 26, 71–79 (2008). https://doi.org/10.1016/j.vaccine.2008.05.039

    Article  Google Scholar 

  21. Choi, Y.H., Jit, M., Gay, N., Cox, A., Garnett, G.P., Edmunds, W.J.: Transmission dynamic modelling of the impact of human papillomavirus vaccination in the united kingdom. Vaccine 28(24), 4091–4102 (2010). https://doi.org/10.1016/j.vaccine.2009.09.125

    Article  Google Scholar 

  22. Fatoorehchi, H., Abolghasemi, H., Zarghami, R., Rach, R.: Feedback control strategies for a cerium-catalyzed Belousov–Zhabotinsky chemical reaction system. Can. J. Chem. Eng. 93(7), 1212–1221 (2015). https://doi.org/10.1002/cjce.22213

    Article  MATH  Google Scholar 

  23. Fatoorehchi, H., Ehrhardt, M.: Numerical and semi-numerical solutions of a modified Thévenin model for calculating terminal voltage of battery cells. J. Energy Stor. 45, 103746 (2022). https://doi.org/10.1016/j.est.2021.103746

    Article  Google Scholar 

  24. Egbelowo, O., Harley, C., Jacobs, B.: Nonstandard finite difference method applied to a linear pharmacokinetics model. Bioengineering (2017). https://doi.org/10.3390/bioengineering4020040

    Article  Google Scholar 

  25. Egbelowo, O.F.: Nonstandard finite difference approach for solving 3-compartment pharmacokinetic models. Int. J. Numer. Methods Biomed. Eng. 34(9), 3114 (2018). https://doi.org/10.1002/cnm.3114

    Article  Google Scholar 

  26. Egbelowo, O.: Nonlinear elimination of drugs in one-compartment pharmacokinetic models: nonstandard finite difference approach for various routes of administration. Math. Comput. Appl. 23(2), 27 (2018). https://doi.org/10.3390/mca23020027

    Article  Google Scholar 

  27. Yang, X., Chen, L., Chen, J.: Permanence and positive periodic solution for the single-species nonautonomous delay diffusive models. Comput. Math. Appl. 32(4), 109–116 (1996). https://doi.org/10.1016/0898-1221(96)00129-0

    Article  MATH  Google Scholar 

  28. Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.J.: On the definition and the computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28(4), 365–382 (1990). https://doi.org/10.1007/BF00178324

    Article  MATH  Google Scholar 

  29. Jia, J., Xiao, J.: Stability analysis of a disease resistance SEIRS model with nonlinear incidence rate. Adv. Differ. Equ. (2018). https://doi.org/10.1186/s13662-018-1494-1

    Article  MATH  Google Scholar 

  30. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002). https://doi.org/10.1016/S0025-5564(02)00108-6

    Article  MATH  Google Scholar 

  31. Cheng, Y., Wang, J., Yang, X.: On the global stability of a generalized cholera epidemiological model. J. Biol. Dyn. 6(2), 1088–1104 (2012). https://doi.org/10.1080/17513758.2012.728635

    Article  MATH  Google Scholar 

  32. LaSalle, J.P.: The Stability of Dynamical Systems. Society for Industrial and Applied Mathematics, Philadelphia (1976)

    Book  MATH  Google Scholar 

  33. Vargas De Leon, C.: Construction of classic Lyapunov functions for classic SIS, SIR and SIRS epidemic model with variable population size. Revista Electronica 26, 1–12 (2009)

    Google Scholar 

  34. Meskaf, A., Khyar, O., Danane, J., Allali, K.: Global stability analysis of a two-strain epidemic model with non-monotone incidence rates. Chaos Solitons Fractals 133, 109647–8 (2020). https://doi.org/10.1016/j.chaos.2020.109647

    Article  MATH  Google Scholar 

  35. McCluskey, C.C.: Global stability for a class of mass action systems allowing for latency in tuberculosis. J. Math. Anal. Appl. 338(1), 518–535 (2008). https://doi.org/10.1016/j.jmaa.2007.05.012

    Article  MATH  Google Scholar 

  36. United Nations, Department of Economic and Social Affairs, Population Division. World Population Prospects 2019, Online Edition. Rev. 1. https://population.un.org/wpp/Download/Standard/Population/ Accessed 02 January 2021

  37. Gupta, N., Chauhan, A.S., Prinja, S., Pandey, A.K.: Impact of COVID-19 on outcomes for patients with cervical cancer in India. JCO Glob. Oncol. 7, 716–725 (2021). https://doi.org/10.1200/GO.20.00654

    Article  Google Scholar 

Download references

Acknowledgements

The research work of the First author Mr. R. Praveen Kumar is suppoted by INSPIRE Fellowship (IF180053), Department of Science and Technology, Govt of India.

Author information

Author notes

  1. M. Kuppusamy, O. F. Egbelowo: These authors contributed equally to this work.

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Tiruchirappalli, TamilNadu, 620015, India

    Praveen Kumar Rajan & Murugesan Kuppusamy

  2. Department of Integrative Biology, The University of Texas at Austin, Austin, TX, 78712, USA

    Oluwaseun F. Egbelowo

Authors
  1. Praveen Kumar Rajan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Murugesan Kuppusamy
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Oluwaseun F. Egbelowo
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

PKR: Conceptualization, Methodology, Software, Formal analysis, Writing- Original draft preparation. MK: Supervision, Writing-Original draft preparation,Methodology, Writing-Reviewing and Editing. OE: Formal analysis and Methodology.

Corresponding author

Correspondence to Murugesan Kuppusamy.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rajan, P.K., Kuppusamy, M. & Egbelowo, O.F. A mathematical model for human papillomavirus and its impact on cervical cancer in India. J. Appl. Math. Comput. 69, 753–770 (2023). https://doi.org/10.1007/s12190-022-01767-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01767-2

Keywords

Mathematics Subject Classification