Skip to main content

Advertisement

Springer Nature Link
Log in

On analysis of fractional order HIV infection model with the adaptive immune response under Caputo operator

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

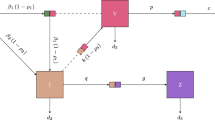
The present work investigates the fractional dynamics of a system concerned with the human immuno-deficiency virus (HIV) disease with cytotoxic T-lymphocyte (CTL), anti-bodies and two saturated rates. The system is characterized by five non-linear compartments which examine the conditions of un-infected cells, infected cells, cells without HIV, CTL immune responses, and antibodies. This problem aims to examine the existence and uniqueness of some well-known theory of fixed point. More precisely, Ulam Hyer’s stability was used to analyze the system’s stability. The approximate solution is carried out using fractional Adams Bash-forth method techniques. Using MATLAB, some numerical simulations are carried out by the obtained scheme at different non-integer order along with the comparison of integer order.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Silva, C.J., Torres, D.F.M.: A TB/AIDS coinfection model and optimal control treatment. Discrete Contin. Dyn. Syst. 35(9), 4639–4663 (2015)

    MathSciNet  MATH  Google Scholar 

  2. Nowak, M.A., May, R.M.: Mathematical biology of HIV infection: an tigenic variation and diversity threshold. Math. Biosci. 106(1), 1–21 (1991)

    MATH  Google Scholar 

  3. Perelson, A.S., Nelson, P.W.: Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 41(1), 3–44 (1999)

    MathSciNet  MATH  Google Scholar 

  4. Tabit, Y., Meskaf, A., Allali, K.: Mathematical analysis of HIV model with two saturated rates, CTL and antibody responses. World J. Model. Simul. 12(2), 137–146 (2016)

    Google Scholar 

  5. Zhou, X., Song, X., Shi, X.: A differential equation model of HIV infection of \(CD4^+ T\)-cells with cure rate. J. Math. Anal. Appl. 342(2), 1342–1355 (2008)

    MathSciNet  MATH  Google Scholar 

  6. Liu, X., Wang, H., Ma, W.: Global stability of an HIV pathogenesis model with cure rate. Nonlinear Anal. RWA 12(6), 2947–2961 (2011)

    MathSciNet  MATH  Google Scholar 

  7. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Method of There Solution and Some of There Applications. Elsevier (1998)

  8. Granas, A., Dugundji, J.: Fixed Point Theory. Springer, New York (2003)

    MATH  Google Scholar 

  9. Atangana, A., Owlabi, K.M.: New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 13, 3 (2018)

    MathSciNet  Google Scholar 

  10. Ali, R., Pan, K., Ali, A.: Two generalized successive overrelaxation methods for solving absolute value equations. Math. Theory Appl. 40(4), 44–55 (2020)

    Google Scholar 

  11. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)

    MATH  Google Scholar 

  12. Hilfer, R.: Threefold Introduction to Fractional Derivatives. Wiley, Germany (2008)

    Google Scholar 

  13. Kilbas, A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  14. Ali, R., Khan, I., Ali, A., Mohamed, A.: Two new generalized iteration methods for solving absolute value equations using M-matrix. AIMS Math. 7(5), 8176–8187 (2022)

    MathSciNet  Google Scholar 

  15. Podlubny, I.: Fractional Differential Equations, Mathematics in Science and Engineering. Academic Press, New York (1999)

  16. Lakshmikantham, V., Leela, S., Vasundhara, J.: Theory of Fractional Dynamic Systems. Cambridge Academic Publishers, Cambridge (2009)

    MATH  Google Scholar 

  17. Ali, R., Pan, K.: The new iteration methods for solving absolute value equations. Appl. Math. 66, 1–14 (2021)

    MathSciNet  Google Scholar 

  18. Singh, H.: Analysis of drug treatment of the fractional HIV infection model of \(CD4_+T\)-cells. Chaos Solitons Fract. 146, 110868 (2020)

    Google Scholar 

  19. Anwarud, D., Li, Y.: Theoretical and numerical analysis of hepatitis B virus model with non-singular kernels. Waves Random Complex Media 66, 1–20 (2022)

    Google Scholar 

  20. ur Rahman, M., Arfan, M., Shah, Z., Alzahrani, E.: Evolution of fractional mathematical model for drinking under Atangana–Baleanu Caputo derivatives. Phys. Scr. 96, 115203 (2021)

    Google Scholar 

  21. Singh, H.: Jacobi collocation method for the fractional advection-dispersion equation arising in porous media. Numer. Methods Partial Differ. Equ. (2020). https://doi.org/10.1002/num.22674

    Article  Google Scholar 

  22. Singh, H.: Numerical simulation for fractional delay differential equations. Int. J. Dyn. Control 6, 66 (2020)

    Google Scholar 

  23. Singh, H., Singh, A.K.: Numerical simulation for fractional Bloch equation arising in nuclear magnetic resonance. Nonlinear Stud. 28, 531–548 (2021)

    MathSciNet  Google Scholar 

  24. Ali, Zeeshan, Rabiei, Faranak, Rashidi, Mohammad M., Khodadadi, Touraj: A fractional-order mathematical model for COVID-19 outbreak with the effect of symptomatic and asymptomatic transmissions. Eur. Phys. J. Plus 137(3), 1–20 (2022)

    Google Scholar 

  25. Ali, R., Pan, K.: The solution of the absolute value equations using two generalized accelerated overrelaxation methods. Asian Eur. J. Math. 15(8), 2250154 (2022)

    MathSciNet  MATH  Google Scholar 

  26. Ali, Zeeshan, Rabiei, Faranak, Shah, Kamal, Khodadadi, Touraj: Fractal–fractional order dynamical behavior of an HIV/AIDS epidemic mathematical model. Eur. Phys. J. Plus 136(1), 1–17 (2021)

    Google Scholar 

  27. Ali, R., Ali, A., Iqbal, S.: Iterative methods for solving absolute value equations. J. Math. Comput. Sci. 26(4), 322–329 (2022)

    Google Scholar 

  28. Ali, Zeeshan, Faranak, Rabiei, Kamal, Shah, Majid, Zanariah Abdul: Dynamics of SIR mathematical model for COVID-19 outbreak in Pakistan under fractal–fractional derivative. Fractals 29(05), 2150120 (2021)

    MATH  Google Scholar 

  29. Hajiseyedazizi, Sayyedeh Narges, Samei, Mohammad Esmael, Alzabut, Jehad: On multi-step methods for singular fractional q-integro-differential equations. Open Math. 19(1), 1378–1405 (2021)

    MathSciNet  MATH  Google Scholar 

  30. Ali, Zeeshan, Rabiei, Faranak, Shah, Kamal, Khodadadi, Touraj: Modeling and analysis of novel COVID-19 under fractal–fractional derivative with case study of Malaysia. Fractals 29(01), 2150020 (2021)

    MATH  Google Scholar 

  31. Ali, R., Pan, K.: Two new fixed point iterative schemes for absolute value equations. Jpn. J. Ind. Appl. Math. (2022). https://doi.org/10.1007/s13160-022-00526-x

    Article  MATH  Google Scholar 

  32. Ali, Zeeshan, Rabiei, Faranak, Shah, Kamal, Khodadadi, Touraj: Qualitative analysis of fractal–fractional order COVID-19 mathematical model with case study of Wuhan. Alex. Eng. J. 60(1), 477–489 (2021)

    Google Scholar 

  33. Zha, T.-H., Castillo, O., Jahanshahi, H., Yusuf, A., Alassafi, M.O., Alsaadi, F.E., Chu, Y.-M.: A fuzzy-based strategy to suppress the novel coronavirus (2019-NCOV) massive outbreak. Appl. Comput. Math. 66, 160–176 (2021)

    MathSciNet  MATH  Google Scholar 

  34. Cheng, Y., Zhang, H., Zhang, W., et al.: Novel algebraic criteria on global Mittag–Leffler synchronization for FOINNs with the Caputo derivative and delay. J. Appl. Math. Comput. (2021). https://doi.org/10.1007/s12190-021-01672-0

    Article  MATH  Google Scholar 

  35. Zhang, H., Cheng, Y., Zhang, H., Zhang, W., Cao, J.: Hybrid control design for Mittag–Leffler projective synchronization on FOQVNNs with multiple mixed delays and impulsive effects. Math. Comput. Simul. 197, 341–357 (2022). https://doi.org/10.1016/j.matcom.2022.02.022

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhang, H., Cheng, J., Zhang, H., Zhang, W., Cao, J.: Quasi-uniform synchronization of Caputo type fractional neural networks with leakage and discrete delays. Chaos Solitons Fract. 152, 111432 (2021). https://doi.org/10.1016/j.chaos.2021.111432

    Article  MathSciNet  MATH  Google Scholar 

  37. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    MATH  Google Scholar 

  38. Algehyne, E.A., Ibrahim, M.: Fractal–fractional order mathematical vaccine model Of COVID-19 under non-singular kernel. Chaos Solitons Fract. 66, 111150 (2021)

    MathSciNet  Google Scholar 

  39. Shah, Kamal, Seadawy, Aly, Alrabaiah, Hussam, Baleanu, Dumitru: On a new conceptual mathematical model dealing the current novel coronavirus-19 infectious disease. Results Phys. 19, 103510 (2020)

    Google Scholar 

  40. Huynh, L.N., Luc, N.H., Baleanu, D.: Recovering the space source term for the fractional–diffusion equation with Caputo–Fabrizio derivative. J. Inequal. Appl. 2021(1), 1–20 (2021)

    MathSciNet  MATH  Google Scholar 

  41. Baleanu, D., Jajarmi, A., Mohammadi, H., Rezapour, S.: A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fract. 134, 109705 (2020)

    MathSciNet  MATH  Google Scholar 

  42. Qureshi, S., Rangaig, N.A., Baleanu, D.: New numerical aspects of Caputo–Fabrizio fractional derivative operator. Mathematics 7(4), 374 (2019)

    Google Scholar 

  43. Kumar, D., Singh, J., Baleanu, D.: A new analysis of the Fornberg–Whitham equation pertaining to a fractional derivative with Mittag–Leffler-type kernel. Eur. Phys. J. Plus 133(2), 1–10 (2018)

    Google Scholar 

  44. Din, Anwarud, Li, Yongjin, Khan, Tahir, Zaman, Gul: Mathematical analysis of spread and control of the novel corona virus (COVID-19) in China. Chaos Solitons Fract. 141, 110286 (2020)

    MathSciNet  MATH  Google Scholar 

  45. Solís-Pérez, J.E., Gómez-Aguilar, J.F., Atangana, A.: Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag–Leffler laws. Chaos Solitons Fract. 114, 175–185 (2018)

    MathSciNet  MATH  Google Scholar 

  46. Din, A., Li, Y., Khan, N.M., Khan, Z.U., Liu, P.: On analysis of fractional order mathematical model of hepatitis B using Atangana-Baleanu Caputo (ABC) derivative. Fractals 66, 2240017 (2021)

    MATH  Google Scholar 

  47. Atangana, A., Goufo, E.F.D.: Some misinterpretations and lack of understanding in differential operators with no singular kernels. Open Phys. 18(1), 594–612 (2020)

    Google Scholar 

  48. Atangana, A.: Fractal–fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fract. 102, 396–406 (2017)

    MathSciNet  MATH  Google Scholar 

  49. Zeeshan, A.L.İ, Akbar, Z.A.D.A., Kamal, S.H.A.H.: Ulam stability results for the solutions of nonlinear implicit fractional order differential equations. Hacettepe J. Math. Stat. 48(4), 1092–1109 (2018)

    MathSciNet  MATH  Google Scholar 

  50. Ali, Z., Zada, A., Shah, K.: On Ulam’s stability for a coupled systems of nonlinear implicit fractional differential equations. Bull. Malays. Math. Sci. Soc. 42(5), 2681–2699 (2019)

    MathSciNet  MATH  Google Scholar 

  51. Qureshi, S., Atangana, A.: Fractal–fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data. Chaos Solitons Fract. 136, 109812 (2020)

    MathSciNet  Google Scholar 

  52. Atangana, A.: Modelling the spread of COVID-19 with new fractal–fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fract. 136, 109860 (2020)

    MathSciNet  Google Scholar 

  53. Arfan, M., Alrabaiah, H., Ur Rahman, M., Sun, Y.L., Hashim, A.S., Pansera, B.A., Ahmadian, A., Salahshour, S.: Investigation of fractal–fractional order model of COVID-19 in Pakistan under Atangana–Baleanu Caputo (ABC) derivative. Results Phys. 24, 104046 (2021)

    Google Scholar 

  54. Din, A., Li, Y., Yusuf, A., Ali, A.I.: Caputo type fractional operator applied to hepatitis B system. Fractals 66, 2240023 (2021)

    MATH  Google Scholar 

  55. Khan, F.M., Ali, A., Khan, Z.U., Alharthi, M.R., Abdel-Aty, A.-H.: Qualitative and quantitative study of Zika virus epidemic model under Caputo’s fractional differential operator. Phys. Scr. 96(12), 124030 (2021)

    Google Scholar 

  56. Gómez, J.F., et al.: Fractional Derivatives with Mittag–Leffler Kernel. Springer (2019)

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Central South University, Changsha, 410083, Hunan, People’s Republic of China

    Ashfaq Ahmad, Ijaz Ahmad & Rashid Ali

  2. Department of Basic Sciences and Humanities, CECOS University of IT and Emerging Sciences, Peshawar, Pakistan

    Muhammad Ibrahim

Authors
  1. Ashfaq Ahmad
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ijaz Ahmad
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Rashid Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Muhammad Ibrahim
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ashfaq Ahmad.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmad, A., Ahmad, I., Ali, R. et al. On analysis of fractional order HIV infection model with the adaptive immune response under Caputo operator. J. Appl. Math. Comput. 69, 1845–1863 (2023). https://doi.org/10.1007/s12190-022-01804-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01804-0

Keywords

Mathematics Subject Classification