Skip to main content

Advertisement

Springer Nature Link
Log in

Dynamic analysis and bifurcation control of a fractional-order cassava mosaic disease model

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

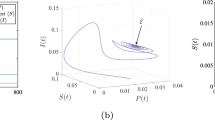
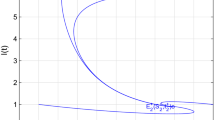
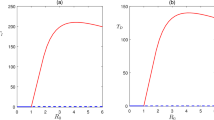
In this paper, a fractional-order model including healthy cassava, infected cassava, and infected vectors is proposed to study the transmission dynamics of cassava mosaic disease. Firstly, the non-negativity and boundedness of the solutions in the system and the stability of all feasible equilibrium points of the system are strictly discussed. Hopf bifurcation induced by the disease transmission rate from the vectors to the healthy cassava is studied for the proposed system. Secondly, a novel periodic pulse feedback controller is proposed to suppress the bifurcation phenomenon. The expression of the bifurcation point of the controlled system is given with the help of the linearized average system. It is shown that the stability performance is extremely excellent with the help of the proposed controller and that the control effect is independent of pulse width. Numerical simulations are performed to validate the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Legg, J., Somado, E.A., Barker, I., Beach, L., Ceballos, H., et al.: A global alliance declaring war on cassava viruses in Africa. Food Secur. 6(2), 231–248 (2014)

    Article  Google Scholar 

  2. Sinha, S., Samad, A.: First Report of Cucumber mosaic virus Associated with Yellowing Mosaic Disease of African Basil (Ocimum gratissimum) in India. Plant Dis. 103(1), 167–167 (2019)

    Article  Google Scholar 

  3. Gao, S.Q., Qu, J., Chua, N.H., Ye, J.: A new strain of Indian cassava mosaic virus causes a mosaic disease in the biodiesel crop Jatropha curcas. Arch. Virol. 155(4), 607–612 (2010)

    Article  Google Scholar 

  4. Otim-Nape, G.W., Thresh, J.M.: The Current Pandemic of Cassava Mosaic Virus Disease in Uganda. Springer, Cham (1998)

    Book  Google Scholar 

  5. Thresh, J. M., Otim-Nape, G. W., Legg, J. P., Fargette, D.: African cassava mosaic virus disease: the magnitude of the problem. Afr. J. Root Tuber Crops. (1997)

  6. Wang, H.L., Cui, X.Y., Wang, X.W., Liu, S.S., Zhang, X.: First report of Sri Lankan cassava mosaic virus infecting cassava in Cambodia. Plant Dis. 100(5), 1029–1029 (2016)

    Article  Google Scholar 

  7. Wang, D., Yao, X., Huang, G., Shi, T., Wang, G., Ye, J.: First report of Sri Lankan cassava mosaic virus infected cassava in China. Plant Dis. 103(6), 1437–1438 (2019)

    Article  Google Scholar 

  8. Verdaguer, B., de Kochko, A., Fux, C.I., Beachy, R.N., Fauquet, C.: Functional organization of the cassava vein mosaic virus (csvmv) promoter. Plant Mol. Biol. 37(6), 1055–1067 (1998)

    Article  Google Scholar 

  9. Basir, F.A., Kyrychko, Y.N., Blyuss, K.B., Ray, S.: Effects of vector maturation time on the dynamics of cassava mosaic disease. Bull. Math. Biol. 83(8), 87 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  10. Jittamai, P., Chanlawong, N., Atisattapong, W., Anlamlert, W., Buensanteai, N.: Reproduction number and sensitivity analysis of cassava mosaic disease spread for policy design. Math. Biosci. Eng. 18(5), 5069–5093 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  11. Basir, F.A., Roy, P.K.: Dynamics of mosaic disease with roguing and delay in Jatropha curcas plantations. J. Appl. Math. Comput. 58(1–2), 1–31 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  12. Basir, F.A., Ray, S.: Impact of farming awareness based roguing, insecticide spraying and optimal control on the dynamics of mosaic disease. Ric. Mat. 69(2), 393–412 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. Maity, S., Mandal, P.S.: A comparison of deterministic and stochastic plant-vector-virus models based on probability of disease extinction and outbreak. Bull. Math. Biol. 84(3), 41 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  14. Rakshit, N., Basir, F.A., Banerjee, A., Ray, S.: Dynamics of plant mosaic disease propagation and the usefulness of roguing as an alternative biological control. Ecol. Complex. 38, 15–23 (2019)

    Article  Google Scholar 

  15. Fahad, A.B., Blyuss, K.B., Santanu, R.: Modelling the effects of awareness-based interventions to control the mosaic disease of Jatropha curcas. Ecol. Complex. 36, 92–100 (2019)

    Google Scholar 

  16. Xu, F., Cressman, R., Shu, X.B., Liu, X.Z.: A series of new chaotic attractors via switched linear integer order and fractional order differential equations. Int. J. Bifurcation Chaos. 25(1), 1550008 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  17. Benmalek, M., Charef, A.: Digital fractional order operators for R-wave detection in electrocardiogram signal. IET Signal Process. 3(5), 381–391 (2009)

    Article  Google Scholar 

  18. Bagley, R.L., Calico, R.A.: Fractional order state equations for the control of viscoelasticallydamped structures. J. Guid. Control. Dyn. 1(4), 431–436 (1991)

    Google Scholar 

  19. Magin, R.L.: Fractional calculus in bioengineering, part 1. Crit. Rev. Biomed. Eng. 32(1), 1–104 (2004)

    Article  Google Scholar 

  20. Magin, R.L.: Fractional calculus in bioengineering, part 2. Crit. Rev. Biomed. Eng. 32(2), 105–193 (2004)

    Article  Google Scholar 

  21. Magin, R.L.: Fractional calculus in bioengineering, part 3. Crit. Rev. Biomed. Eng. 32(3–4), 195–377 (2004)

    Article  Google Scholar 

  22. Yuriy, A., Rossikhin, Marina, V.: Shitikova, Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 50(1), 15–67 (1997)

  23. Mainardi, F.: Fractional calculus: some basic problems in continuum and statistical mechanics. COURSES AND LECTURES- INTERNATIONAL CENTRE FOR MECHANICAL SCIENCES (1997)

  24. Xu, F., Lai, Y.Z., Shu, X.B.: Chaos in integer order and fractional order financial systems and their synchronization. Chaos Solitons Fractals 117, 125–136 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  25. Baillie, R.T.: Long memory processes and fractional integration in econometrics. J. Econom. 73(1), 5–59 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  26. Zheng, K., Zhou, X.L., Wu, Z.H. et al.: Hopf bifurcation controlling for a fractional order delayed paddy ecosystem in the fallow season. Adv. Differ. Equ. (307) (2019)

  27. Baishya, C., Achar, S.J., Veeresha, P., Prakasha, D.G.: Dynamics of a fractional epidemiological model with disease infection in both the populations. Chaos 31(4), 043130 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  28. Moustafa, M., Mohd, M.H., Ismail, A.I., Abdullah, F.A.: Dynamical analysis of a fractional order eco-epidemiological model with nonlinear incidence rate and prey refuge. J. Appl. Math. Comput. 65(1–2), 623–650 (2020)

    MathSciNet  MATH  Google Scholar 

  29. Acay, B., Inc, M., Khan, A., Yusuf, A.: Fractional methicillin-resistant Staphylococcus aureus infection model under caputo operator. J. Appl. Math. Comput. 67(1), 755–783 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  30. Majee, S., Adak, S., Jana, S., Mandal, M., Kar, T.K.: Complex dynamics of a fractional-order sir system in the context of covid-19. J. Appl. Math. Comput. 67(1), 755–783 (2021)

    MathSciNet  MATH  Google Scholar 

  31. Akrami, M.H., Atabaigi, A.: Hopf and forward bifurcation of an integer and fractional-order sir epidemic model with logistic growth of the susceptible individuals. J. Appl. Math. Comput. 64(1–2), 615–633 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  32. Mondal, S., Biswas, M., Bairagi, N.: Local and global dynamics of a fractional-order predator-prey system with habitat complexity and the corresponding discretized fractional-order system. J. Appl. Math. Comput. 63(1–2), 311–340 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  33. Henryk, C., Aliza, H.S., Iris, S., Rena, G., Murad, G.: The incredible journey of begomoviruses in their whitefly vector. Viruses 9(10), 273 (2017)

    Article  Google Scholar 

  34. Alidousti, J.: Stability and bifurcation analysis for a fractional prey–predator scavenger model. Appl. Math. Model. 81, 342–355 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  35. Das, M., Samanta, G.P.: A delayed fractional order food chain model with fear effect and prey refuge. Math. Comput. Simul. 178, 218–245 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  36. Db, A., Jr, A., Hab, C. et al.: Impact of predator incited fear and prey refuge in a fractional order prey predator model. Chaos Solitons Fractals 142(110420) (2020)

  37. Hale, J., Lunel, S.V.: An Introduction to Functional Differential Equations (1993)

  38. Haubold, H.J., Mathai, A.M., Saxena, R.K.: Mittag–Leffler functions and their applications. J. Appl. Math. (298628) (2009)

  39. Salman, S.M.: Memory and media coverage effect on an HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 385, 113203 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  40. Jiang, Z., Zhao, Y., Bai, X., Zhang, Z.: Bifurcation and control of a planktonic ecological system with double delays by delayed feedback control. J. Frankl. Inst. Eng. Appl. Math. 358(7), 3609–3632 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhou, W.G., Huang, C.D., Xiao, M., Cao, J.D.: Hybrid tactics for bifurcation control in a fractional-order delayed predator–prey model. Phys. A 515, 183–191 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  42. Huang, C.D., Li, H., Cao, J.D.: A novel strategy of bifurcation control for a delayed fractional predator–prey model. Appl. Math. Comput. 347, 808–838 (2019)

    MathSciNet  MATH  Google Scholar 

  43. Deng, W., Li, C.: Synchronization of chaotic fractional Chen system. J. Phys. Soc. Jpn. 74(6), 1645–1648 (2005)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work was partially supported by Liaoning Provincial Department of Education Scientific Research Fund Project (lnjc202018). Authors are thankful to the editor and reviewers for their constructive suggestions and comments.

Author information

Authors and Affiliations

  1. College of sciences, Northeastern University, Shenyang, 110819, Liaoning, China

    Caihong Song & Ning Li

Authors
  1. Caihong Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ning Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors read and approved the final manuscript.

Corresponding author

Correspondence to Ning Li.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, C., Li, N. Dynamic analysis and bifurcation control of a fractional-order cassava mosaic disease model. J. Appl. Math. Comput. 69, 1705–1730 (2023). https://doi.org/10.1007/s12190-022-01809-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01809-9

Keywords

Mathematics Subject Classification