Skip to main content

Advertisement

Springer Nature Link
Log in

Initial and boundary value problem of fuzzy fractional-order nonlinear Volterra integro-differential equations

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

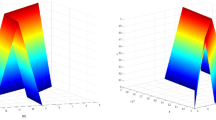
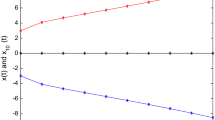
The fractional derivative in Caputo sense for the class of fuzzy fractional order Volterra integro-differential equations of the first kind is examined in this article. This paper considers both the initial and boundary value problems simultaneously. The transformation of first kind to second kind is done using Leibniz rule. Fixed point theory is used to establish the existence and uniqueness of the considered equation in its second kind. Furthermore, the Adomian decomposition method is used to determine the solution to the proposed problem. We provide some examples to back up the approach. The numerical and graphical representations of the symmetry between lower and upper cut representations of the fuzzy solutions are shown using MATLAB. A graphical representation is supported to critically examine how such methods work.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Miller, K.S., Ross, B.: An introduction to the fractional calculus and fractional differential equations. Wiley, New York (1993)

    MATH  Google Scholar 

  2. Podlubny, I.: Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier, Kosice (1998)

    MATH  Google Scholar 

  3. Arikoglu, A., Ozkol, I.: Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 34(5), 1473–1481 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  4. Ma, X., Huang, C.: Numerical solution of fractional integro-differential equations by a hybrid collocation method. Appl. Math. Comput. 219(12), 6750–6760 (2013)

    MathSciNet  MATH  Google Scholar 

  5. Jiang, W., Tian, T.: Numerical solution of nonlinear volterra integro-differential equations of fractional order by the reproducing kernel method. Appl. Math. Modell. 39(16), 4871–4876 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  6. Momani, S., Noor, M.A.: Numerical methods for fourth-order fractional integro-differential equations. Appl. Math. Comput. 182(1), 754–760 (2006)

    MathSciNet  MATH  Google Scholar 

  7. Zhu, L., Fan, Q.: Numerical solution of nonlinear fractional-order Volterra integro-differential equations by scw. Commun. Nonlinear Sci. Numer. Simul. 18(5), 1203–1213 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Sayevand, K.: Analytical treatment of Volterra integro-differential equations of fractional order. Appl. Math. Modell. 39(15), 4330–4336 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Linz, P.: Analytical and numerical methods for Volterra equations. SIAM, Philadelphia (1985)

    Book  MATH  Google Scholar 

  10. Wazwaz, A.-M.: Nonlinear volterra integro-differential equations. In: Linear and Nonlinear Integral Equations, pp. 425–465. Springer, Berlin, Heidelberg (2011)

  11. Das, P., Rana, S., Ramos, H.: On the approximate solutions of a class of fractional order nonlinear Volterra integro-differential initial value problems and boundary value problems of first kind and their convergence analysis. J. Comput. Appl. Math. 404, 113116 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chang, S.S., Zadeh, L.A.: On fuzzy mapping and control. In: Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh, pp. 180–184. World Scientific, Singapore (1996)

  13. Dubois, D., Prade, H.: Operations on fuzzy numbers. Int. J. Syst. Sci. 9(6), 613–626 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dubois, D., Prade, H.: Towards fuzzy differential calculus part 1: integration of fuzzy mappings. Fuzzy Sets Syst. 8(1), 1–17 (1982)

    Article  MATH  Google Scholar 

  15. Kaleva, O.: Fuzzy differential equations. Fuzzy Sets Syst 24(3), 301–317 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  16. Abbasbandy, S., Hashemi, M.: Fuzzy integro-differential equations: formulation and solution using the variational iteration method. Nonlinear Sci. Lett. A 1(4), 413–418 (2010)

    Google Scholar 

  17. Abbasbandy, S., Hashemi, M.: A series solution of fuzzy integrodifferential equations, J. of Fuzzy Set Valued Anal. 1, 413–418, (2010)

  18. Arqub, O.A.: Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm-Volterra integrodifferential equations. Neural Comput. Appl. 28(7), 1591–1610 (2017)

    Article  Google Scholar 

  19. Alaroud, M., Al-Smadi, M., Rozita Ahmad, R., Salma Din, U.K.: An analytical numerical method for solving fuzzy fractional Volterra integro-differential equations. Symmetry 11(2), 205 (2019)

    Article  MATH  Google Scholar 

  20. Agarwal, R.P., Lakshmikantham, V., Nieto, J.J.: On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal. Theory Methods Appl. 72(6), 2859–2862 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Shahriyar, M., Ismail, F., Aghabeigi, S., Ahmadian, A., Salahshour, S.: An eigenvalue-eigenvector method for solving a system of fractional differential equations with uncertainty, Mathe. Probl. Eng. 2013 (2013) https://doi.org/10.1155/2013/579761

  22. Miller, R.K., Sell, G.R.: Existence, uniqueness and continuity of solutions of integral equations. Annali di Matematica Pura ed Applicata 80(1), 135–152 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  23. Pachpatte, B.: On fredholm type integrodifferential equation. Tamkang J. Math. 39(1), 85–94 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  24. Matinfar, M., Ghanbari, M., Nuraei, R.: Numerical solution of linear fuzzy volterra integro-differential equations by variational iteration method. J. Intell. Fuzzy Syst. 24(3), 575–586 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  25. Padmapriya, V., Kaliyappan, M., Parthiban, V.: Solution of fuzzy fractional integro-differential equations using a domian decomposition method. J. Inf. Math. Sci. 9(3), 501–507 (2017)

    Google Scholar 

  26. Gumah, G., Moaddy, K., Al-Smadi, M., Hashim, I.: Solutions of uncertain Volterra integral equations by fitted reproducing kernel Hilbert space method J. Funct. Spaces, 2016 (2016), https://doi.org/10.1155/2016/2920463

  27. Shabestari, M.R.M., Ezzati, R., Allahviranloo, T.: Numerical solution of fuzzy fractional integro-differential equation via two-dimensional legendre wavelet method. J. Intell. Fuzzy Syst. 34(4), 2453–2465 (2018)

    Article  Google Scholar 

  28. Ahmad, N., Ullah, A., Ullah, A., Ahmad, S., Shah, K., Ahmad, I.: On analysis of the fuzzy fractional order Volterra-fredholm integro-differential equation. Alex. Eng. J. 60(1), 1827–1838 (2021)

    Article  Google Scholar 

  29. Abu Arqub, O., Singh, J., Maayah, B., Alhodaly, M.: “Reproducing kernel approach for numerical solutions of fuzzy fractional initial value problems under the Mittag–Leffler kernel differential operator,” Math. Methods Appl. Sci. 2021, 1–22, (2021)

  30. Abu Arqub, O., Singh, J.,Alhodaly, M.: Adaptation of kernel functions-based approach with Atangana-Baleanu-Caputo distributed order derivative for solutions of fuzzy fractional Volterra and Fredholm integrodifferential equations. Math Methods Appl Sci. (2021). https://doi.org/10.1002/mma.7228. (In press)

  31. Al-Smadi, M., Arqub, O.A.: Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 342, 280–294 (2019)

    MathSciNet  MATH  Google Scholar 

  32. Al-Smadi, M., Arqub, O.A., Zeidan, D.: Fuzzy fractional differential equations under the mittag-leffler kernel differential operator of the abc approach: Theorems and applications. Chaos Solitons Fractals 146, 110891 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. Al-Smadi, M., Dutta, H., Hasan, S., Momani, S.: On numerical approximation of atangana-baleanu-caputo fractional integro-differential equations under uncertainty in hilbert space. Math. Modell. Nat. Phenom. 16, 41 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  34. Adomian, G.: Solution of physical problems by decomposition. Comput. Math. Appl. 27(9–10), 145–154 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  35. Alshammari, M., Al-Smadi, M., Arqub, O.A., Hashim, I., Alias, M.A.: Residual series representation algorithm for solving fuzzy duffing oscillator equations. Symmetry 12(4), 572 (2020)

    Article  Google Scholar 

  36. Al-Smadi, M.: Fractional residual series for conformable time-fractional Sawada-Kotera-Ito, Lax, and Kaup-Kupershmidt equations of seventh order, Math. Methods Appl. Sci. (2021). https://doi.org/10.1002/mma.7507. (In press)

  37. Bede, B., Stefanini, L.: Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 230, 119–141 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  38. Haq, E.U., Hassan, Q.M.U., Ahmad, J., Ehsan, K.: Fuzzy solution of system of fuzzy fractional problems using a reliable method. Alex. Eng. J. 61(4), 3051–3058 (2022)

    Article  Google Scholar 

  39. Adomian, G., Rach, R.: Equality of partial solutions in the decomposition method for linear or nonlinear partial differential equations. Comput. Math. Appl. 19(12), 9–12 (1990)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Advanced Sciences, Vellore Institute of Technology, Chennai Campus, Chennai, Tamil Nadu, 600127, India

    K. Agilan & V. Parthiban

Authors
  1. K. Agilan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. V. Parthiban
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to K. Agilan.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Agilan, K., Parthiban, V. Initial and boundary value problem of fuzzy fractional-order nonlinear Volterra integro-differential equations. J. Appl. Math. Comput. 69, 1765–1793 (2023). https://doi.org/10.1007/s12190-022-01810-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01810-2

Keywords

Mathematics Subject Classification