Skip to main content

Advertisement

Springer Nature Link
Log in

Numerical solution of two-dimensional inverse time-fractional diffusion problem with non-local boundary condition using a-polynomials

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

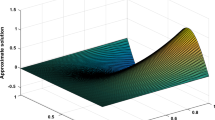
In this paper, we obtain the numerical solution of two-dimensional inverse time-fractional diffusion problem with non-local boundary condition using a-polynomials. These polynomials are equipped with an unknown parameter a that is obtained by collocation and least squares methods. In fact, the optimal parameter a is replaced in the a-polynomials, and then with these polynomials that no longer have the a parameter, the numerical solution is approximated. Time discretization of the equation is performed by \({L_1}\) method. The convergence theorem for a-polynomials has been proved in this article. In three examples, four types of measurement errors have been used to confirm the accuracy of the present method and compare the results with other methods. The stability of the present method has been investigated in all examples when the input data is contaminated with noise. Considering that in each example, the optimum value of parameter a is obtained, the results are stable in noise mode. The results in the examples also show the accuracy and advantage of the present method in comparison with the other method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Abbasbandy, S.: A new class of polynomial functions equipped with a parameter. Math. Sci. 11, 127–130 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ahmad, B., Alsaedi, A., Ntouyas, S.K., Tariboon, J.: Hadamard-Type Fractional Differential Equations, Inclusions and Inequalities. Springer, Switzerland (2017)

    Book  MATH  Google Scholar 

  3. Brociek, R., Słota, D., Zielonka, A.: Reconstruction robin boundary condition in the heat conduction inverse problem of fractional order. In: Theory and Applications of Non–Integer Order Systems, pp. 147–156 (2017)

  4. Bueno-Orovio, A., Kay, D., Grau, V., Rodriguez, B., Burrage, K.: Fractional diffusion models of cardiac electrical propagation: role of structural heterogeneity in dispersion of repolarization. J. R. Soc. Interface 11(97), 20140352 (2014)

    Article  Google Scholar 

  5. Can, N.H., Luc, N.H., Baleanu, D., Zhou, Y., Long, L.D.: Inverse source problem for time fractional diffusion equation with Mittag–Leffler kernel. Adv. Differ. Equ. 2020(1), 1–8 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  6. Cheng, H., Fu, C.L.: An iteration regularization for a time-fractional inverse diffusion problem. Appl. Math. Model. 36(11), 5642–5649 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Deü, J.F., Matignon, D.: Simulation of fractionally damped mechanical systems by means of a Newmark-diffusive scheme. Comput. Math. Appl. 59(5), 1745–1753 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Diethelm, K.: The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type. Springer, Heidelberg (2010)

    Book  MATH  Google Scholar 

  9. Djennadi, S., Shawagfeh, N., Arqub, O.A.: A fractional Tikhonov regularization method for an inverse backward and source problems in the time-space fractional diffusion equations. Chaos Solitons Fract. 150, 111127 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  10. Djennadi, S., Shawagfeh, N., Arqub, O.A.: A numerical algorithm in reproducing kernel-based approach for solving the inverse source problem of the time-space fractional diffusion equation. Part. Differ. Equ. Appl. Math. 4, 100164 (2021)

    MATH  Google Scholar 

  11. Djennadi, S., Shawagfeh, N., Arqub, O.A.: Well-posedness of the inverse problem of time fractional heat equation in the sense of the Atangana-Baleanu fractional approach. Alex. Eng. J. 59(4), 2261–2268 (2020)

    Article  Google Scholar 

  12. Djennadi, S., Shawagfeh, N., Osman, M.S., Gómez-Aguilar, J.F., Arqub, O.A.: The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique. Phys. Scr. 96(9), 094006 (2021)

    Article  Google Scholar 

  13. Feng, P., Karimov, E.T.: Inverse source problems for time-fractional mixed parabolic-hyperbolic-type equations. J. Inverse Ill-posed Problems 23(4), 339–353 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  14. Guo, B., Pu, X., Huang, F.: Fractional Partial Differential Equations and their Numerical Solutions. World Scientific Publishing Company, Beijing (2015)

    Book  MATH  Google Scholar 

  15. Guo, B.Y., Shen, J., Wang, Z.Q.: Chebyshev rational spectral and pseudospectral methods on a semi-infinite interval. Int. J. Numer. Meth. Engng 53, 65–84 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. Hajishafieiha, J., Abbasbandy, S.: A new method based on polynomials equipped with a parameter to solve two parabolic inverse problems with a nonlocal boundary condition. Inverse Problems Sci. Eng. 1, 1–15 (2019)

    MATH  Google Scholar 

  17. Hajishafieiha, J., Abbasbandy, S.: A new class of polynomial functions for approximate solution of generalized Benjamin–Bona–Mahony–Burgers (gBBMB) equations. Appl. Math. Comput. 367, 124765 (2020)

    MathSciNet  MATH  Google Scholar 

  18. Hanson, G.W., Yakovlev, A.B.: Operator Theory for Electromagnetics. Springer, New York (2002)

    Book  MATH  Google Scholar 

  19. Kirane, M., Malik, S.A., Al-Gwaiz, M.A.: An inverse source problem for a two dimensional time fractional diffusion equation with nonlocal boundary conditions. Math. Methods Appl. Sci. 36(9), 1056–1069 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Li, M., Xi, X.X., Xiong, X.T.: Regularization for a fractional sideways heat equation. J. Comput. Appl. Math. 255, 28–43 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Li, C., Zeng, F.: Numerical Methods for Fractional Calculus. Chapman and Hall/CRC, (2019)

  22. Liu, C.S., Chen, W., Fu, Z.: A multiple-scale MQ-RBF for solving the inverse Cauchy problems in arbitrary plane domain. Eng. Anal. Bound. Elem. 68, 11–16 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Liu, S., Feng, L.: An inverse problem for a two-dimensional time-fractional sideways heat equation. Math. Problems Eng. 1, 2020 (2020)

    MathSciNet  Google Scholar 

  24. Liu, Y., Rundell, W., Yamamoto, M.: Strong maximum principle for fractional diffusion equations and an application to an inverse source problem. Fract. Calc. Appl. Anal. 19(4), 888–906 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  25. Lopushanska, H., Rapita, V.: Inverse coefficient problem for the semi-linear fractional telegraph equation. Electron. J. Differ. Equ. 153, 1–13 (2015)

    MathSciNet  MATH  Google Scholar 

  26. Magin, R.L.: Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 59(5), 1586–1593 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  27. Milici, C., Drăgănescu, G., Machado, J.T.: Introduction to Fractional Differential Equations. Springer, Switzerland (2019)

    Book  MATH  Google Scholar 

  28. Mirkhezri, A.: MLPG method based on particular solution to identify a time-dependent boundary source for the time-fractional diffusion equation. Int. J. Comput. Math. 98(4), 657–670 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  29. Pao, C.V.: Reaction diffusion equations with nonlocal boundary and nonlocal initial conditions. J. Math. Anal. Appl. 195(3), 702–718 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  30. Povstenko, Y.: Fractional Thermoelasticity. Springer, New York (2015)

    Book  MATH  Google Scholar 

  31. Rassias, J.M., Karimov, E.T.: Boundary–value problems with non–local condition for degenerate parabolic equations. arXiv preprint arXiv:1301.3208 (2013)

  32. Ray, S.S.: Fractional Calculus with Applications for Nuclear Reactor Dynamics. Taylor & Francis Group, Boca Raton (2016)

    MATH  Google Scholar 

  33. Roohani Ghehsareh, H., Zabetzadeh, S.M.: A meshless computational approach for solving two-dimensional inverse time-fractional diffusion problem with non-local boundary condition. Inverse Problems Sci. Eng. 28(12), 1773–1795 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Ruan, Z., Zhang, S., Xiong, S.: Solving an inverse source problem for a time fractional diffusion equation by a modified quasi-boundary value method. Evol. Equ.Control Theory 7(4), 669 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  35. Šišková, K., Slodička, M.: Recognition of a time-dependent source in a time-fractional wave equation. Appl. Numer. Math. 121, 1–7 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  36. Slodička, M.: Determination of a solely time-dependent source in a semilinear parabolic problem by means of boundary measurements. J. Comput. Appl. Math. 289, 433–440 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  37. Uçar, S., Uçar, E., Özdemir, N., Hammouch, Z.: Mathematical analysis and numerical simulation for a smoking model with Atangana–Baleanu derivative. Chaos Solitons Fract. 118, 300–306 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  38. Wang, J.G., Zhou, Y.B., Wei, T.: Two regularization methods to identify a space-dependent source for the time-fractional diffusion equation. Appl. Numer. Math. 68, 39–57 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  39. Wei, T., Zhang, Z.Q.: Reconstruction of a time-dependent source term in a time-fractional diffusion equation. Eng. Anal. Boundary Elem. 37(1), 23–31 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  40. Xiong, X., Guo, H., Liu, X.: An inverse problem for a fractional diffusion equation. J. Comput. Appl. Math. 236(17), 4474–4484 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  41. Yan, L., Yang, F.: The method of approximate particular solutions for the time-fractional diffusion equation with a non-local boundary condition. Comput. Math. Appl. 70(3), 254–264 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zhang, Y., Xu, X.: Inverse source problem for a fractional diffusion equation. Inverse Prob. 27(3), 035010 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zheng, G.H., Wei, T.: Spectral regularization method for solving a time-fractional inverse diffusion problem. Appl. Math. Comput. 218(2), 396–405 (2011)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank the anonymous reviewers for helpful comments, which lead to definite improvement in the manuscript.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Imam Khomeini International University, 34149-16818, Qazvin, Iran

    Jalal Hajishafieiha & Saeid Abbasbandy

Authors
  1. Jalal Hajishafieiha
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Saeid Abbasbandy
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Saeid Abbasbandy.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hajishafieiha, J., Abbasbandy, S. Numerical solution of two-dimensional inverse time-fractional diffusion problem with non-local boundary condition using a-polynomials. J. Appl. Math. Comput. 69, 1945–1965 (2023). https://doi.org/10.1007/s12190-022-01812-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01812-0

Keywords

Mathamatics Subject Classification