Skip to main content

Advertisement

Springer Nature Link
Log in

Analysis of finite difference schemes for Volterra integro-differential equations involving arbitrary order derivatives

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

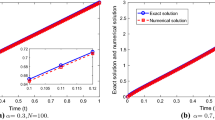
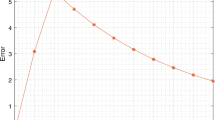
In this work, we consider a Volterra integro-differential equation involving Caputo fractional derivative of order \( \alpha \in (0,1). \) To approximate the solution, we propose two finite difference schemes that use L1 and L1-2 discretization to approximate the differential part and a composite trapezoidal rule to approximate an integral part. The error estimates for both schemes are established. It is shown that the approximate solution obtained by using the L1-2 scheme converges to the exact solution more rapidly than the L1 scheme. Finally, some numerical experiments are carried out to show the validity and accuracy of the proposed schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availibility

The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Amirali, I., Acar, H.: A novel approach for the stability inequalities for high-order Volterra delay integro-differential equation. J. Appl. Math. Comput. (2022). https://doi.org/10.1007/s12190-022-01761-8

    Article  Google Scholar 

  2. Carpinteri, A., Chiaia, B., Cornetti, P.: Static-kinematic duality and the principle of virtual work in the mechanics of fractal media. Comput. Methods Appl. Mech. Eng. 191, 3–19 (2001)

    Article  MATH  Google Scholar 

  3. Diethelm, K.: The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type, vol. 2004. Springer, Berlin (2010)

    MATH  Google Scholar 

  4. Gao, G.H., Sun, Z.Z., Zhang, H.W.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  5. Gordji, M.E., Baghani, H., Baghani, O.: On existence and uniqueness of solutions of a nonlinear integral equation. J. Appl. Math. (2011). https://doi.org/10.1155/2011/743923

    Article  MathSciNet  MATH  Google Scholar 

  6. Hamoud, A.A., Ghadle, K.P., Issa, M.B., Giniswamy, H.: Existence and uniqueness theorems for fractional Volterra-Fredholm integro-differential equations. Int. J. Appl. Math. 31(3), 333–348 (2018)

    Article  MathSciNet  Google Scholar 

  7. Hamoud, A.A., Ghadle, K.P.: Some new existence, uniqueness and convergence results for fractional Volterra-Fredholm integro-differential equations. J. Appl. Comput. Mech. 5(1), 58–69 (2019)

    Google Scholar 

  8. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, San Diego (2006)

    MATH  Google Scholar 

  9. Larsson, S., Racheva, M., Saedpanah, F.: Discontinuous Galerkin method for an integro-differential equation modeling dynamic fractional order viscoelasticity, Comput. Methods. Appl. Mech. Eng. 283, 196–209 (2015)

    Article  MATH  Google Scholar 

  10. Lepik, U.: Solving fractional integral equations by the Haar wavelet method. Appl. Math. Comput. 214(2), 468–478 (2009)

    MathSciNet  MATH  Google Scholar 

  11. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225(2), 1533–1552 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Momani, S.M.: Local and global existence theorems on fractional integro-differential equations. J. Fract. Calc. 18, 81–86 (2000)

    MathSciNet  MATH  Google Scholar 

  13. Momani, S., Noor, M.A.: Numerical methods for fourth-order fractional integro-differential equations. Appl. Math. Comput. 182(1), 754–760 (2006)

    MathSciNet  MATH  Google Scholar 

  14. Panda, A., Santra, S., Mohapatra, J.: Adomian decomposition and homotopy perturbation method for the solution of time fractional partial integro-differential equations. J. Appl. Math. Comput. (2021). https://doi.org/10.1007/s12190-021-01613-x

    Article  MATH  Google Scholar 

  15. Panda, A., Mohapatra, J., Amirali, I.: A second-order post-processing technique for singularly perturbed volterra integro-differential equations. Mediterr. J. Math. 18(6), 1–25 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  16. Podlubny, I.: Fractional Differential Equations. Academie Press, New York (1999)

    MATH  Google Scholar 

  17. Rawashdeh, E.A.: Numerical solution of fractional integro-differential equations by collocation method. Appl. Math. Comput. 176, 1–6 (2006)

    MathSciNet  MATH  Google Scholar 

  18. Santra, S., Mohapatra, J.: Numerical analysis of Volterra integro-differential equations with Caputo fractional derivative. Iran. J. Sci. Technol. Trans. Sci. 45, 1815–1824 (2021)

    Article  MathSciNet  Google Scholar 

  19. Santra, S., Mohapatra, J.: A novel finite difference technique with error estimate for time fractional partial integro-differential equation of Volterra type. J. Comput. Appl. Math. (2021). https://doi.org/10.1016/j.cam.2021.113746

    Article  MATH  Google Scholar 

  20. Santra, S., Panda, A., Mohapatra, J.: A novel approach for solving multi-term time fractional Volterra-Fredholm partial integro-differential equations. J. Appl. Math. Comput. (2021). https://doi.org/10.1007/s12190-021-01675-x

    Article  MATH  Google Scholar 

  21. Sayevand, K., Fardi, M., Moradi, E., Boroujeni, F.H.: Convergence analysis of homotopy perturbation method for Volterra integro-differential equations of fractional order. Alex. Eng. J. 52, 807–812 (2013)

    Article  Google Scholar 

  22. Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55(2), 1057–1079 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Wongyat, T., Sintunavarat, W.: The existence and uniqueness of the solution for nonlinear Fredholm and Volterra integral equations together with nonlinear fractional differential equations via w-distances. Adv. Differ. Equ. 1, 211 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Yapman, Ö., Amiraliyev, G.M., Amirali, I.: Convergence analysis of fitted numerical method for a singularly perturbed nonlinear Volterra integro-differential equation with delay. J. Comput. Appl. Math. 355, 301–309 (2019). https://doi.org/10.1016/j.cam.2019.01.026

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author would like to thank the Council of Scientific & Industrial Research (CSIR), Government of India (File No.: 09/983(0046)/2020-EMR-I), for financial support to carry out his research work at NIT Rourkela.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Rourkela, Rourkela, Odisha, 769008, India

    Bappa Ghosh & Jugal Mohapatra

Authors
  1. Bappa Ghosh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jugal Mohapatra
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jugal Mohapatra.

Ethics declarations

Conflict of interest

The authors declare that there is no conflicts of interest.

Informed consent

On behalf of the authors, Dr. Jugal Mohapatra shall be communicating the manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghosh, B., Mohapatra, J. Analysis of finite difference schemes for Volterra integro-differential equations involving arbitrary order derivatives. J. Appl. Math. Comput. 69, 1865–1886 (2023). https://doi.org/10.1007/s12190-022-01817-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01817-9

Keywords

Mathematics Subject Classification