Skip to main content

Advertisement

Springer Nature Link
Log in

Existence, uniqueness and stability of positive periodic solutions for an iterative Nicholson’s blowflies equation

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

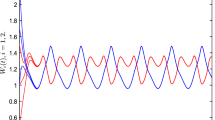
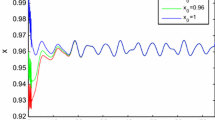
The main motive and, at the same time, the goal of this work is to investigate a revisited Nicholson’s blowflies equation that involves a time varying delay and an iterative term. We make use of Schauder’s fixed point theorem to tackle the existence of positive periodic solutions and under an additional condition, we apply the Banach contraction principle for establishing the existence, uniqueness and stability results. Finally, we give two examples to illustrate the effectiveness of our main results that are completely new and complement some earlier investigations to some extent.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Not applicable.

References

  1. Bouakkaz, A.: Bounded solutions to a three-point fourth-order iterative boundary value problem. Rocky Mt. J. Math. 52(3), 793–803 (2022). https://doi.org/10.1216/rmj.2022.52.793

    Article  MathSciNet  MATH  Google Scholar 

  2. Bouakkaz, A.: Positive periodic solutions for a class of first-order iterative differential equations with an application to a hematopoiesis model. Carpathian J. Math. 38(2), 347–355 (2022). https://doi.org/10.37193/CJM.2022.02.07

    Article  MathSciNet  Google Scholar 

  3. Bouakkaz, A., Khemis, R.: Positive periodic solutions for a class of second-order differential equations with state dependent delays. Turkish J. Math. 44(4), 1412–1426 (2020). https://doi.org/10.3906/mat-2004-52

    Article  MathSciNet  MATH  Google Scholar 

  4. Bouakkaz, A., Khemis, R.: Positive periodic solutions for revisited Nicholson’s blowflies equation with iterative harvesting term. J. Math. Anal. Appl. 494(2), 124663 (2021). https://doi.org/10.1016/j.jmaa.2020.124663

    Article  MathSciNet  MATH  Google Scholar 

  5. Cheraiet, S., Bouakkaz, A., Khemis, R.: Bounded positive solutions of an iterative three-point boundary-value problem with integral boundary conditions. J. Appl. Math. Comput. 65, 597–610 (2021). https://doi.org/10.1007/s12190-020-01406-8

    Article  MathSciNet  MATH  Google Scholar 

  6. Cheraiet, S., Bouakkaz, A., Khemis, R.: Some new findings on bounded solution of a third order iterative boundary-value problem. J. Interdiscip. Math. 25(4), 1153–1162 (2022). https://doi.org/10.1080/09720502.2021.1995215

    Article  Google Scholar 

  7. Chouaf, S., Bouakkaz, A., Khemis, R.: On bounded solutions of a second-order iterative boundary value problem. Turkish J. Math. 46(2), 453–464 (2022). https://doi.org/10.3906/mat-2106-45

    Article  MathSciNet  MATH  Google Scholar 

  8. Chouaf, S., Khemis, R., Bouakkaz, A.: Some existence results on positive solutions for an iterative second-order boundary-value problem with integral boundary conditions. Bol. Soc. Parana. Mat. 3(40), 1–10 (2022). https://doi.org/10.5269/bspm.52461

    Article  MathSciNet  MATH  Google Scholar 

  9. Fečkan, M., Wang, J., Zhao, H.Y.: Maximal and minimal nondecreasing bounded solutions of iterative functional differential equations. Appl. Math. Lett. 113, 106886 (2021). https://doi.org/10.1016/j.aml.2020.106886

    Article  MathSciNet  MATH  Google Scholar 

  10. Gurney, W., Blythe, S., Nisbet, R.: Nicholson’s blowflies revisited. Nature 287, 17–21 (1980). https://doi.org/10.1038/287017a0

    Article  Google Scholar 

  11. Huang, C., Yang, X., Cao, J.: Stability analysis of Nicholson’s blowflies equation with two different delays. Math. Comput. Simul. 171(9), 201–206 (2020). https://doi.org/10.1016/j.matcom.2019.09.023

    Article  MathSciNet  MATH  Google Scholar 

  12. Khemis, M., Bouakkaz, A.: Existence, uniqueness and stability results of an iterative survival model of red blood cells with a delayed nonlinear harvesting term. J. Math. Model. 10(3), 515–528 (2022). https://doi.org/10.22124/JMM.2022.21577.1892

    Article  MathSciNet  Google Scholar 

  13. Khemis, R., Ardjouni, A., Bouakkaz, A., Djoudi, A.: Periodic solutions of a class of third-order differential equations with two delays depending on time and state. Comment. Math. Univ. Carolin. 60(3), 379–399 (2019). https://doi.org/10.14712/1213-7243.2019.018

    Article  MathSciNet  MATH  Google Scholar 

  14. Khuddush, M., Prasad, K.R.: Nonlinear two-point iterative functional boundary value problems on time scales. J. Appl. Math. Comput. (2022). https://doi.org/10.1007/s12190-022-01703-4

    Article  MathSciNet  MATH  Google Scholar 

  15. Long, X., Gong, S.: New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 100, 106027 (2020). https://doi.org/10.1016/j.aml.2019.106027

    Article  MathSciNet  MATH  Google Scholar 

  16. Mezghiche, L., Khemis, R., Bouakkaz, A.: Positive periodic solutions for a neutral differential equation with iterative terms arising in biology and population dynamics. Int. J. Nonlinear Anal. Appl. (2022). https://doi.org/10.22075/IJNAA.2022.26264.3281

  17. Xu, C., Liao, M., Li, P., Guo, Y., Liu, Z.: Bifurcation properties for fractional order delayed BAM neural networks. Cogn. Comput. 13, 322–356 (2021). https://doi.org/10.1007/s12559-020-09782-w

    Article  Google Scholar 

  18. Xu, C., Liao, M., Li, P., Xiao, Q., Yuan, S.: A new method to investigate almost periodic solutions for an Nicholson’s blowflies model with time-varying delays and a linear harvesting term. Math. Biosci. Eng. 16(5), 3830–3840 (2019). https://doi.org/10.3934/mbe.2019189

    Article  MathSciNet  MATH  Google Scholar 

  19. Xu, C., Liao, M., Pang, Y.: Existence and convergence dynamics of pseudo almost periodic solutions for Nicholson’s blowflies model with time-varying delays and a harvesting term. Acta Appl. Math. 146, 95–112 (2016). https://doi.org/10.1007/s10440-016-0060-7

    Article  MathSciNet  MATH  Google Scholar 

  20. Xu, C., Li, P., Yuan, S.: New findings on exponential convergence of a Nicholson’s blowflies model with proportional delay. Adv. Differ. Equ. 2019, 358 (2019). https://doi.org/10.1186/s13662-019-2248-4

    Article  MathSciNet  MATH  Google Scholar 

  21. Xu, C., Liu, Z., Aouiti, C., Li, P., Yao, L., Yan, J.: New exploration on bifurcation for fractional-order quaternion-valued neural networks involving leakage delays. Cogn. Neurodyn. 16, 1233–1248 (2022). https://doi.org/10.1007/s11571-021-09763-1

    Article  Google Scholar 

  22. Xu, C., Zhang, W., Aouiti, C., Liu, Z., Yao, L.: Further analysis on dynamical properties of fractional-order bi-directional associative memory neural networks involving double delays. Math. Methods Appl. Sci. (2022). https://doi.org/10.1002/mma.8477

    Article  MathSciNet  Google Scholar 

  23. Zhao, H.Y., Fečkan, M.: Periodic solutions for a class of differential equations with delays depending on state. Math. Commun. 23, 29–42 (2018)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Applied Mathematics and History and Didactics of Mathematics (LAMAHIS), University of 20 August 1955, Skikda, Algeria

    Rabah Khemis

Authors
  1. Rabah Khemis
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Rabah Khemis.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khemis, R. Existence, uniqueness and stability of positive periodic solutions for an iterative Nicholson’s blowflies equation. J. Appl. Math. Comput. 69, 1903–1916 (2023). https://doi.org/10.1007/s12190-022-01820-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01820-0

Keywords

Mathematics Subject Classification