Skip to main content

Advertisement

Springer Nature Link
Log in

A hybrid BB-type method for solving large scale unconstrained optimization

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

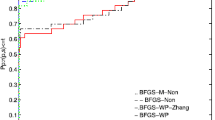
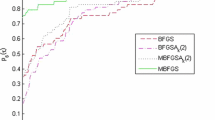
Abstract

In this paper, based on the ideas of Barzilai and Borwein (BB) method and IMPBOT algorithm proposed by Brown and Biggs (J Optim Theory Appl 62:211–224, 1989), we propose a hybrid BB-type method with a nonmonotone line search for solving large scale unconstrained optimization problems. Under mild conditions, the global convergence of the proposed method is analyzed. Numerical testing results and related comparisons are also reported to show the efficiency and robustness of the proposed hybrid method, especially for highly nonlinear optimization problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Bottou, L., Curtis, F.E., Nocedal, J.: Optimization methods for large-scale machine learning. SIAM Rev. 62, 223–311 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  2. Jiang, X.Z., Liao, W., Yin, J.H., Jian, J.B.: A new family of hybrid three-term conjugate gradient methods with applications in image restoration. Numer. Algorithms 91, 161–191 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  3. Liu, Y.F., Zhu, Z.B., Zhang, B.X.: Two sufficient descent three-term conjugate gradient methods for unconstrained optimization problems with applications in compressive sensing. J. Appl. Math. Comput. 68, 1787–1816 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  4. Barzilai, J., Borwein, J.M.: Two point step size gradient method. IMA J. Numer. Anal. 8, 141–148 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  5. Raydan, M.: The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem. SIAM J. Optim. 7, 26–33 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  6. Grippo, L., Lampariello, F., Lucidi, S.: A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 23, 707–716 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  7. Xiao, Y.H., Wang, Q.Y., Wang, D.: Notes on the Dai-Yuan-Yuan modified spectral gradient method. J. Comput. Appl. Math. 234, 2986–2992 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Cruz, W., Noguera, G.: Hybrid spectral gradient method for the unconstrained minimization problem. J. Glob. Optim. 44, 193–212 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Biglari, F., Solimanpur, M.: Scaling on the spectral gradient method. J. Optim. Theory Appl. 158, 626–635 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Arzani, F., Reza Peyghami, M.: A new nonmonotone filter Barzilai–Borwein method for solving unconstrained optimization problems. Int. J. Comput. Math. 93, 596–608 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  11. Lakhbab, H., Bernoussi, S.E.: Hybrid nonmonotone spectral gradient method for the unconstrained minimization problem. Comput. Appl. Math. 36, 1421–1430 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  12. Dai, Y.H., Huang, Y.K., Liu, X.W.: A family of spectral gradient methods for optimization. Comput. Optim. Appl. 74, 43–65 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  13. Sim, H.S., Chen, C.Y., Leong, W.J., Li, J.: Nonmonotone spectral gradient method based on memoryless symmetric rank-one update for large-scale unconstrained optimization. J. Ind. Manag. Optim. (2021), Published online, https://doi.org/10.3934/jimo.2021143

  14. Serafino, D., Ruggiero, V., Toraldo, G., Zanni, L.: On the steplength selection in gradient methods for unconstrained optimization. Appl. Math. Comput. 318, 176–195 (2018)

    MathSciNet  MATH  Google Scholar 

  15. Liu, Z.X., Liu, H.W.: An efficient gradient method with approximate optimal stepsize for large-scale unconstrained optimization. Numer. Algorithms 78, 21–39 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Liu, Z.X., Chu, W.L., Liu, H.W., Liu, Z.: An efficient gradient method with approximately optimal stepsizes based on regularization models for unconstrained optimization. RAIRO Oper. Res. 56, 2403–2424 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  17. Dai, Y.H., Kou, C.X.: A Barzilai–Borwein conjugate gradient method. Sci. China Math. 59, 1511–1524 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Sun, C., Zhang, Y.: A brief review on gradient method. Oper. Res. Trans. 25, 119–132 (2021)

    MathSciNet  Google Scholar 

  19. Brown, A.A., Biggs, M.C.: Some effective methods for unconstrained optimization based on the solution of system of ordinary differentiable equations. J. Optim. Theory Appl. 62, 211–224 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  20. Liao, L.Z., Qi, H.D., Qi, L.Q.: Neurodynamical optimization. J. Glob. Optim. 28, 175–195 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  21. Han, L.X.: On the convergence properties of an ODE algorithm for unconstrained optimization. Math. Numer. Sin. 15, 449–455 (1993)

    MathSciNet  MATH  Google Scholar 

  22. Higham, D.J.: Trust region algorithms and timestep selection. SIAM J. Numer. Anal. 37, 194–210 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  23. Zhang, L.H., Kelley, C.T., Liao, L.Z.: A continuous Newton-type method for unconstrained optimization. Pac. J. Optim. 4, 257–277 (2008)

    MathSciNet  MATH  Google Scholar 

  24. Luo, X.L., Kelley, C.T., Liao, L.Z., Tam, H.W.: Combining trust-region techniques and Rosenbrock methods to compute stationary points. J. Optim. Theory Appl. 140, 265–286 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ou, Y.G., Liu, Y.Y.: An ODE-based nonmonotone method for unconstrained optimization problems. J. Appl. Math. Comput. 42, 351–369 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  26. Ou, Y.G.: A hybrid trust region algorithm for unconstrained optimization. Appl. Numer. Math. 61, 900–909 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Chen, J., Qi, L.Q.: Pseudotransient continuation for solving systems of nonsmooth equations with inequality constraints. J. Optim. Theory Appl. 147, 223–242 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, L., Li, Y., Zhang, L.W.: A differential equation method for solving box constrained variational inequality problems. J. Ind. Manag. Optim. 7, 183–198 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Kelley, C.T., Liao, L.Z.: Explicit pseudo-transient continuation. Pac. J. Optim. 9, 77–91 (2013)

    MathSciNet  MATH  Google Scholar 

  30. Luo, X.L., Xiao, H., Lv, J.H.: Continuation Newton methods with the residual trust-region time-stepping scheme for nonlinear equations. Numer. Algorithms (2021), Published online https://doi.org/10.1007/s11075-021-01112-x

  31. Tan, Z.Z., Hu, R., Fang, Y.P.: A new method for solving split equality problems via projection dynamical systems. Numer. Algorithms 86, 1705–1719 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  32. Luo, X.L., Xiao, H., Lv, J.H., Zhang, S.: Explicit pseudo-transient continuation and the trust-region updating strategy for unconstrained optimization. Appl. Numer. Math. 165, 290–302 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. Sun, W.Y., Yuan, Y.X.: Optimization Theory and Methods: Nonlinear Programming. Springer Optimization and its Applications, vol. 1. Springer, New York, (2006)

  34. Wei, Z.X., Li, G.Y., Qi, L.Q.: New quasi-Newton methods for unconstrained optimization problems. Appl. Math. Comput. 175, 1156–1188 (2006)

    MathSciNet  MATH  Google Scholar 

  35. Zhang, J.Z., Deng, N.Y., Chen, L.H.: New quasi-Newton equation and related methods for unconstrained optimization. J. Optim. Theory Appl. 102, 147–167 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  36. Li, D.H., Fukushima, M.: A modified BFGS method and its global convergence in nonconvex minimization. J. Comput. Appl. Math. 129, 15–35 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  37. Babaie-Kafaki, S.: A modified BFGS algorithm based on a hybrid secant equation. Sci. China Math. 54, 2019–2036 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  38. Gu, N.Z., Mo, J.T.: Incorporating nonmonotone strategies into the trust region method for unconstrained optimization. Comput. Math. Appl. 55, 2158–2172 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zhang, H.C., Hager, W.W.: A nonmonotone line search technique and its applications to unconstrained optimization. SIAM J. Optim. 14, 1043–1056 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  40. Hager, W.W., Zhang, H.C.: A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J. Optim. 16, 170–192 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  41. Andrei, N.: An unconstrained optimization test functions collection. Adv. Model. Optim. 10, 147–161 (2008)

    MathSciNet  MATH  Google Scholar 

  42. Gould, N.I.M., Orban, D., Toint, P.L.: CUTEr: A constrained and unconstrained testing environment, revised. Trans. Math. Softw. 29, 373–394 (2003)

    Article  MATH  Google Scholar 

  43. Dolan, E.D., More, J.J.: Benchmarking optimization software with performance profiles. Math. Program. Ser. A 91, 201–213 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees and the associate editor for their careful reading of our manuscript and their valuable comments and constructive suggestions that greatly improved this manuscript’s quality.

Funding

This work is supported by NNSF of China (Nos.11961018, 12261028), STSF of Hainan Province (No. ZDYF2021SHFZ231), and Innovative Project for Postgraduates of Hainan Province (No. Qhys2021-207).

Author information

Authors and Affiliations

  1. Department of Mathematics, Hainan University, Haikou, 570228, Hainan, China

    Jian Gao & Yigui Ou

  2. Key Laboratory of Engineering Modeling and Statistical Computation of Hainan Province, Haikou, 570228, Hainan, China

    Yigui Ou

Authors
  1. Jian Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yigui Ou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yigui Ou.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file 1 (pdf 327 KB)

Appendices

Appendix 1

See Table 8.

Table 8 Numerical results
Full size table

Appendix 2

See Table 9.

Table 9 Appendix 2. Numerical results
Full size table

Appendix 3

See Table 10.

Table 10 Numerical results
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, J., Ou, Y. A hybrid BB-type method for solving large scale unconstrained optimization. J. Appl. Math. Comput. 69, 2105–2133 (2023). https://doi.org/10.1007/s12190-022-01826-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01826-8

Keywords

Mathematics Subject Classification