Skip to main content
Springer Nature Link
Log in

Qualitative behavior of exponential type of fuzzy difference equations system

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

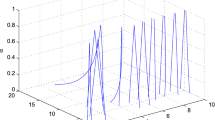
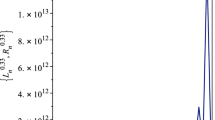Abstract

In this paper, we study the existence, uniqueness, and qualitative behavior of the fuzzy positive solutions to the following exponential type non-linear system of fuzzy difference equations with second-order.

$$\begin{aligned} x_{n+1}=\frac{\alpha _{1}+\beta _{1}e^{-x_{n-1}}}{\gamma _{1}+y_{n}},&\quad y_{n+1}=\frac{\alpha _{2}+\beta _{2}e^{-y_{n-1}}}{\gamma _{2}+x_{n}}, \quad n\in {\mathbb {N}}_{0}, \end{aligned}$$

where \(\alpha _{1},\alpha _{2}, \beta _{1},\beta _{2}, \gamma _{1}, \gamma _{2}\) are positive fuzzy numbers with the \(x_{-i},y_{-i},i \in \{0,1\},\) the fuzzy initial conditions. Also we give some numerical applications to support the theoretical aspects of the results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Shabbir, M.S., Din, Q., Safeer, M., Khan, M.A., Ahmad, K.: A dynamically consistent nonstandard finite difference scheme for a predator-prey model. Adv. Difference Equ. 1, 1–17 (2019)

    MathSciNet  Google Scholar 

  2. Gümüş, Ö.A.: Neimark-Sacker bifurcation and stability of a prey-predator system. Miskolc Math. Notes 21(2), 873–885 (2020)

    Article  MathSciNet  Google Scholar 

  3. Gümüş, Ö.A.: Bifurcation analysis and chaos control of discrete-time prey-predator model with Allee effect. Hacettepe J. Math. Statistics, 1-17

  4. Ozturk, I., Bozkurt, F., Ozen, S.: On the difference equation \(x_{n+1}=\frac{\alpha _{1}+\alpha _{2}e^{-x_{n}}}{\alpha _{3}+x_{n-1}}\). Appl. Math. Comput. 181, 1387–1393 (2006)

    MathSciNet  Google Scholar 

  5. Din, Q., Khan, K.A., Nosheen, A.: Stability analysis of a system of exponential difference equations. Discrete Dyn. Nat. Soc. 2014, 11 (2014)

    Article  MathSciNet  Google Scholar 

  6. Tran, T.H., Nguyen, A.D., Pham, T.A.: Global dynamics of some system of second-order difference equations. Electr. Res. Archive 29(6), 4159–4175 (2021)

    Article  MathSciNet  Google Scholar 

  7. Zadeh, L.A.: Fuzzy sets. Inf. Control 8, 338–353 (1965)

    Article  Google Scholar 

  8. Dubois, D., Prade, H.: Operations on fuzzy numbers. Int. J. Syst. Sci. 9(6), 613–626 (1978)

    Article  MathSciNet  Google Scholar 

  9. Stefanini, L.: A generalization of Hukuhara difference and division for interval and fuzzy arithmetic. Fuzzy Sets Syst. 161, 1564–1584 (2010)

    Article  MathSciNet  Google Scholar 

  10. Papaschinopoulos, G., Papadopoulos, B.K.: On the fuzzy difference equation \(x_{n+1}=A +\frac{x_{n}}{x_{n-m}}\). Fuzzy Sets Syst. 129, 73–81 (2002)

    Article  Google Scholar 

  11. Stefanidou, G., Papaschinopoulos, G., Schinas, C.: On an exponential-type fuzzy difference equation. Adv Differ Equ. 1–9, 196920 (2010)

    Article  MathSciNet  Google Scholar 

  12. Wang, C., Su, X., Liu, P., Hu, X., Li, R.: On the dynamics of a five-order fuzzy difference equation. J. Nonlinear Sci. Appl. 10, 3303–3319 (2017)

    Article  MathSciNet  Google Scholar 

  13. Khastan, A., Alijani, Z.: On the new solutions to the fuzzy difference equation xn+1=A +B/xn. Fuzzy Sets Syst. 358, 64–83 (2019)

    Article  Google Scholar 

  14. Zhang, Q., Liu, J., Luo, Z.: Dynamical behavior of a system of third-order rational difference equation. Discrete Dyn. Nat. Soc. 2015, 1–6 (2015)

    MathSciNet  Google Scholar 

  15. Zhang, Q., Liu, J., Luo, Z.: Dynamical behaviour of a third-order rational fuzzy difference equation. Adv. Differ. Equ. 2015, 1 (2015)

    Google Scholar 

  16. Zhang, Q., Yang, L., Liao, D.: On first order fuzzy Riccati difference equation. Inf. Sci. 270, 226–236 (2014)

    Article  Google Scholar 

  17. Zhang, Q., Yang, L., Liu, J.: Dynamics of a system of rational third-order difference equation. Adv. Differ. Equ., 1 (2012)

  18. Caihong, H., Lue, L., Guangwang, S., Taixiang, S.: Dynamical behaviors of a k-order fuzzy difference equation. Open Math. 20(1), 391–403 (2022)

    Article  MathSciNet  Google Scholar 

  19. Zhang, Q., Ouyang, M., Pan, B.: Qualitative analysis of second-order fuzzy difference equation with quadratic term. J. Appl. Math. Comput 69(2), 1355–1376 (2022)

    Article  MathSciNet  Google Scholar 

  20. Zhang, Q., Zhang, W., Lin, F., Li, D.: On dynamic behavior of second-order exponential-type fuzzy difference equation. Fuzzy Sets Syst. 419, 169–187 (2021)

    Article  MathSciNet  Google Scholar 

  21. El-Metwally, H., Grove, E.A., Ladas, G., Levins, R., Radin, M.: On the difference equation \(x_{n+1}=\alpha +\beta x_{n-1}e^{-x_{n}}\). Nonlinear Anal. 47(7), 4623–4634 (2001)

    Article  MathSciNet  Google Scholar 

  22. Ibrahim, T.F., Khan, A.Q.: Behavior of an exponential difference equations system. Math. Meth. Appl. Sci., 1- 13 (2023)

  23. Lu, J., Zhu, L., Gao, W.: Remarks on bipolar cubic fuzzy graphs and its chemical applications. Int. J. Math. Comput. Eng. 1(1), 3923 (2023)

    Article  Google Scholar 

  24. Kaleva, O., Seikkala, S.: On fuzzy metric spaces. Fuzzy Sets Syst. 12, 215–229 (1984)

    Article  Google Scholar 

  25. Tripathy, B.K., Nanda, S.: Absolute value of fuzzy real numbers and fuzzy sequence spaces. J. Fuzzy Math. 8(4), 883–892 (2000)

    MathSciNet  Google Scholar 

  26. Puri, M.L., Ralescu, D.A.: Differentials for fuzzy functions. J. Math. Anal. Appl. 91, 552–558 (1983)

    Article  MathSciNet  Google Scholar 

  27. Goetschel, J., Voxman, W.: Elementary fuzzy calculus. Fuzzy Sets Syst. 18(1), 31–43 (1986)

    Article  MathSciNet  Google Scholar 

  28. Bede, B.: Mathematics of fuzzy sets and fuzzy logic, Studies in Fuzziness and Soft Computing. Springer, Heidelberg (2013)

    Book  Google Scholar 

  29. Papaschinopoulos, G., Papadopoulos, B.K.: On the fuzzy diference equation \(x_{n+1}=A +\frac{B}{x_{n}}\). Soft. Comput. 6(6), 456–461 (2002)

    Article  Google Scholar 

  30. Zhang, Q., Lin, F., Zhong, X.: Asymptotic Behavior of Discrete Time Fuzzy Single Species Model, Discrete Dynamics in Nature and Society, Hindawi, 1-9 (2019)

  31. Dubois, D., Prade, H.: Possibility Theory: An Approach to Computerized Processing of Uncertainty. Plenum Publishing Corporation, New York (1998)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematics Department, Nevsehir Haci Bektas Veli University, Nevşehir, Turkey

    Sevda Atpinar & Yasin Yazlik

Authors
  1. Sevda Atpinar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yasin Yazlik
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sevda Atpinar.

Ethics declarations

Conflict of interest

The authors have no conflicts of interest to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Atpinar, S., Yazlik, Y. Qualitative behavior of exponential type of fuzzy difference equations system. J. Appl. Math. Comput. 69, 4135–4162 (2023). https://doi.org/10.1007/s12190-023-01919-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-023-01919-y

Keywords

Mathematics Subject Classification