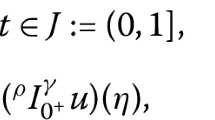Analysis on a nonlinear fractional differential equations in a bounded domain $[1,\mathcal {T}]$

Abstract

In this manuscript, based on the most widespread fixed point theories in literature. The existence of solutions to the system of nonlinear fractional differential equations with Caputo Hadmard fractional operator in a bounded domain is verified by using Mönoch’s fixed point theorem, The stability of the coupled system is also investigated via Ulam-Hyer technique. Finally, an applied numerical example is presented to illustrate the theoretical results obtained.

1 Introduction

Fractional calculus is a mathematical field extending the traditional concept of calculus to non-integer orders. It provides a powerful tool for modeling systems with complex dynamics that cannot be adequately described using integer-order derivatives alone. This branch of mathematics is characterized by its ability to handle irregularities and complexities in various phenomena, making it particularly useful in disciplines like physics, engineering see [1,2,3,4],and [8], for example in thermodynamics analysis of hydromagnetic convection in a channel, in [12] the authors studied impacts of fraction calculus on the MHD analysis of an incompressible fluid flow with entropy generation, viscous dissipation, and joule heating carried out between two endless vertical plates. In [13] the authors focuses on fractional-order derivatives for the unsteady flow of magnetohydrodynamic (MHD) methanol-iron oxide (CH3OH–Fe3O4) nanofluid over a permeable vertical plate.For more practical applications of fractional differentiation, the reader can refer to [14,15,16].

Fractional calculus offers a more comprehensive approach for studying processes with memory and hereditary properties, where the effects of past states influence current behavior, see [9,10,11]. The flexibility and broad applicability of fractional calculus have led to a growing interest in its theoretical development and practical applications across diverse scientific and engineering domains, see [20,21,22].

Fixed point theorems play a crucial role in the study of fractional differential equations, providing essential theoretical underpinnings for analyzing and solving these equations. These theorems, which establish conditions under which a function will have a point that maps to itself, are particularly valuable in the realm of fractional calculus, see [17,18,19]. They are used to ascertain the existence and uniqueness of solutions to fractional differential equations, a key aspect in many applied sciences. This approach is especially beneficial when dealing with nonlinear fractional differential equations, where traditional methods might fall short, see [23,24,25,26]. Fixed point theorems thus serve as a foundational tool in both the qualitative and quantitative analysis of fractional systems, aiding in the exploration of complex dynamical behaviors in fields ranging from engineering to biophysics, see [27,28,29,30]. Their application helps to unravel solutions in situations where conventional calculus does not provide adequate answers, demonstrating their significance in advancing the understanding of fractional dynamics

Monch’s fixed point theorem, a pivotal result in the field of functional analysis and nonlinear analysis, is a vital tool for addressing existence problems in differential equations, see [5,6,7]. This theorem, a refinement and extension of the classic Leray-Schauder principle, is particularly effective in dealing with compact operators in Banach spaces. Monch’s theorem asserts the existence of a fixed point for a continuous and compact operator under specific boundary conditions. This theorem has found profound applications in proving the existence of solutions for various types of differential equations, including fractional differential equations, which are often challenging to solve using traditional methods. The importance of Monch’s fixed point theorem lies in its ability to handle non-linearities and more complex system dynamics, making it a cornerstone in the mathematical analysis of numerous physical and engineering problems. Its applicability in such a wide array of scenarios underscores its significance in both theoretical mathematics and applied sciences.

Ulam-Hyers stability in differential equations is a concept that addresses the resilience of solutions in the face of small perturbations. This stability criterion, emerging from the works of Ulam and Hyers, focuses on the behavior of differential equations when subjected to minor alterations in initial conditions or parameters. In essence, it examines whether small changes in the input of an equation lead to only small deviations in the solution, ensuring the robustness and reliability of the system modeled by the equation, see [31,32,33]. This form of stability is particularly crucial in applied mathematics and physics, where precise solutions are often impractical, and approximate solutions must remain consistent and reliable under slight variations. Ulam-Hyers stability has become a key concept in the study of both ordinary and fractional differential equations, providing a framework to assess the practical feasibility of solutions in real-world scenarios, such as engineering and biological systems, where exact conditions can rarely be guaranteed, see [34,35,36].

In summary, the study of fractional differential equations is a vibrant and continually evolving field, with vast potential for theoretical exploration and practical application. The progress made in proving the existence of solutions for these systems lays a strong foundation for further research and development in this intriguing and valuable area of mathematics. The Caputo–Hadamard fractional derivative represents a significant advancement in the field of fractional calculus, blending the concepts of the Caputo derivative and the Hadamard derivative see [37, 38]. This derivative is particularly notable for its application in problems where standard differentiation does not suffice, especially in handling functions with singularities. The Caputo–Hadamard derivative is defined for functions on a semi-infinite interval, making it a valuable tool in analyzing systems with non-local and hereditary properties [39]. Its distinct formulation allows for the incorporation of both the non-locality inherent in fractional calculus and the specific characteristics of singular functions, providing a more comprehensive approach for modeling complex phenomena [40]. This derivative is increasingly relevant in various scientific and engineering fields, where it offers a refined mathematical framework for dealing with irregular and fractal-like structures, and it continues to be a subject of active research in the exploration of advanced differential equations.

In 2008, Benchohra et al. [41], discussed the Caputo fractional derivative of order p

$$\begin{aligned} ^c{D}^p\Phi (\tau )=\mathfrak {F}_{1}(\tau , \Phi (\tau )), \quad{} & {} for\quad a.e \quad \tau \in [0,\mathcal {T}], \quad \ 0<p\le 1, \\{} & {} a_1\Phi (0)+\zeta _{1}\Phi (\tau )=\varrho _1 \end{aligned}$$

with $\mathfrak {F}_{1}:[0,T]\times R \rightarrow R$ is a given continuous function and $a_1,\zeta _{1},\varrho _1 \in R$ such that $a_1+\zeta _{1}\ne 0$.

In 2017, Arioua et.al. [42] consider the following problem

$$\begin{aligned} ^cD_{1^+}^{p}\Phi (\tau )+\mathfrak {F}_{1}(\tau , \Phi (\tau ))=0, \quad for\quad 1<\tau<e, \quad \ 2<p\le 3, \end{aligned}$$

with the fractional boundary conditions:

$$\begin{aligned} \Phi (1)=\Phi ^{'}(1)=0, \quad (^cD_{1^+}^{p-1}\Phi )(e)= (^cD_{1^+}^{p-2}\Phi )(e)=0 \end{aligned}$$

where $^cD^{p}$ denotes the C-H FDEs of order p and $\mathfrak {F}_{1}:[1,e]\times R \rightarrow R$.

In 2018, Benhamida et.al. [43] investigated the following Caputo-Hadamard fractional differential equations with the boundary conditions:

$$\begin{aligned} ^c_HD^{p}\Phi (\tau ) = \mathfrak {F}_{1}(\tau , \Phi (\tau )), \quad{} & {} for\quad a.e \quad \tau \in [1,\mathcal {T}], \quad \ 0<p\le 1, \\ {}{} & {} a_1\Phi (1)+\zeta _{1}\Phi (\tau )=\varrho _1, \end{aligned}$$

where $^c_HD^{p}$ denotes the C-H FDEs of order p with $\mathfrak {F}_{1}:[1,\mathcal {T}]\times R \rightarrow R$ and the real constants $a_1,\zeta _{1}$ and $\varrho _1$ such that $a_1+\zeta _{1}\ne 0$.

Motivated by the above mentioned works, we consider the system of hybrid nonlinear Caputo–Hadamard (C-H) fractional differential equations:

$$\begin{aligned} \left. \begin{array}{cl} _H^cD^{\xi _{1}}\left[ z(\tau )\right] =\Upsilon _1(\tau ,z(\tau ),\Phi (\tau )), \ \tau \in [1,\mathcal {T}], \ 0<\xi _{1}\le 1,\\ _H^cD^{\varpi _1}\left[ \Phi (\tau )\right] =\Upsilon _2(\tau ,z(\tau ),\Phi (\tau )), \ \tau \in [1,\mathcal {T}], \ 0<\varpi _1\le 1, \end{array} \right. \end{aligned}$$

(1)

supplemented with

$$\begin{aligned} \left. \begin{array}{cl} &{} a_1z(1)+\zeta _{1}z(\tau )=\varrho _1, \\ &{} a_2\Phi (1)+\zeta _{2}\Phi (\tau )=\varrho _{2} \end{array} \right. \end{aligned}$$

(2)

where $_H^cD^{\xi _{1}}$, $_H^cD^{\varpi _1}$ denote the Caputo-Hadamard (C-H) fractional derivatives of orders $\xi _{1}$ and $\varpi _1$ respectively, The given continuous functions $\Upsilon _i:[1,\mathcal {T}]\times R \times R \rightarrow R ,$ i=1,2 with $a_i,b_i$ and $c_i \in R$, i=1,2.

Now, we extended the problem considered in [43] to a boundary value problem of coupled hybrid Caputo–Hadamard (C-H) fractional differential equations. For the existence part of the solution we use Schaefer’s fixed point theorem and the uniqueness, we apply Banach contraction mapping principle.

Remark

[41] Problems defined on 1 and 2 are applied for an initial value problem when ($a_i$=1 and $b_i$=0), boundary value problem when ($a_i$=0 and $b_i$=1) and has antiperiodic solutions ( $a_i$=1 and $b_i$=1, $c_i=0$), i=1,2.

Sect. 2 introduces the main concepts, lemmas, and definitions. In additionto, the discussion of the auxiliary lemma where we introduce the solution of our proposed system, Sect. 3 studies the existence of the solution, Sect. 4 investigates the stability, and Sect. 5 discuss an applicable example of our results. Finally conclusion alongside with future work is mentioned in Sect. 6.

2 Preliminaries

Definition 2.1

[44] If $h_1$: $[1,+\infty )$ $\rightarrow R$, a continuous function then the Hadamard fractional integral (HFI) of order ${q_1}$ is defind by

$$\begin{aligned} _HI^{q_1} h_1(\tau )=\frac{1}{\Gamma ({q_1})}\int _{1}^{\tau } \Big (log\frac{\tau }{s}\Big )^{{q_1}-1}\frac{h_1(s)}{s}ds, \quad {q_1}>0,\quad \tau >1 ~ \end{aligned}$$

provided the integral exists.

Definition 2.2

[44] For the function $h_1$: [1,$+\infty$] $\rightarrow$ $R$, the Hadamard fractional derivative of order $\xi _{1}$ is defined as

$$\begin{aligned} (_HD^{q_1} h_1)(\tau )= & {} \frac{1}{\Gamma (n-{q_1})}\Big (\frac{d}{dt}\Big )^{n}\int _{1}^{\tau } \Big (ln\frac{\tau }{s}\Big )^{n-q_1-1}\frac{h_1(s)}{s}ds, \quad n-1<{q_1}<n, \\ {}= & {} \delta ^n(_HI^{n-q_1}h_1)(\tau ) \end{aligned}$$

where $n=[q_1]+1, \ [{q_1}]$ is the integer part of the real number.

Definition 2.3

[45] The C-H fractional derivative of order $q_1$ where $q_1\ge 0$, $n-1< q_1 <n,$ with n=$[ q_1]+1$ and $h_1 \in AC_\delta ^n$[1,$\infty$)

$$\begin{aligned} (_H^cD^{q_1}h_1)(\tau )&=\frac{1}{\Gamma (n-q_1)}\int _{1}^{\tau }(log\frac{\tau }{s})^{n-q_1-1}\delta ^{n}h_1(s)\frac{ds}{s}\\&=_HI^{n-q_1}(\delta ^nh_1)(\tau ). \end{aligned}$$

Lemma 2.4

Let $h_1 \in AC_\delta ^n[1,+\infty ) \quad and \quad q_1>0$ then

$$\begin{aligned} _HI^{q_1} (_H^cD^{q_1} h_1)(\tau )=h_1(\tau )-\sum _{i=0}^{n-1}\dfrac{\delta ^ih_1(1)}{i!}(log\tau )^i. \end{aligned}$$

Definition 2.5

The Kuratowski measure of noncompactness $k(\cdot )$. Defines on bounded set $\mathcal {U}$ of Banach space $\mathcal {Q}$ is:

$$\begin{aligned} k(\mathcal {U}):= \inf \{r>0:\mathcal {U} = \cup _{i=1}^{m} \ \text{ and } \text{ diam }(\mathcal {U}_{i}) \le r \ \text{ for } \ 1\le i\le m\}. \end{aligned}$$

Lemma 2.6

Given the Banach space $\mathcal {Q}$ with $\mathcal {U,V}$ are two bounded proper subsets of $\mathcal {Q}$, then the following properties hold true

• If $\mathcal {U}\subset \mathcal {V}$, then $k(\mathcal {U}) \le k(\mathcal {V})$;

• k$(\mathcal {U}) = k(\bar{\mathcal {U}})=k(\overline{conv} \ \mathcal {U})$;

• $\mathcal {U}$ is relatively compact k($\mathcal {U}$)=0;

• k ($\delta \mathcal {U}$)= $|\delta |k(\mathcal {U}), \ \delta \in \mathbb {R};$

• k $(\mathcal {U}\cup \mathcal {V}) = \max \{k(\mathcal {U}),k(\mathcal {V})\}$;

• $(\mathcal {U}+\mathcal {V}) \le k(\mathcal {U}) +k (\mathcal {V}), \ \mathcal {U}+\mathcal {V} = \{x|x = u +v, \ u \in \mathcal {U}, v \in \mathcal {V}\}$;

• k$(\mathcal {U}+y)=k(\mathcal {U}), \ \forall \ y \in \mathcal {Q}$.

Definition 2.7

Given the function $\psi : [a,\mathcal {T}] \times \mathcal {Q} \rightarrow \mathcal {Q}, \psi$ satisfy the Caratheodory conditions, if the following conditions applies:

• $\psi$ is measurable in $\omega$ for $z \in \mathcal {Q}$.

• $\psi$ is continuous in $z \in \mathcal {Q}$ for $\omega \in [a,\mathcal {T}]$.

Theorem 2.8

(Monch’s fixed point theorem) Given a bounded, closed, and convex subset $\Omega \subset \mathcal {Q}$, such that $0 \in \Omega$, let also $\mathcal {T}$ be a continuous mapping of $\Omega$ into itself.

If $\mathcal {S} = \overline{conv} \mathcal {T} (\mathcal {S})$, or $\mathcal {S} = \mathcal {T} (\mathcal {S}) \cap \{0\}$, then $k(\mathcal {S})=0$, satisfied $\forall \mathcal {S} \subset \Omega$, then $\mathcal {T}$ has a fixed point.

Lemma 2.9

Suppose $h_1:[1,+\infty )\rightarrow R$ is a continuous function and a solution z is defined by

$$\begin{aligned} z(\tau )&=\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau } (log\dfrac{\tau }{s})^{\xi _{1}-1}h_1(s)\dfrac{d}{ds}-\dfrac{\zeta _{1}}{\Gamma (\xi _{1}) (a_1+\zeta _{1})}\nonumber \\ {}&\quad \int _{1}^{\tau }(log\dfrac{T}{s})^{\xi _{1}-1}h_1(s)\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}} \end{aligned}$$

(3)

if and only if

$$\begin{aligned}&_H^cD^{\xi _{1}}z(\tau )=h_1(\tau ), \quad \quad 0<\xi _{1}<1 \end{aligned}$$

(4)

$$\begin{aligned}&\quad and \ \ a_1z(1)+\zeta _{1}z(\tau )=\varrho _1 \end{aligned}$$

(5)

Proof

Assume z satisfies (4) then Lemma 2.4 implies

$$\begin{aligned} z(\tau )=_HI^{\xi _{1}}h_1(\tau )+d_1 \end{aligned}$$

(6)

when we apply the boundary condition (5), we get

$$\begin{aligned}&z(1)=d_1&\\&z(\tau )=_HI^{\xi _{1}}h_1(\tau )+d_1&\\&a_1z(1)+\zeta _{1}z(\tau )=\varrho _1&\\&a_1d_1+\zeta _{1}[_HI^{\xi _{1}}h_1(\tau )+z(1)]=\varrho _1&\\&a_1z(1)+\zeta _{1}{}_HI^{\xi _{1}}h_1(\tau )+\zeta _{1}z(1)=\varrho _1&\\&(a_1+\zeta _{1})z(1)+\zeta _{1}{}_HI^{\xi _{1}}h_1(\tau )=\varrho _1&\\&z(1)=\dfrac{\varrho _1-\zeta _{1}{}_HI^{\xi _{1}}h_1(\tau )}{(a_1+\zeta _{1})}&\end{aligned}$$

which leads to the solution (3) that

$$\begin{aligned} z(\tau )=_HI^{\xi _{1}}h_1(\tau )-\dfrac{\zeta _{1}}{(a_1+\zeta _{1})}\quad _HI^{\xi _{1}}h_1(\tau )+\dfrac{\varrho _1}{a_1+\zeta _{1}} \end{aligned}$$

Conversely, Eqs. (4) –(5) hold for z. $\square$

3 Main results

Let us now consider a Banach space $\mathfrak {W}=\{\tilde{z}(\tau )/\tilde{z}(\tau )\in C ([1,\mathcal {T}])\}$ from $[1,\mathcal {T}]$ $\times R \rightarrow R$ endowed with the norm $\Vert \tilde{z}\Vert _{\infty }=sup\{|\tilde{z}(\tau )|:1\le \tau \le T\}$. Let the absolutely continuous function is defined as $AC_{\delta }^m([e_1,e_2]\times R , R )=\{h_1:[e_1,e_2]\times R \rightarrow R :\delta ^{n-1}h_1(\tau )\in AC([e_1,e_2]\times R , R )\}$, where $\delta =\tau \frac{d}{d\tau }$. Then the product space $(\mathfrak {W}\times \mathfrak {W}, \Vert (\tilde{z},\tilde{\Phi })\Vert )$ endowed with the norm $\left\| (\tilde{z},\tilde{\Phi })\right\| =\left\| \tilde{z}\right\| +\left\| \tilde{\Phi }\right\|$, $(\tilde{z},\tilde{\Phi })\in \mathfrak {W}\times \mathfrak {W}$, with the following assumptions,

• (A1) Assume the functions $\Upsilon _1,\Upsilon _2:[1,\mathcal {T}]\times R \times R \rightarrow R$ satisfy Caratheodory conditions,

• (A2) $l_{\Upsilon _1}, l_{\Upsilon _2} \in \mathcal {L}^{\infty }([1,\mathcal {T}],\mathbb {R}_{+})$, and there exist a nondecreasing conditions function $\varOmega _{\Upsilon _1},\varOmega _{\Upsilon _2}: \mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$, such that, $\forall \tau \in [1,\mathcal {T}], \forall (\Upsilon _1, \Upsilon _2) \in \mathfrak {M}$, we have

  $$\begin{aligned} ||\Upsilon _1(\tau , z, \Phi ) ||_{\infty } \le l_{\Upsilon _1} (\tau ) \varOmega _{\Upsilon _1} (||z||_{\infty } +||\Phi ||_{\infty }) \\ ||\Upsilon _2(\tau , z, \Phi ) ||_{\infty } \le l_{\Upsilon _2} (\tau ) \varOmega _{\Upsilon _2 } (||z||_{\infty } +||\Phi ||_{\infty }) \end{aligned}$$

• (A3) Let $\mathfrak {S} \subset \mathfrak {M} \times \mathfrak {M}$, be a bounded set, and $\forall \tau \in [1,\mathcal {T}]$, then

  $$\begin{aligned} \kappa (\Upsilon _1(\tau , \mathfrak {S})) \le l_{\Upsilon _1}(\tau )\kappa (\mathfrak {S}),\\ \kappa (\Upsilon _2(\tau , \mathfrak {S})) \le l_{\Upsilon _2}(\tau )\kappa (\mathfrak {S}). \end{aligned}$$

  For the ease of computational calculation, we pose

  $$\begin{aligned}&P_1=\Big [1+\dfrac{|\zeta _{1}|}{|a_1+\zeta _{1}|}\Big ]\dfrac{(logT)^{\xi _{1}}}{\Gamma (\xi _{1}+1)} , \end{aligned}$$

  (7)
  $$\begin{aligned}&P_2=\Big [1+\dfrac{|\zeta _{2}|}{|a_2+\zeta _{2}|}\Big ]\dfrac{(logT)^{\varpi _1}}{\Gamma (\varpi _1+1)};\nonumber \\ \ {}&Q_1= \dfrac{|\varrho _1|}{|a_1+\zeta _{1}|}<1 \quad and \quad \quad Q_2= \dfrac{|\varrho _{2}|}{|a_2+\zeta _{2}|}<1 \end{aligned}$$

  (8)

In view of Lemma 2.5, we define an operator $\varphi : \mathfrak {W}\times \mathfrak {W}\rightarrow \mathfrak {W}\times \mathfrak {W}$ and (1)-(2) becomes,

$$\begin{aligned} \varphi (z,\Phi )(\tau )&= \left( \begin{array}{cl} \mathcal {\varphi }_1(z,\Phi )(\tau ) \\ \mathcal {\varphi }_2(z,\Phi )(\tau ) \end{array} \right) , \end{aligned}$$

(9)

where

$$\begin{aligned} \varphi _1(z,\Phi )(\tau )&=\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1} \Upsilon _1(s)\dfrac{d}{ds}-\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\\&\quad \int _{1}^{\tau } \Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}\Upsilon _1(s)\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}} \end{aligned}$$

and

$$\begin{aligned} \varphi _2(z,\Phi )(\tau )&=\dfrac{1}{\Gamma {(\varpi _1)}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1}\Upsilon _2(s) \dfrac{d}{ds}-\dfrac{\zeta _{2}}{\Gamma (\varpi _1)(a_2+\zeta _{2})}\\&\quad \int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\varpi _1-1} \Upsilon _2(s)\dfrac{d}{ds}+\dfrac{\varrho _{2}}{a_2+\zeta _{2}} \end{aligned}$$

Theorem 3.1

Assume that the conditions (A1), (A2), and (A3) are satisfied. If $\max \{P_{1}\bar{l_{\Upsilon _1}},P_{2}\bar{l_{\Upsilon _2}}\} <1$, then there exist at least one solution for the boundary value problem Eq. (1) on $[1,\mathcal {T}]$.

Proof

Beginning with introduction the following continuous operator $\varphi : \mathscr {M} \rightarrow \mathscr {M}$, as

$$\begin{aligned} \varphi (z,\Phi )(\tau )&= \left( \begin{array}{cl} \mathcal {\varphi }_1(z,\Phi )(\tau ) \\ \mathcal {\varphi }_2(z,\Phi )(\tau ) \end{array} \right) , \end{aligned}$$

(10)

where

$$\begin{aligned} \varphi _1(z,\Phi )(\tau )&=\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}||\Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds} \\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}|| \Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\\ {}&\quad +\dfrac{\varrho _1}{a_1+\zeta _{1}} \end{aligned}$$

and

$$\begin{aligned} \varphi _2(z,\Phi )(\tau )&=\dfrac{1}{\Gamma {(\varpi _1)}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1}|| \Upsilon _2(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\\ {}&\quad -\dfrac{\zeta _{2}}{\Gamma (\varpi _1)(a_2+\zeta _{2})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\varpi _1-1}||\Upsilon _2(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\\ {}&\quad +\dfrac{\varrho _{2}}{a_2+\zeta _{2}} \end{aligned}$$

According to the conditions (A1) and (A2), the operator $\varphi$ is well defined. Then the following operator equation can be equivalent equation to the fractional equation given by Eq.(3).

$$\begin{aligned} (z,\Phi ) = \varphi (z,\Phi ). \end{aligned}$$

(11)

Subsequently, proving the existence of the solution to the Eq.(11) is equivalent to proving the existence of a solution to the Eq.(1).

Let $\Phi _{\epsilon } = \{(z,\Phi ) \in \mathfrak {M}: ||(z,\Phi )|| \le \epsilon , \epsilon > 0\},$ be a closed bounded convex ball in $\mathfrak {M}$ with

$$\begin{aligned} \epsilon \ge \bar{l_{\Upsilon _1}}P_1 \varOmega _{\Upsilon _1} (\epsilon ) + \bar{l_{\Upsilon _2}}P_2 \varOmega _{\Upsilon _2} (\epsilon ) + ||z|| + || \Phi ||, \end{aligned}$$

where $\bar{l_{\Upsilon _1}}= \displaystyle \sup _{1\le \tau \le \mathcal {T}}{l_{\Upsilon _1}}(\tau ),$

For the possibility of applying Mönch’s fixed point theorem, we will proceed in the proof in the form of four steps, and thus, we achieve the desired goal by proving the existence of a solution to the equation given in Eq. (1).

Firstly, we show that $\varphi \Phi _{\epsilon } \subset \Phi _{\epsilon }$ for this, we let $\tau \in [1,\mathcal {T}]$, and for any $(z,\Phi ) \in \Phi _{\epsilon }$ we have

$$\begin{aligned} ||\varphi _1(z,\Phi )||_{\infty }&=\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}|| \Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau } \Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}||\Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\\ {}&\quad +\dfrac{\varrho _1}{a_1+\zeta _{1}}, \end{aligned}$$

Based on (A2), $\forall \ \tau \in [1,\mathcal {T}]$, observe that

$$\begin{aligned} ||\Upsilon _1(\tau ,z(\tau ),\Phi (\tau ))||_{\infty }&\le \bar{l_{\Upsilon _1}}(\tau ) \varOmega _{\Upsilon _1} (||z(\tau )||_{\infty }+||\Phi (\tau )||_{\infty }) \\ {}&\le \bar{l_{\Upsilon _1}}\varOmega _{\Upsilon _1} (\epsilon ), \end{aligned}$$

then

$$\begin{aligned} ||\varphi _1(z,\Phi )||_{\infty }&=\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}\bar{l_{\Upsilon _1}}(\tau ) \varOmega _{\Upsilon _1} (||z(\tau )||_{\infty }+||\Phi (\tau )||_{\infty })\dfrac{d}{ds}\nonumber \\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau } \Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}\bar{l_{\Upsilon _1}}(\tau ) \varOmega _{\Upsilon _1} (||z(\tau )||_{\infty }\nonumber \\&\quad +||\Phi (\tau )||_{\infty })\dfrac{d}{ds} +\dfrac{\varrho _1}{a_1+\zeta _{1}},\nonumber \\&\le \bar{l_{\Upsilon _1}}(\tau ) \varOmega _{\Upsilon _1} (||z(\tau )||_{\infty }+||\Phi (\tau )||_{\infty })\Biggl \{\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau } \Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}\dfrac{d}{ds} \nonumber \\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau } \Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}}\Biggr \},\nonumber \\&\le \bar{l_{\Upsilon _1}}P_1 \varOmega _{\Upsilon _1} (\epsilon ). \end{aligned}$$

(12)

Similarly

$$\begin{aligned}&||\varphi _2(z,\Phi )||_{\infty } =\dfrac{1}{\Gamma {(\varpi _1)}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1} \bar{l_{\Upsilon _2}}(\tau ) \varOmega _{\Upsilon _2} (||z(\tau )||_{\infty }+||\Phi (\tau )||_{\infty })\dfrac{d}{ds} \\&-\dfrac{\zeta _{2}}{\Gamma (\varpi _1)(a_2+\zeta _{2})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\varpi _1-1} \bar{l_{\Upsilon _2}}(\tau ) \varOmega _{\Upsilon _2} (||z(\tau )||_{\infty }+||\Phi (\tau )||_{\infty })\dfrac{d}{ds} \\ {}&\quad +\dfrac{\varrho _{2}}{a_2+\zeta _{2}},\\&\quad \le \bar{l_{\Upsilon _2}}(\tau ) \varOmega _{\Upsilon _2} (||z(\tau )||_{\infty } +||\Phi (\tau )||_{\infty })\Biggl \{\dfrac{1}{\Gamma {(\varpi _1)}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1} \dfrac{d}{ds} \\&-\dfrac{\zeta _{2}}{\Gamma (\varpi _1)(a_2+\zeta _{2})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\varpi _1-1} \dfrac{d}{ds}+\dfrac{\varrho _{2}}{a_2+\zeta _{2}}\Biggr \}, \end{aligned}$$

$$\begin{aligned} \le&\bar{l_{\Upsilon _2}}P_2 \varOmega _{\Upsilon _2} (\epsilon ). \end{aligned}$$

(13)

Eq.(12) and Eq. (13) implies that

$$\begin{aligned} ||(z,\Phi )||_{\infty }&= ||\varphi _1(z,\Phi )||_{\infty } + ||\varphi _2(z,\Phi )||_{\infty } \\ {}&\le \bar{l_{\Upsilon _1}}P_1 \varOmega _{\Upsilon _1} (\epsilon ) + \bar{l_{\Upsilon _2}}P_2 \varOmega _{\Upsilon _2} (\epsilon ) \\ {}&\le \epsilon . \end{aligned}$$

This proves that $\varphi \Phi _{\epsilon } \subset \Phi _{\epsilon }$.

Secondly, we need to show the continuity for $\varphi$ to see this, we take the sequence $\{u_{n} = (z_{n},\Phi _{n})\} \in \Phi _{\epsilon }$, such that $u_{n} \rightarrow u = (z,\Phi )$ as $n \rightarrow \infty$.

Owing to the Carathéodory continuity of $\varsigma$, it is obvious that

$$\begin{aligned} \varsigma ((\cdot ),z_{n}(\cdot ),\Phi _{n}(\cdot )) \rightarrow \varsigma ((\cdot ),z(\cdot ),\Phi (\cdot )) \end{aligned}$$

as $n \rightarrow \infty$. Keeping in mind was given in (A2), one can deduce that

$$\begin{aligned} \Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1} || \varsigma ((\cdot ),z_{n}(\cdot ),\Phi _{n}(\cdot )) - \varsigma ((\cdot ),z(\cdot ),\Phi (\cdot )) || \le \bar{l_{\Upsilon _1}} \varOmega _{\Upsilon _1} (\epsilon ) \Biggl \{ \Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1}\Biggr \}. \end{aligned}$$

Together with the Lebesgue dominated convergence theorem and the fact that the function

$$\begin{aligned} r \rightarrowtail \bar{l_{\Upsilon _1}} \varOmega _{\Upsilon _1} (\epsilon ) \Biggl \{ \Big (log\dfrac{\tau }{s}\Big )^{\varpi _1-1}\Biggr \} \end{aligned}$$

is the Lebsegue integrable on $[1,\mathcal {T}]$, we have

$$\begin{aligned}&\Big (\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}|| \varsigma ((\cdot ),z_{n}(\cdot ),\Phi _{n}(\cdot )) - \varsigma ((\cdot ),z(\cdot ),\Phi (\cdot )) ||\dfrac{d}{ds} \\&-\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}|| \varsigma ((\cdot ),z_{n}(\cdot ),\Phi _{n}(\cdot )) \\&\quad - \varsigma ((\cdot ),z(\cdot ),\Phi (\cdot )) || \dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}}\Big )\rightarrow 0 \end{aligned}$$

as $n \rightarrow \infty$.

Yields to $|| \varphi _1(z_{n},\Phi _{n})(\tau )- \varphi _1(z,\Phi )(\tau ) ||_{\infty } \rightarrow 0$ as $n \rightarrow \infty$.

$\forall \tau \in [1,\mathcal {T}],$ we get

$$\begin{aligned} || \varphi _{1}(z_{n},\Phi _{n})- \varphi _{1}(z,\Phi )||_{\infty } \rightarrow 0 \ \text{ as } \ n \rightarrow \infty , \end{aligned}$$

(14)

that is the operator $\varphi _{1}$ is continuous.

In a like manner, we have

$$\begin{aligned} || \varphi _{1}(z_{n},\Phi _{n})- \varphi _{1}(z,\Phi )||_{\infty } \rightarrow 0 \ \text{ as } \ n \rightarrow \infty , \end{aligned}$$

(15)

Combining (14) and (15), we obtain

$$\begin{aligned} || \varphi (z_{n},\Phi _{n})- \varphi (z,\Phi )||_{\infty } \rightarrow 0\ \text{ as } \ n \rightarrow \infty , \end{aligned}$$

(16)

From Eq. (16), we conclude that the operator is continuous.

Third, to verify the equicontinuity for the operator $\varphi$, let $\tau _{1}, t_{2} \in [1,\mathcal {T}], (\tau _{1}, \tau _{2})$ and for any then $(z,\Phi ) \in \Phi _{\epsilon }$, then

$$\begin{aligned}&|| \varphi _{1}(z,\Phi )(\tau _{2}) - \varphi _{1}(z,\Phi )(\tau _{1})||_{\infty } \nonumber \\&\quad \le \frac{1}{\Gamma (\xi _{1})}\int _{1}^{\tau _{1}}\Bigg [(log\dfrac{\tau _{2}}{s})^{\xi _{1}-1}-(log\dfrac{\tau _{1}}{s})^{\xi _{1}-1}\Bigg ] \left| \Upsilon _1(s,z(s),\Phi (s))\right| \dfrac{d}{ds}\nonumber \\&\quad \quad +\frac{1}{\Gamma (\xi _{1})}\int _{\tau _{1}}^{\tau _{2}}(log\dfrac{\tau _{2}}{s})^{\xi _{1}-1} \left| \Upsilon _1(s,z(s),\Phi (s))\right| \dfrac{d}{ds} \nonumber \\&\quad \le (\bar{l_{\Upsilon _1}}(\tau ) \varOmega _{\Upsilon _1}(\epsilon )) \nonumber \\ {}&\quad \quad \times \Big [\frac{1}{\Gamma (\xi _{1})}\int _{1}^{\tau _{1}}\Bigg [(log\dfrac{\tau _{2}}{s})^{\xi _{1}-1} -(log\dfrac{\tau _{1}}{s})^{\xi _{1}-1}\Bigg ] \left| \Upsilon _1(s,z(s),\Phi (s))\right| \dfrac{d}{ds} \nonumber \\&\quad \quad +\frac{1}{\Gamma (\xi _{1})}\int _{\tau _{1}}^{\tau _{2}}(log\dfrac{\tau _{2}}{s})^{\xi _{1}-1} \left| \Upsilon _1(s,z(s),\Phi (s))\right| \dfrac{d}{ds} \Big ] \rightarrow 0 \ \text{ as } \ \tau _{1} \rightarrow \tau _{2}. \end{aligned}$$

(17)

Similarly, we get

$$\begin{aligned}&|| \varphi _{2}(z,\Phi )(\tau _{2}) - \varphi _{2}(z,\Phi )(\tau _{1})||_{\infty } \nonumber \\&\quad \le \frac{1}{\Gamma (\varpi _1)}\int _{1}^{\tau _{1}}\Bigg [(log\dfrac{\tau _{2}}{s})^{\varpi _1-1} -(log\dfrac{\tau _{1}}{s})^{\varpi _1-1}\Bigg ] \left| \Upsilon _2(s,z(s),\Phi (s))\right| \dfrac{d}{ds}\nonumber \\&\quad \quad +\frac{1}{\Gamma (\varpi _1)}\int _{\tau _{1}}^{\tau _{2}}(log\dfrac{\tau _{2}}{s})^{\varpi _1-1} \left| \Upsilon _2(s,z(s),\Phi (s))\right| \dfrac{d}{ds} \nonumber \\&\quad \le (\bar{l_{\Upsilon _2}}(\tau ) \varOmega _{\Upsilon _2}(\epsilon )) \nonumber \\ {}&\quad \quad \times \Big [\frac{1}{\Gamma (\varpi _1)}\int _{1}^{\tau _{1}}\Bigg [(log\dfrac{\tau _{2}}{s})^{\varpi _1-1} -(log\dfrac{\tau _{1}}{s})^{\varpi _1-1}\Bigg ] \left| \Upsilon _2(s,z(s),\Phi (s))\right| \dfrac{d}{ds} \nonumber \\&\quad \quad +\frac{1}{\Gamma (\varpi _1)}\int _{\tau _{1}}^{\tau _{2}}(log\dfrac{\tau _{2}}{s})^{\varpi _1-1} \left| \Upsilon _2(s,z(s),\Phi (s))\right| \dfrac{d}{ds} \Big ] \rightarrow 0 \ \text{ as } \ \tau _{1} \rightarrow \tau _{2}. \end{aligned}$$

(18)

Note that the R.H.S’s of the above inequalities of Eqs. (17) and (18) are free of $(z,\Phi ) \in \Phi _{\epsilon }$, which implies that $\varphi$ is equicontinuous and bounded.

Fourth and finally, we need to satisfy Mönch’s hypothesis, so we let $\mathfrak {U} = \mathfrak {U}_{1} \cap \mathfrak {U}_{2}$, where, $\mathfrak {U}_{2}, \mathfrak {U}_{1} \subseteq \Phi _{\epsilon }.$ Moreover, $\mathfrak {U}_1 \mathfrak {U}_{2}$ are assumed to be bounded and equicontinuous, such that

$$\begin{aligned} \mathfrak {U}_{1} \subset \overline{conv}(\varphi _{1}(\mathfrak {U}_{1})\cup \{0\}), \ \text{ and } \ \mathfrak {U}_{2} \subset \overline{conv}(\varphi _{2}(\mathfrak {U}_{2})\cup \{0\}), \end{aligned}$$

thus the functions $\mathscr {J}_{1}(\tau ) = \kappa (\mathfrak {U}_{1}(\tau )), \ \mathscr {J}_{2}(\tau ) = \kappa (\mathfrak {U}_{2}(\tau ))$ are continuous on $[1,\mathcal {T}]$. Based on lemma and (A3) we get

$$\begin{aligned}&\mathscr {J}_{1}(\tau ) = \kappa (\mathfrak {U}_{1}(\tau )) \le \kappa (\overline{conv}(\varphi _{1}(\mathfrak {U}_{1})\cup \{0\})) \le \kappa (\varphi _{1}(\mathfrak {U}_{1})(\tau )) \\&\quad \le \kappa \Bigg (\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}|| \Upsilon _1(s,z(s),\Phi (s))||_{\infty }(s)\dfrac{d}{ds} \\&\quad \quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1}) (a_1+\zeta _{1})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}|| \Upsilon _1(s,z(s),\Phi (s))||_{\infty }(s)\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}} : (z,\Phi ) \in \mathfrak {U}_{1} \Bigg ) \\&\quad \le \Bigg (\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau } \Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}\kappa (\varphi _{1}(s,\mathfrak {U}_{1}(s)))(s)\dfrac{d}{ds} \\&\quad \quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1} \kappa (\varphi _{1}(s,\mathfrak {U}_{1}(s)))(s)\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}} : (z,\Phi ) \in \mathfrak {U}_{1} \Bigg ) \\&\quad \le \Bigg (\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau } \Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}l_{\Phi _1}(s) \kappa ((\mathfrak {U}_{1}(s)))(s)\dfrac{d}{ds} \\&\quad \quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau } \Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}l_{\Phi _1}(s)\kappa ((\mathfrak {U}_{1}(s)))(s)\dfrac{d}{ds} +\dfrac{\varrho _1}{a_1+\zeta _{1}} : (z,\Phi ) \in \mathfrak {U}_{1} \Bigg ) \\&\quad \le P_{1} \bar{l_{\Upsilon _1}}||\mathscr {J}_{1}||_{\infty }. \end{aligned}$$

That is $||\mathscr {J}_{1}|| \le P_{1} \bar{l_{\Upsilon _1}}||\mathscr {J}_{1}||_{\infty }$, but it is assumed that $\max \{P_{1} \bar{l_{\Upsilon _1}}, P_{2} \bar{l_{\Upsilon _2}}\}<1$, which implies that $||\mathscr {J}_{1}||_{\infty } =0$, i.e $\mathscr {J}_{1}(\tau )=0, \ \forall \ \tau \in [1,\mathcal {T}]$.

In a like manner, we have $\mathscr {J}_{2}(\tau ) =0,\ \forall \ \tau \in [1,\mathcal {T}]$. So $\kappa (\mathfrak {U}(\tau )) \le \kappa (\mathfrak {U}_{1}(\tau ))=0$ and $\kappa (\mathfrak {U}(\tau )) \le \kappa (\mathfrak {U}_{2}(\tau ))=0$, which implies that $\mathfrak {U}(\tau )$ is relatively compact in $\mathfrak {M}\times \mathfrak {M}$. Now, Arzela-Ascoli is applicable, which means that $\mathfrak {U}$ is relatively compact in $\Phi _{\epsilon }$, and therefore, using theorem (9), we deduce that the operator has a fixed point (z,$\Phi$) (solution of the problem Eq. (1) on $\Phi _{\epsilon }$. And that ends the proof. $\square$

4 Hyers-Ulam stability

This section is devoted to the investigation of Hyers-Ulam stability for our proposed system. Consider the following inequality:

$$\begin{aligned} \left. \begin{array}{cl} _H^cD^{\xi _{1}}\left[ z(\tau )\right] -\Upsilon _1(\tau ,z(\tau ),\Phi (\tau )) \le \varepsilon _{1}, \ \tau \in [1,\mathcal {T}], \ 0<\xi _{1}\le 1,\\ _H^cD^{\varpi _1}\left[ \Phi (\tau )\right] -\Upsilon _2(\tau ,z(\tau ),\Phi (\tau ))\le \varepsilon _{2}, \ \tau \in [1,\mathcal {T}], \ 0<\varpi _1\le 1, \end{array} \right. \end{aligned}$$

(19)

where $\varepsilon _{1}, \varepsilon _{2}$ are given two positive real numbers.

Definition 4.1

Problem (1) is Hyers-Ulam stable if there exist $P_{i} >0, i=1,2,3,4$ such that for given $\varepsilon _{1}, \varepsilon _{2}>0$ and for each $(z,\Phi ) \in \mathcal {C}([1,\mathcal {T}] \times \mathbb {R}^{2}, \mathbb {R})$ of inequality (19), there exists a solution $(z^{*},\Phi ^{*}) \in \mathcal {C}([1,\mathcal {T}] \times \mathbb {R}^{2}, \mathbb {R})$ of problem (1) with

$$\begin{aligned}&|z(\tau ) - z^{*}(\tau )| \le P_{1} \varepsilon _{1}, \ \tau \in [1,\mathcal {T}]\\ {}&|\Phi (\tau ) - \Phi ^{*}(\tau )| \le P_{2} \varepsilon _{2}, \ \tau \in [1,\mathcal {T}]. \end{aligned}$$

Remark 4.2

$(z, \Phi )$ is a solution of inequality (19) if there exist function $\mathcal {Q}_{i} \in \mathcal {C}([1,\mathcal {T}], \mathbb {R}), i=1,2$ which depend upon $z, \Phi$ respectively, such that

$$\begin{aligned} |\mathcal {Q}_{1}(\tau )| \le \varepsilon _{1}, \ |\mathcal {Q}_{2}(\tau )| \le \varepsilon _{2}, \end{aligned}$$

$$\begin{aligned} \left. \begin{array}{cl} _H^cD^{\xi _{1}}\left[ z(\tau )\right] =\Upsilon _1(\tau ,z(\tau ),\Phi (\tau )) + \mathcal {Q}_{1}(\tau ), \ \tau \in [1,\mathcal {T}], \ 0<\xi _{1}\le 1,\\ _H^cD^{\varpi _1}\left[ \Phi (\tau )\right] =\Upsilon _2(\tau ,z(\tau ),\Phi (\tau ))+ \mathcal {Q}_{2}(\tau ), \ \tau \in [1,\mathcal {T}], \ 0<\varpi _1\le 1, \end{array} \right. \end{aligned}$$

(20)

Remark 4.3

If $(z,\Phi )$ represent a solution of inequality (19), then $(z,\Phi )$ is a solution of following inequality

$$\begin{aligned}&|z(\tau ) - z^{*}(\tau )| \le P_{1} \varepsilon _{1} + P_{2} \varepsilon _{2}, \ \tau \in [1,\mathcal {T}]\\ {}&|\Phi (\tau ) - \Phi ^{*}(\tau )| \le P_{1} \varepsilon _{1} + P_{2} \varepsilon _{2}, \ \tau \in [1,\mathcal {T}]. \end{aligned}$$

As from Remark 4.2, we have

$$\begin{aligned} \left. \begin{array}{cl} _H^cD^{\xi _{1}}\left[ z(\tau )\right] =\Upsilon _1(\tau ,z(\tau ),\Phi (\tau )) + \mathcal {Q}_{1}(\tau ), \ \tau \in [1,\mathcal {T}], \ 0<\xi _{1}\le 1,\\ _H^cD^{\varpi _1}\left[ \Phi (\tau )\right] =\Upsilon _2(\tau ,z(\tau ),\Phi (\tau ))+ \mathcal {Q}_{2}(\tau ), \ \tau \in [1,\mathcal {T}], \ 0<\varpi _1\le 1, \end{array} \right. \end{aligned}$$

With the help of Definition 4.1 and Remark 4.2 we verified Remark 4.3, in the following lines

$$\begin{aligned} (z)(\tau )&=\Bigg |(z)^{*}(\tau )+\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}|| \Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\nonumber \\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}\nonumber \\&\qquad || \Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}}\Bigg |\nonumber \\ |(z)(\tau ) -(z)^{*}(\tau )|&\le \Bigg |\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau }\Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}|| \Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}\nonumber \\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau }\Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}\nonumber \\&\qquad || \Upsilon _1(s,z(s),\Phi (s))||(s)\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}}\Bigg |\nonumber \\&\le \Bigg |\dfrac{1}{\Gamma {(\xi _{1})}}\int _{1}^{\tau } \Big (log\dfrac{\tau }{s}\Big )^{\xi _{1}-1}|\mathcal {Q}_{1}(\tau )|\dfrac{d}{ds}\nonumber \\&\quad -\dfrac{\zeta _{1}}{\Gamma (\xi _{1})(a_1+\zeta _{1})}\int _{1}^{\tau } \Big (log\dfrac{T}{s}\Big )^{\xi _{1}-1}|\mathcal {Q}_{1}(\tau )|\dfrac{d}{ds}+\dfrac{\varrho _1}{a_1+\zeta _{1}}\Bigg |\nonumber \\&\le \varepsilon _{1} \Biggl \{\Big [1+\dfrac{|\zeta _{1}|}{|a_1+\zeta _{1}|}\Big ] \dfrac{(logT)^{\xi _{1}}}{\Gamma (\xi _{1}+1)}\Biggr \} = \varepsilon _{1}P_{1}.\nonumber \\ |z(\tau ) - z^{*}(\tau )|&\le \varepsilon _{1}P_{1}. \end{aligned}$$

(21)

By the same method we can obtain that

$$\begin{aligned} |\Phi (\tau ) - \Phi ^{*}(\tau )| \le P_{2} \varepsilon _{2}, \end{aligned}$$

(22)

where $P_{1}, P_{2}$ are given by (7)-(8). Hence remark is verified, with the help of (21) and (22). Thus the nonlinear coupled system of Caputo–Hadamard fractional differential equations is Hyers-Ulam stable and consequently, the system (1) is Hyers-Ulam stable.

5 Example

Example 5.1

IN this section, we provide an applied example that supports the theoretical results reached through this study.

Define, $z_{0}=\{z=(z_1,z_2,z_3,\cdots ,z_{n},\cdots ):\lim _{n\rightarrow \infty }z_{n}=0\}$, it is obvious that $Z_{0}$ is a Banach space with $||z||_{\infty } = \sup _{1 \ge 1}|z_{n}|$.

for this, we consider the following boundary value problem

$$\begin{aligned} \left. \begin{array}{cl} _H^cD^{\xi _{1}}\left[ z(\tau )\right] =\Upsilon _1(\tau ,z(\tau ),\Phi (\tau )), \ \tau \in [1,\mathcal {T}], \ 0<\xi _{1}\le 1,\\ _H^cD^{\varpi _1}\left[ \Phi (\tau )\right] =\Upsilon _2(\tau ,z(\tau ),\Phi (\tau )), \ \tau \in [1,\mathcal {T}], \ 0<\varpi _1\le 1, \end{array} \right. \end{aligned}$$

(23)

$$\begin{aligned}&z(1)+z(e)=0, \nonumber \\&\Phi (1)+\Phi (e) =0, \end{aligned}$$

(24)

Here $\xi _{1}=\varpi _1=\frac{1}{2}$, T=e,$a_1=\zeta _{1}=a_2=\zeta _{2}=1,\varrho _1=\varrho _{2}=0$,

Now, let us take the example

$$\begin{aligned} \Upsilon _1(\tau ,z(\tau ),\Phi (\tau ))&= \Biggl \{\frac{1}{In t + 10}\Big (\frac{1}{4}+In (1+|z_{n}| + |\Phi _{n}|)\Big )\Biggr \}, n\ge 1,\\ \Upsilon _2(\tau ,z(\tau ),\Phi (\tau ))&= \Biggl \{\frac{t}{ 10}\Big (\frac{1}{n^{4}}+\tan ^{-1} (1+|z_{n}| + |\Phi _{n}|)\Big )\Biggr \}, n\ge 1, \end{aligned}$$

$\forall \tau \in [1,3],$ with ${z_{n}}_{n\ge 1},{\Phi _{n}}_{n\ge 1} \in z_{0}$, assumption (A1) of theorem 2 is satisfied. Furthermore,

$$\begin{aligned} ||\Upsilon _1(\tau ,z(\tau ),\Phi (\tau ))||&= \left\| \Biggl \{\frac{1}{In t + 10}\Big (\frac{1}{4}+In (1+|z_{n}| + |\Phi _{n}|)\Big )\Biggr \}\right\| _{\infty }\\ {}&\le \frac{1}{In t + 10} (||z||+1) \\&= l_{\Upsilon _1}(\tau )\varOmega _{\Upsilon _1}(||z||), \end{aligned}$$

similarly,

$$\begin{aligned} ||\Upsilon _2(\tau ,z(\tau ),\Phi (\tau ))||_{\infty }&= \left\| \Biggl \{\frac{t}{ 10}\Big (\frac{1}{n^{4}}+\tan ^{-1} (1+|z_{n}| + |\Phi _{n}|)\Big )\Biggr \}\right\| _{\infty }\\ {}&\le \frac{t}{ 10} (||z||+1) \\&= l_{\Upsilon _2}(\tau )\varOmega _{\Upsilon _2}(||z||), \end{aligned}$$

That is (A2) of theorem 2 is satisfied as well.

Next, if we consider the bounded subset $\mathscr {S} \subset z_{0} \times z_{0}$, we obtain

$$\begin{aligned} \kappa (\Upsilon _1(\tau , \mathfrak {S}))&\le l_{\Upsilon _1}(\tau )\kappa (\mathfrak {S}),\\ \kappa (\Upsilon _2(\tau , \mathfrak {S}))&\le l_{\Upsilon _2}(\tau )\kappa (\mathfrak {S}). \end{aligned}$$

where in our case, we have $l_{\Upsilon _1} = \frac{t}{In t + 9}, l_{\Upsilon _2} = \frac{t}{10}$, the latter two inequalities show that the conclusion (A2) of theorem 2 is satisfied.

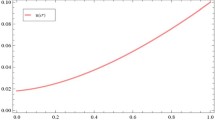
Finally, we calculate

$$\begin{aligned}&\bar{l_{\Upsilon _1}} = \frac{1}{10}, \le \Big [1+\dfrac{|\zeta _{1}|}{|a_1+\zeta _{1}|}\Big ]\dfrac{(logT)^{\xi _{1}}}{\Gamma (\xi _{1}+1)} , = 0.1693\\&\bar{l_{\Upsilon _2}} = \frac{3}{10}, \le \Big [1+\dfrac{|\zeta _{2}|}{|a_2+\zeta _{2}|}\Big ]\dfrac{(logT)^{\varpi _1}}{\Gamma (\varpi _1+1)}, = 0.5079. \end{aligned}$$

Then $\max \{P_{1}\bar{l_{\Upsilon _1}}, P_{2}\bar{l_{\Upsilon _2}}\} = \max \{0.1693, 0.5079\} = 0.5079 <1$. So all conditions of theorem 2 satisfied, that is the problem (1) has at least one solution.

6 Conclusion

In conclusion, the investigation into the existence of solutions for a system of fractional differential equations (FDEs) represents a significant advancement in the field of applied mathematics and its interdisciplinary applications. The rigorous approach adopted in this study, involving a blend of analytical and numerical methods, has not only confirmed the existence of solutions under specific conditions but has also highlighted the intricacy and richness of fractional calculus.

The utilization of various fixed point theorems and other mathematical tools has provided a solid foundation for proving the existence of solutions. These methodologies have proven to be effective in handling the non-linearity and complexity inherent in FDEs. Additionally, the exploration of Caputo and Riemann-Liouville fractional derivatives within these systems has further enriched our understanding of their dynamic properties.

Looking ahead, future work could focus on several promising areas. Firstly, extending the current models to more complex systems, including those with variable order or distributed order fractional derivatives, could provide deeper insights into the dynamics of more realistic models. Secondly, exploring the numerical solutions of these equations with advanced computational techniques would not only validate the theoretical findings but also pave the way for practical applications in engineering, physics, and other sciences.

Another intriguing avenue for future research is the application of these findings in real-world scenarios, such as in the fields of bioengineering, financial mathematics, and control systems, where fractional models often more accurately represent the underlying processes. Additionally, investigating the stability and control aspects of these systems could lead to the development of more robust and efficient methods for managing complex systems in various industries.