Skip to main content
SpringerLink
Log in

Entropy generation analysis on zero mass flux effects of nonlinear mixed convective Williamson nanofluid flow with christov-Cattaneo heat flux

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

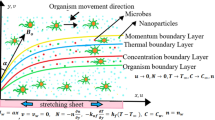
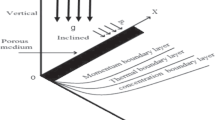
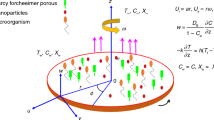
The passage of non-Newtonian fluids across the stretching plate exerts a significant impact and finds applications in various industrial sectors, such as fluidics networks, fluid agitation, thermal reactors, liquid chromatography, semiconductors, tissue regeneration, and gene delivery to organs. In this study, we investigated the hydrodynamic Williamson nanofluid flow over a stretchy surface with zero mass flux, Christov–Cattaneo (C–C) theory, non-linear mixed convection, and passive controls of nanomaterials. Thermophoresis and Brownian motion impressions are also taken in the present flow. The second law of thermodynamics is also used to determine the entropy generation. By using the proper similarity alterations, the PDEs (governing equations) are converted into non-linear ODEs. To crack the non-linear ODEs, the homotopy analysis method is used. There is a detailed discussion of the effects of magnetic, Weissenberg, radiation, Brownian motion, the Bejan parameter, and the entropy creation of various factors. Additionally, the heat, mass transfer rate, and skin friction are assessed. Also, compare skin friction and the Nusselt number with previous studies. The Weissenberg number and Brinkman parameter shows the opposite tendency in entropy generation and Bejan number profiles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data availability

Data available upon request.

Abbreviations

\(\hat{a}\) :

Stretchy rate \(\left( {{\text{s}}^{ - 1} } \right)\)

\(Bi\) :

Biot parameter

\(Be\) :

Bejan parameter

\(Br\) :

Brinkman parameter

\(B_{0}\) :

Constant magnetic field \(\left( {{\text{kgs}}^{ = 2 } {\text{A}}^{ - 1} } \right)\)

\(C\) :

Concentration \(\left( {{\text{kgm}}^{ - 3} } \right)\)

\(Cr\) :

Reaction rate number

\(c_{p}\) :

Specific heat at constant pressure \(\left( {{\text{J kg}}^{ - 1} {\text{K}}^{ - 1} } \right)\)

\(C_{\infty }\) :

Free stream concentration \(\left( {{\text{kgm}}^{ - 3} } \right)\)

\(C_{w}\) :

Fluid concentration at wall \(\left( {{\text{kgm}}^{ - 3} } \right)\)

\(C_{f}\) :

Skin-friction coefficient

\(D_{B} \;{\text{and}}\;D_{T}\) :

Brownian and Thermophoresis diffusion coefficients \(\left( {{\text{m}}^{2} {\text{s}}^{ - 1} } \right)\)

\(E_{G}\) :

Entropy creation number

\(Ec\) :

Eckert parameter

\(f\left( \eta \right)\) :

Velocity similarity function

\(f_{w}\) :

Suction/blowing parameter

\(h_{f}\) :

Convective heat transmission coefficient \(\left( {{\text{W}} {\text{m}}^{ - 1} {\text{K}}^{ - 1} } \right)\)

\(k\) :

Thermal conductivity \(\left( {{\text{W}} {\text{m}}^{ - 1} {\text{K}}^{ - 1} } \right)\)

\(Le\) :

Lewis number

\(M\) :

Hartmann parameter

\(Nb\) :

Brownian motion number

\(Nt\) :

Thermophoresis number

\(Nu\) :

Nusselt parameter

\(N^{*}\) :

Ratio of concentration to thermal buoyancy forces

\(Pr\) :

Prandtl number

\(Q_{0}\) :

Heat source/sink coefficient

\(\hat{q}\) :

Heat flux \(\left( {{\text{W}} {\text{m}}^{ - 2} } \right)\)

\(Rd\) :

Radiation number

\(Re\) :

Reynolds parameter

\(Sh\) :

Sherwood parameter

\(S\) :

Heat source parameter

\(T\) :

Temperature \(\left( {\text{K}} \right)\)

\(T_{\infty }\) :

Free stream temperature \(\left( {\text{K}} \right)\)

\(T_{f}\) :

Convective surface temperature \(\left( {\text{K}} \right)\)

\(\hat{u}_{{\text{w}}}\) :

Sheet velocity \(\left( {{\text{m}} {\text{s}}^{ - 1} } \right)\)

\(\hat{u}, \hat{v}\) :

Velocity apparatuses in \(\left( {\widehat{x, }\hat{y}} \right)\) axes \(\left( {{\text{m}} {\text{s}}^{ - 1} } \right)\)

\(\hat{v}_{{\text{w}}} > 0\) :

Suction velocity

\(\hat{v}_{{\text{w}}} < 0\) :

Blowing velocity

\(We\) :

Weissenberg number

\(\widehat{x, }\hat{y}\) :

Cartesian coordinates \(\left( {\text{m}} \right)\)

PDEs:

Partial differential equations

ODEs:

Ordinary differential systems

C–C:

Christov–Cattaneo heat flux

\(\beta\) :

Relaxation time

\(\beta_{t}\) :

Nonlinear mixed convection temperature component

\(\beta_{C}\) :

Nonlinear mixed convection concentration component

\(\phi \left( { \eta } \right)\;{\text{and}}\;\theta \left( { \eta } \right)\) :

Concentration and tedmperature similarity functions

\(\Gamma\) :

Non-dimensional velocity slip parameter

\(\gamma\) :

Non-dimensional thermal relaxation time

\(\eta\) :

Similarity parameter

\(\lambda_{T}\) :

Thermal relaxation time

\(\lambda\) :

Non-dimensional immovable

\({\upnu }\) :

Kinematic viscosity \(\left( {{\text{m}}^{2} {\text{s}}^{ - 1} } \right)\)

\(\Omega\) :

Non-dimensional temperature variance

\(\tau\) :

Ratio of the effective heat capacity

\(\rho\) :

Density \(\left( {{\text{kgm}}^{ - 1} } \right)\)

\(\sigma\) :

Electrical conductance variable \(\left(\mathrm{S m}\right)\)

\(\psi\) :

Stream function \(\left({\text{m}}{ {\text{s}}}^{-1}\right)\)

\(\zeta\) :

Non-dimensional concentration variance

References

  1. Choi, S.: Enhancing thermal conductivity of fluids with nanoparticles. ASME Int. Mech. Eng. Expo. 66, 99–105 (1995)

    Google Scholar 

  2. Kuznetsov, A., Nield, D.: Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 49, 243–247 (2010)

    Article  Google Scholar 

  3. Khan, W., Pop, I.: Boundary-layer flow of a nanofluid past a stretchy sheet. Int. J. Heat Mass Transfer. 53, 2477–2483 (2010)

    Article  Google Scholar 

  4. Haddad, Z., Abu-Nada, E., Oztop, H.F., et al.: Natural convection in nanofluids: are the thermophoresis and Brownian motion effects significant in nanofluid heat transfer enhancement. Int. J. Therm. Sci. 57, 152–162 (2012)

    Article  Google Scholar 

  5. Nadeem, S., Hussain, S.T., Lee, C.: Flow of Williamson fluid over a stretching sheet. Braz. J. Chem. Eng. 30, 619–625 (2013)

    Article  Google Scholar 

  6. Khan, S.U., Rauf, A., Shehzad, S.A., Abbas, Z., Javed, T.: Study of bioconvection flow in Oldroyd-B nanofluid with motile organisms and effective Prandtl approach. Physica A 527, 121179 (2019)

    Article  MathSciNet  Google Scholar 

  7. Bilal, S.M., Khan, N.Z., Nisar, R.: FEM simulations to analyze flow and thermal characteristics of Carreau non-Newtonian fluid in a square cavity. Int. J. Emerg. Multidiscipl. Math. (2023). https://doi.org/10.54938/ijemdm.2023.02.1.146

  8. Bilal, S., Pan, K., Ullah, A., Anwar, A., Akgül, A.: Aggregation of nanoparticles in flow of Carreau fluid containing gyrotactic microorganisms on extendable cylinder with viscous dissipation aspects by performing numerical simulations. Numer. Heat Transfer Part B Fundamentals (2023). https://doi.org/10.1080/10407790.2023.2287590

    Article  Google Scholar 

  9. Fourier, J.B.J.: Theorie Analytique De La Chaleur. Chez Firmin Didot, Paris (1822)

    Google Scholar 

  10. Cattaneo, C.: Sulla conduzionedelcalore. Atti del Seminario Matematico e Fisico dell Universita di Modena e Reggio Emilia. 3, 83–101 (1948)

    Google Scholar 

  11. Christov, C.I.: On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 36, 481–486 (2009)

    Article  MathSciNet  Google Scholar 

  12. Loganathan, K., Sivasankaran, S., Bhuvaneswari, M., Rajan, S.: Second-order slip, cross-diffusion and chemical reaction effects on magneto-convection of Oldroyd-B liquid using Cattaneo-Christov heat flux with convective heating. J. Thermal Anal. Calorim. 136, 401–409 (2019)

    Article  Google Scholar 

  13. Imtiaz, M., Alsaedi, A., Shaq, A., Hayat, T.: Impact of chemical reaction on third grade fluid flow with Cattaneo-Christov heat flux. J. Mol. Liq. 229, 501–507 (2017)

    Article  Google Scholar 

  14. Ramadevi, B., Kumar, K.A., Sugunamma, V., et al.: Magnetohydrodynamic mixed convective flow of micropolar fluid past a stretching surface using modified Fourier’s heat flux model. J. Therm. Anal. Calorim. (2019). https://doi.org/10.1007/s10973-019-08477-1

    Article  Google Scholar 

  15. Rashidi, M.M., Ali, M., Freidoonimehr, N., Nazari, F.: Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 55, 497–510 (2013)

    Article  Google Scholar 

  16. Khan, M.I., Alzahrani, F.: Transportation of heat through Cattaneo-Christov heat flux model in non-Newtonian fluid subject to internal resistance of particles. Appl. Math. Mech.-Engl. Ed. 41, 1157–1166 (2020)

    Article  MathSciNet  Google Scholar 

  17. López, A., Ibáñez, G., Pantoja, J., Moreira, J., Lastres, O.: Entropy generation analysis of MHD nanofluid flow in a porous vertical microchannel with nonlinear thermal radiation, slip flow and convective-radiative boundary conditions. Int. J. Heat Mass Transfer. 107, 982–994 (2017)

    Article  Google Scholar 

  18. Khan, M.I., Hayat, T., Waqas, M., Khan, M.I., Alsaedi, A.: Entropy generation minimization (EGM) in nonlinear mixed convective flow of nanomaterial with Joule heating and slip condition. J. Mol. Liq. 256, 108–120 (2018)

    Article  Google Scholar 

  19. Qing, J., Bhatti, M.M., Abbas, M.A., Rashidi, M.M., Ali, M.E.S.: Entropy generation on MHD Casson nanofluid flow over a porous stretchy/shrinking surface. Entropy 18, e18040123 (2016)

    Article  Google Scholar 

  20. Sheikholeslami, M., Ganji, D.: Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Physica A 417, 273–286 (2015)

    Article  Google Scholar 

  21. Liao, S., Tan, Y.A.: general approach to obtain series solutions of nonlinear differential. Stud. Appl. Math. 119(4), 297–354 (2007)

    Article  MathSciNet  Google Scholar 

  22. Loganathan, K., Rajan, S.: An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J. Therm. Anal. Calorim. 141, 2599–2612 (2020)

    Article  Google Scholar 

  23. Rashidi, M.M., Bagheri, S., Momoniat, E., Freidoonimeh, N.: Entropy analysis of convective MHD flow of third grade non-Newtonian fluid over a stretchy sheet. Ain Shams Eng. J. 8, 77–85 (2017)

    Article  Google Scholar 

  24. Eswaramoorthi, S., Sivasankaran, S., Bhuvaneswari, M., Rajan, S.: Soret and Dufour effects on viscoelastic boundary layer flow over a stretchy surface with convective boundary condition with radiation and chemical reaction. Sci Iran B. 23(6), 2575–2586 (2016)

    Google Scholar 

  25. Aquino, A.I., Ma, L., Bo-ot, T.: Multivalued behavior for a two-level system using Homotopy Analysis Method. Physica A 443, 358–371 (2016)

    Article  MathSciNet  Google Scholar 

  26. Chu, Y.M., Nazeer, M., Khan, M.I., Ali, W., Zafar, Z., Kadry, S., Abdelmalek, Z.: Entropy analysis in the Rabinowitsch fluid model through inclined Wavy Channel: constant and variable properties. Int. Commun. Heat Mass Transfer 119, 104980 (2020)

    Article  Google Scholar 

  27. Hayat, T., Shafiq, A., Alsaedi, A.: Effect of joule heating and thermal radiation in flow of third grade fluid over radiative surface. PLoS ONE 9(1), e83153 (2014)

    Article  Google Scholar 

  28. Ghasemi, S.E., Hatami, M., Sarokolaie, A.K., Ganji, D.: Study on blood flow containing nanoparticles through porous arteries in presence of magnetic field using analytical methods. Physica E 70, 14656 (2015)

    Article  Google Scholar 

  29. Wang, C.Y.: Free convection on a vertical stretching surface. ZAMM J. Appl. Math. Mech. 69, 418–420 (1989)

    Article  Google Scholar 

  30. Reddy Gorla, R., Sidawi, I.: Free convection on a vertical stretching surface with suction and blowing. Appl. Sci. Res. 52, 247–257 (1994)

    Article  Google Scholar 

  31. Khan, W.A., Pop, I.: Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53, 2477–2483 (2010)

    Article  Google Scholar 

  32. Makinde, O.D., Aziz, A.: Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50, 1326–1332 (2011)

    Article  Google Scholar 

  33. Gorla, R.S.R., Gireesha, B.J.: Dual solutions for stagnation-point flow convective heat transfer of a Williamson nanofluid past a stretching/shrinking sheet. Heat Mass Trans. 52, 1153–1162 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, SRM Institute of Science and Technology, SRM Nagar, Kattankulathur, Chengalpattu, 603203, Tamil Nadu, India

    D. Mahalakshmi & B. Vennila

  2. Department of Mathematics and Statistics, Manipal University Jaipur, Jaipur, 303007, Rajasthan, India

    K. Loganathan

Authors
  1. D. Mahalakshmi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. Vennila
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Loganathan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Vennila.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahalakshmi, D., Vennila, B. & Loganathan, K. Entropy generation analysis on zero mass flux effects of nonlinear mixed convective Williamson nanofluid flow with christov-Cattaneo heat flux. J. Appl. Math. Comput. 70, 1171–1192 (2024). https://doi.org/10.1007/s12190-024-02005-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-024-02005-7

Keywords

Search

Navigation