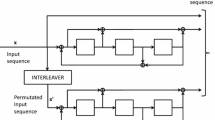
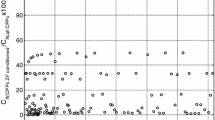
Abstract
In this paper, we propose a method for searching interleavers within a certain class, with the aim of designing turbo codes with good distance spectrum. The method is based on a modified version of Garello’s algorithm and consists in the calculation of frame error rate truncated upper bound. Here, it is applied to quadratic permutation polynomial (QPP) interleavers able to outperform those chosen for the long-term evolution (LTE) standard, for lengths up to 1,504 bits. Three classes of interleavers have been analyzed: (1) the set of QPP interleavers with the largest spread, (2) the set of QPP interleavers with a spread parameter equal to that of LTE interleaver and the highest refined nonlinearity degree, and (3) the complete set of all QPP interleavers for lengths up to 1,008. The distance spectrum optimization is made for all classes. Compared to previous methods for finding QPP-based interleavers, the search complexity is reduced, with improved performances in terms of search time, allowing interleavers of higher length. For lengths up to approximately 450, the best interleavers were found in the first class. For longer lengths, the second class contained the best ones.









Similar content being viewed by others
References
Garello R, Pierleoni P, Benedetto S (2001) Computing the free distance of turbo codes and serially concatenated codes with interleavers: algorithms and applications. IEEE J Sel Areas Commun 19(5):800–812
Trifina L, Tarniceriu D, Munteanu V. Improved QPP interleavers for LTE Standard, IEEE International Symposium on Signals, Circuits and Systems (ISSCS 2011), Iasi, Romania, pp. 403–406, June 30–July 1, 2011.
3GPP TS36.212, v8.3.0 (2008–05), Multiplexing and channel coding
Sun J, Takeshita OY (2005) Interleavers for turbo codes using permutation polynomial over integers rings. IEEE Trans Inf Theory 51(1):101–119
Takeshita OY (2006) On maximum contention-free interleavers and permutation polynomials over integers rings. IEEE Trans Inf Theory 52(3):1249–1253
Ryu J, Takeshita OY (2006) On quadratic inverses for quadratic permutation polynomials over integers rings. IEEE Trans Inf Theory 52(3):1254–1260
Takeshita OY (2007) Permutation polynomial interleavers: an algebraic–geometric perspective. IEEE Trans Inf Theory 53(6):2116–2132
Rosnes E, Takeshita OY (2006) Optimum distance quadratic permutation polynomial-based interleavers for turbo codes, Proc. IEEE International Symposium on Information Theory (ISIT 2006), Seattle, USA, pp. 1988–1992.
Yuan J, Feng W, Vucetic B (2002) Performance of parallel and serial concatenated codes on fading channels. IEEE Trans Commun 50(10):1600–1608
http://www.tlc.polito.it/garello/turbodistance/turbodistance.html
Tarniceriu D, Trifina L, Munteanu V (2009) About minimum distance for QPP interleavers. Ann Telecommun 64(11–12):745–751
Zhao H, Fan P, Tarokh V (2010) On the equivalence of interleavers for turbo codes using quadratic permutation polynomials over integer rings. IEEE Commun Lett 14(3):236–238
Trifina L, Tarniceriu D (2013) Analysis of cubic permutation polynomials for turbo codes. Wireless Person Comm 69(1):1–22
Rosnes E (2012) On the minimum distance of turbo codes with quadratic permutation polynomial interleavers. IEEE Trans Inf Theory 58(7):4781–4795
Berrou C, Vaton S, Jezequel M, Douillard C (2002) Computing the minimum distance of linear codes by the error impulse method. IEEE Glob Telecommun Conf (GLOBECOM'02), Taipei Taiwan 2:1017–1020
Garello R, Vila-Casado A (2004) The all-zero iterative decoding algorithm for turbo code minimum distance computation. IEEE International Conference on Communications (ICC ‘04), Paris, France, pp.361–364
Crozier S, Guinand P, Hunt A (2005) Estimating the minimum distance of turbo-codes using double and triple impulse methods. IEEE Commun Lett 9(7):631–633
Crozier S, Guinand P, Hunt A (2007) Estimating the minimum distance of large-block turbo codes using iterative multiple-impulse methods. Eur Trans Telecommun 18(5):437–444
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Trifina, L., Tarniceriu, D. Improved method for searching interleavers from a certain set using Garello’s method with applications for the LTE standard. Ann. Telecommun. 69, 251–272 (2014). https://doi.org/10.1007/s12243-013-0360-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12243-013-0360-0