Abstract
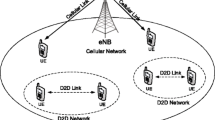
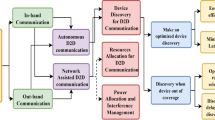
Proximity service (ProSe) enables the development of various applications that exploit proximity of the mobile devices. In ProSe, devices are expected to communicate with each other on device-to-device (D2D) links and make use of proximity information for the provision of a variety of services. An essential functionality in ProSe is the ability of a device to identify its neighbors. This process is referred to as D2D discovery. This paper investigates distributed D2D discovery based on greedy resource selection. In order to facilitate rapid and efficient distributed D2D discovery, we propose group-based peer discovery resource selection range restriction (GPSRR) scheme. GPSRR scheme disperses the devices concentrated at a certain discovery resource over multiple resources. This is done by limiting the resource selection of a device to a specified group of resources. We also propose group reselection (GR) scheme to resolve the unbalance of congestion among different groups of resources. Simulation results show that the proposed schemes can improve the speed of discovery and the number of discovered devices, especially in densely populated environments.









Similar content being viewed by others
Notes
The population of UEs considered in this work is realistic, particularly in the urban areas. The average population of mobile devices in New York city for the year 2010, for example, is 10,630 devices/1 km 2 [15].
In real environments, each UE can detect the collision in its occupied PDRs through the collision detection method given in Section 2.2
The trade-off between the gain of congestion dispersion and the loss of selection range restriction in determining N grp is discussed in Section 3.1.
References
3GPP (2013) TR 36.808: Evolved Universal Terrestrial Radio Access (E-UTRA); Carrier Aggregation; Base Station (BS) radio transmission and reception, Release-10, 8 July
3GPP (2010) TR 36.814: Evolved Universal Terrestrial Radio Access (E-UTRA); Further advancements for E-UTRA physical layer aspects, Release-9, 30 Mar
3GPP (2010) TR 36.806: Evolved Universal Terrestrial Radio Access (E-UTRA); Relay architectures for E-UTRA (LTE-Advanced), Release-9, 21 Apr
3GPP (2013) TS 36.300: Evolved Universal Terrestrial Radio Access (E-UTRA) and Evolved Universal Terrestrial Radio Access Network (E-UTRAN); Overall description, Release-11, 8 July
3GPP (2013) TR 22.803: Technical Specification Group Services and System Aspects; feasibility study for proximity services, Release-12, 15 Mar
McGlynn MJ, Borbash SA (2001) Birthday protocols for low energy deployment and flexible neighbor discovery in ad hoc wireless networks In Proceedings of ACM international symposium on Mobile ad hoc networking and computing, pp 137– 145
Galluccio L, Morabito G, Palazzo S (2004) Analytical evaluation of a tradeoff between energy efficiency and responsiveness of neighbor discovery in self-organizing ad hoc networks. IEEE J Sel Areas in Commun 22(7):1167–1182
Han SY, Lee D (2013) An adaptive hello messaging scheme for neighbor discovery in on-demand MANET routing protocols. IEEE Commun Lett 17(5):1040–1043
Cohen R, Kapchits B (2011) Continuous neighbor discovery in asynchronous sensor networks. IEEE/ACM Trans Networking 19(1):69–79
Baccelli F, Khude N, Laroia R, Li J, Richardson T, Shakkottai S, Tavildar S, Wu X (2012) On the design of device-to-device autonomous discovery In Proceedings of fourth international conference on communication systems and networks (COMSNETS), pp 1–9
3GPP (2013) TSG-RAN WG1 #73 R1-132503: Techniques for D2D discovery, 11 May
3GPP (2013) TS 36.211: Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA); Physical channels and modulation, Release-11, 26 June
Baccelli F, Blaszczyszyn B (2009) Stochastic geometry and wireless networks volume I: Theory. Foundations and trends in networking. NOW Publishers
Andrews JG, Baccelli F, Ganti RK (2011) A tractable approach to coverage and rate in cellular networks. IEEE Trans. Commun. 59(11):3122–3134
New Jersey place and county subdivision GCT-PH1. Population, housing units, area, and density: 2000. U.S. Census Bureau (2010)
ETSI (1998) TR 101 112: Selection procedures for the choice of radio transmission technologies of the UMTS Ver. 3.2.0, 20 Mar
3GPP (2014) TR 36.843: Technical Specification Group Radio Access Network; Study on LTE device to device proximity services; Radio aspects, Release-12, 21 Mar
3GPP (2013) TR 22.803: Technical Specification Group Services and System Aspects; Feasibility study for proximity services (ProSe), Release-12, 15 Mar
Cover T (1972) Broadcast channels. IEEE Trans of Inf Theory 18(1):2–14
Ogata K (2009) Modern control engineering, 5/e. Prentice Hall, Englewood Cliffs
Weber S, Andrews JG, Jindal N (2010) An overview of the transmission capacity of wireless networks. IEEE Trans Commun 58(12):3593–3604
Stoyan D, Kendall W, Mecke J (1996) Stochastic Geometry and Its Applications, 2/e. John Wiley and Sons, New York
Acknowledgements
This work was partially supported by Samsung Electronics and by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP) (2014R1A5A1011478).
Author information
Authors and Affiliations
Corresponding author
Appendix: Developing models for performance metrics in D2D discovery
Appendix: Developing models for performance metrics in D2D discovery
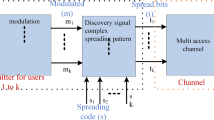
In order to analyze the impact of various parameters on the performance of distributed D2D discovery, we develop simple analytical model to derive the number of discoverable UEs. The analysis is performed based on the previous studies reported in [10, 13, 14], and [21]. It has been assumed that UEs are deployed in an area according to HPPP with intensity λ (UEs/m 2) [13]. A probing UE (UE 0) deployed at the center (0, 0) of the area performs discovery for other UEs. Euclidean distance from UE 0 to other UE k positioned at (x k , y k ) in \(\mathbb {R}^{2}\) is denoted by d k (=\(\sqrt {x{_{k}}{{~}^{2}}+y{_{k}}{{~}^{2}}}\)). Free-space path loss model with exponent α, where α is an integer larger than 2, and Rayleigh fading with mean 1 are considered. In addition, it has been assumed that each UE broadcasts discovery message with transmission power P tx [W]. In this case, the received power at UE 0 from another UE k is expressed as \(P_{\text {tx}} h_{k} d_{k}^{-\alpha }\) [W], where the random variable h k follows an exponential distribution with mean 1 [14]. For simplicity, we consider random PDR selection, where each UE randomly selects a PDR between [1, N PDR] with uniform distribution.
We firstly find detection probability P dct(d k ) in order to derive the number of detectable UEs [13, 21]. P dct(d k ) is defined as the probability that UE 0 will successfully receive discovery message sent by UE k which is d k [m] apart from the UE 0. The received SIR of the discovery message sent from UE k to UE 0 (SIR k ) should be larger than T SIR for successful decoding of the message. Thus, P dct(d k ) can be expressed as:
where Φ is a set of UE j, ∀j≠0 and k. Equation 10 is rewritten as follows:
Since cumulative distribution function of h k (\(\text {Pr}\left (h_{k} \leq b \right )\)) is 1−e −b [14], Eq. (11) can be rewritten as follows:
where h j and d j are independent random variables. Thus, Eq. (12) becomes:
Through calculating the expectation for h j which follows an exponential distribution with mean 1, Eq. (13) can be rewritten as follows:
By using the probability generating function for PPP [22], Eq. (14) is approximated to:
Let us denote \(x_{j} = d_{k} T_{\text {SIR}}^{1/ \alpha } r_{j} \cos \theta _{j}\) and \(y_{j} = d_{k} T_{\text {SIR}}^{1/ \alpha } r_{j} \sin \theta _{j}\). Then, we can find \(dx_{j} dy_{j} = {d^{2}_{k}} T^{2/\alpha }_{\text {SIR}} r_{j} dr_{j} d\theta _{j}\) and \({x^{2}_{j}}+{y^{2}_{j}}={d^{2}_{k}} T^{2/\alpha }_{\text {SIR}} {r_{j}^{2}}\). By substituting these into Eq. (15), we can obtain:
Through solving the integration for 𝜃 j , Eq. (16) is simplified as follows:
By using the techniques of complex analysis, we can find that the integration \({\int }^{\infty }_{0} {r_{j}}/\left ({r_{j}^{\alpha } + 1}\right ) d r_{j}\) equals to \(\pi / \left (\alpha \cdot \sin (2\pi / \alpha ) \right )\). Finally, the detection probability for UE k is obtained as follows:
Detectable area of UE k is defined as an area where the UE 0 can successfully receive discovery message from the UE k [13]. Mean detectable area for UE k (\(\tilde {A}_{k} \left ({\Phi }, T_{\text {SIR}} \right )\) [m 2]) is expressed as follows:
Averaging \(\tilde {A}_{k} \left ({\Phi }, T_{\text {SIR}} \right )\) for all possible positions of UE k, we can obtain the mean volume of the detectable area for UE intensity λ as
Let us denote the intensity of UEs occupying a PDR i as λ i [UEs/m 2]. The mean number of discoverable UEs in a PDR i can be obtained by multiplying \(\tilde {A} \left (\lambda _{i} \right )\) [m 2] with λ i [UEs/m 2] as:
Finally, the mean number of discoverable UEs in a discovery period consisting of N PDR PDRs is obtained as:
Rights and permissions
About this article
Cite this article
Bae, S.J., Gu, J., Hasan, S.F. et al. Congestion dispersion in device-to-device discovery for proximity-based services. Ann. Telecommun. 70, 275–287 (2015). https://doi.org/10.1007/s12243-014-0448-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12243-014-0448-1