Relay selection in two-way full-duplex relay networks over Nakagami-m fading channels

Abstract

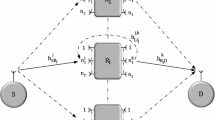
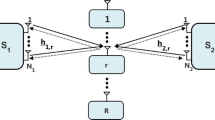
We analyze the outage performance of relay selection in two-way full-duplex amplify-and-forward cooperative systems in the presence of residual loop-interference (LI) over Nakagami-m fading channels. In the proposed system, a relay node is selected according to max-min policy and the physical-layer-network-coding technique is applied for two-way transmission. By using end-to-end signal-to-interference-plus-noise-ratio, a new exact outage probability expression is derived in a single-integral form. The numerical and Monte-Carlo simulation results verify the analysis. Moreover, lower-bound and asymptotic expressions for the outage probability are obtained in closed-form. The numerical results reveal that the max-min selection policy provides a significant performance improvement for two-way full-duplex relaying. We observe that the outage performance can be enhanced as long as either the number of relay nodes, the transmit power, or the efficiency of the LI cancellation process increases.

Appendix: Proof of Eq. 10

By using [9, Eq. (35)], the CDF of γ _{i, b} can be given by

$$\begin{array}{@{}rcl@{}} {F_{{\gamma_{i,b}}}}\left( z \right) &=& \sum\limits_{c = 1}^{N} {\int\limits_{x = 0}^{z} {{f_{{\gamma_{i,c}}}}\left( x \right)\Pr \left( {x \le {\gamma_{j,c}}} \right)} }\\ &&\times\prod\limits_{p = 1\hfill\atop p \ne c\hfill}^{N} {\Pr } \left[ {\min \left( {{\gamma_{i,p}},{\gamma_{j,p}}} \right) \le x} \right]dx\\ &&+ \sum\limits_{c = 1}^{N} {\int\limits_{x = 0}^{z} {{f_{{\gamma_{i,c}}}}\left( x \right)} } \Pr \left( {x > {\gamma_{j,c}}} \right) \\ &&\times \prod\limits_{p = 1\hfill\atop p \ne c\hfill}^{N} {\Pr } \left[ {\min \left( {{\gamma_{i,p}},{\gamma_{j,p}}} \right) \le {\gamma_{j,c}}} \right]dx\\ &=& N\int\limits_{x = 0}^{z} {{f_{{\gamma_{i,c}}}} \left( x \right) \left[ {{{\bar F}_{{\gamma_{i,c}}}} \left( x \right) {{\left( {1 - \bar F_{{\gamma_{i,c}}}^{2} \left( x \right)} \right)}^{N - 1}}} \right.}\\ &&+ \int\limits_{y = 0}^{x} {{f_{{\gamma_{i,c}}}} \left( y \right)} \left. {{{\left( {1 - \bar F_{{\gamma_{i,c}}}^{2} \left( y \right)} \right)}^{N - 1}}dy} \right]dx \end{array} $$

(39)

where ${\bar F}_{{\gamma _{i,c}}}\left (\cdot \right )=1-F_{{\gamma _{i,c}}}\left (\cdot \right )$. By substituting the PDF and CDF expressions of γ _{i, c} given in Section 2.1, the above expression is rewritten as

$$\begin{array}{@{}rcl@{}} {F_{{\gamma_{i,b}}}}\left( z \right) &=& \frac{{N{\mu^{m}}}}{{{\Gamma} \left( m \right)}}\int\limits_{x = 0}^{z} {\frac{{{x^{m - 1}}{\Gamma} \left( {m,\mu x } \right)}}{{{e^{\mu x }}{\Gamma} \left( m \right)}}{{\left[ {1 - {{\left( {\frac{{{\Gamma} \left( {m, \mu x } \right)}}{{{\Gamma} \left( m \right)}}} \right)}^{2}}} \right]}^{N - 1}}}\\ &&+ \frac{{{x^{m - 1}}{\mu^{m}}}}{{{e^{\mu x }}{\Gamma} \left( m \right)}}\int\limits_{y = 0}^{x} {\frac{{{y^{m - 1}}}}{{{e^{\mu y }}}}} {\left[\! {1 \!- {{\left( {\frac{{{\Gamma} \left( {m,\mu y } \right)}}{{\Gamma \left( m \right)}}} \right)}^{2}}} \right]^{N - 1}}dydx\\ \end{array} $$

(40)

where Γ(⋅,⋅) is the upper incomplete Gamma function [16, Eq. (8.350.2)]. For the integer values of m, by using binomial expansion and [16, Eq. (8.352.4)],

$$ \begin{array}{llllll} F&_{{\gamma_{i,b}}}\left( z \right) = \frac{{N{\mu^{m}}}}{{{\Gamma} \left( m \right)}}\sum\limits_{k = 0}^{N - 1} {\left( {\begin{array}{*{20}{c}} {N - 1}\\ k \end{array}} \right){{\left( { - 1} \right)}^{k}}} \\ &\times \underbrace {\left\{ {\int\limits_{x = 0}^{z} {\frac{{{x^{m - 1}}}}{{{e^{\left( {2k + 2} \right)\mu x}}}}{{\left[ {\sum\limits_{q = 0}^{m - 1} {\frac{{{{\left( {\mu x} \right)}^{q}}}}{{q!}}} } \right]}^{2k + 1}}} } dx \right.}_{{I_{3}}} + \frac{{{\mu^{m}}}}{{{\Gamma} \left( m \right)}}\\ &\times \underbrace {\left. {\int\limits_{x = 0}^{z} {\frac{{{x^{m - 1}}}}{{{e^{\mu x}}}}\int\limits_{y = 0}^{x} {\frac{{{y^{m - 1}}}}{{{e^{\left( {2k + 1} \right)\mu y}}}}} {{\left[ {\sum\limits_{q = 0}^{m - 1} {\frac{{{{\left( {\mu y} \right)}^{q}}}}{{q!}}} } \right]}^{2k}}dy} dx} \right\}}_{{I_{4}}} \end{array} $$

(41)

can be obtained. For the solution of the first integration I ₃, we need to use multinomial coefficients as in [17, Eq. (7)] and [16, Eq. (3.351.1)]. Then, I ₃ is found as

$$\begin{array}{@{}rcl@{}} {I_{3}} &=& \sum\limits_{t = 0}^{{\theta_{1}}} {{\Phi}_{t}^{2k + 1}{\mu^{t}}\int\limits_{x = 0}^{z} {\frac{{{x^{t + m - 1}}}}{{{e^{\left( {2k + 2} \right)\mu x}}}}dx} } \\ &=& \sum\limits_{t = 0}^{{\theta_{1}}} {\frac{{{\Phi}_{t}^{2k + 1}\gamma \left[ {t + m,\left( {2k + 2} \right)\mu z} \right]}}{{{\mu^{m}}{{\left( {2k + 2} \right)}^{t + m}}}}} \end{array} $$

(42)

where 𝜃 ₁ = (2k + 1)(m − 1) and ${\Phi }_{t}^{2k+1}$ is the coefficient of (μx)^t in the expansion of

$$ {{{\left[ {\sum\limits_{q = 0}^{m - 1} {\frac{{{{\left( {\mu x} \right)}^{q}}}}{{q!}}} } \right]}^{2k + 1}}}. $$

(43)

The other expression I ₄ is composed of double-integrals. The inner integration inside I ₄ can be found by following the same steps applied to I ₃ and it is given by

$$ {I_{4}} = \sum\limits_{t = 0}^{{\theta_{2}}} {\frac{{{\Phi}_{t}^{2k}{\mu^{- m}}}}{{{{\left( {2k + 1} \right)}^{t + m}}}}} \int\limits_{x = 0}^{z} {\frac{{\gamma \left[ {t + m,\left( {2k + 1} \right)\mu x} \right]}}{{{x^{1 - m}}{e^{\mu x}}}}} dx $$

(44)

where 𝜃 ₂ = 2k(m − 1) and ${\Phi }_{t}^{2k}$ is also the coefficient of (μy)^t in the expansion of

$$ {{{\left[ {\sum\limits_{q = 0}^{m - 1} {\frac{{{{\left( {\mu y} \right)}^{q}}}}{{q!}}} } \right]}^{2k}}}. $$

(45)

By applying both [16, Eq. (8.352.6)] and [16, Eq. (3.351.1)], respectively, I ₄ can be easily found in a closed-form as

$$\begin{array}{@{}rcl@{}} {I_{4}} &=& \sum\limits_{t = 0}^{{\theta_{2}}} {\frac{{{\Phi}_{t}^{2k}{\Gamma} \left( {m + t} \right)}}{{{\mu^{2m}}{{\left( {2k + 1} \right)}^{t + m}}}}} \\ &&\times \left[ {\gamma \left( {m,\mu z} \right) - \sum\limits_{v = 0}^{t + m - 1} {\frac{{\gamma \left[ {m + v,\left( {2k + 2} \right)\mu z} \right]}}{{v!{{\left( {2k + 2} \right)}^{m + v}}{{\left( {2k + 1} \right)}^{- v}}}}} } \right].\!\\ \end{array} $$

(46)

Finally, the CDF of γ _{i, b} given in Eq. 10 can be obtained by substituting (42) and (46) into (41).