Abstract
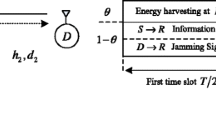
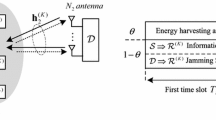
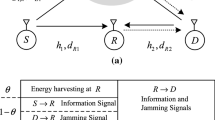
In this paper, we study the impact of hardware impairments, which can act as one of the factors that cause degradation in the performance of communication systems, on the secrecy capacity of an untrusted relaying wireless energy-harvesting (WEH) system. In the system, the energy-constrained relay is an untrusted node which can overhear the source’s confidential signal while assisting the source-destination communication. The relay operates in the amplify-and-forward (AF) mode and uses the power-splitting (PS) protocol for harvesting energy. The destination sends an artificial noise (AN) signal during the source-relay communication. The AN signal acts as an additional energy source and an interference source at the relay. In our study, we derive an approximation of the average secrecy capacity (ASC) for the high-power-regime approximation in order to evaluate the secrecy performance of the proposed system, which is also the upper bound for the ASC. The analytical results are confirmed via Monte Carlo simulations. The numerical results provide valuable insights into the effect of the various system parameters, such as the power-splitting ratio, the relay’s location, the trade-off between the source’s power and the destination’s power, and the level of hardware impairments, on the secrecy performance.





Similar content being viewed by others
Notes
The values of \(\sigma _{[a]}^{2}\) and \(\sigma _{[c]}^{2}\) are not necessarily the same and can be found in the receiver’s specification documents.
References
Ding Z., Perlaza S. M., Esnaola I., Poor H. V. (2014) Power allocation strategies in energy harvesting wireless cooperative networks. IEEE Trans. Wireless Commun. 13(2):846–860
Nasir A., Zhou X., Durrani S., Kennedy R (2015) Wireless-powered relays in cooperative communications: time-switching relaying protocols and throughput analysis. IEEE Trans. Commun. 63:1607–1622
Zhu G., Zhong C., Suraweera H., Karagiannidis G., Zhang Z., Tsiftsis T. (2015) Wireless information and power transfer in relay systems with multiple antennas and interference. IEEE Trans. Commun. 63:1400–1418
Hu L., et al. (2018) Cooperative jamming for physical layer security enhancement in internet of things. IEEE Internet Things J. 5(1):219–228
Liu Y., Chen H. H., Wang L. (2017) Physical layer security for next generation wireless networks: theories, technologies, and challenges. IEEE Commun. Surv. Tutorial. 19(1):347–376
Lee J., Choi W. (2014) Multiuser diversity for secrecy communications using opportunistic jammer selection: Secure DoF and jammer scaling law. IEEE Trans. Signal Process. 62:828–839
Xing H., Liu L., Zhang R. (2016) Secrecy wireless information and power transfer in fading wiretap channel. IEEE Trans. Veh. Technol. 65:180–190
Liu L., Zhang R., Chua K. C. (2014) Secrecy wireless information and power transfer with MISO beamforming. IEEE Trans. Signal Process. 62:1850–1863
Zhang H., Li C., Huang Y., Yang L. (2015) Secure beamforming for SWIPT in multiuser MISO broadcast channel with confidential messages. IEEE commun. lett. 19:1347–1350
Hoang T. M., Duong T. Q., Vo N.S., Kundu C. (2017) Physical layer security in cooperative energy harvesting networks with a friendly jammer. IEEE Wireless Commun. Lett., (Accepted)
Kalamkar S. S., Banerjee A. (2017) Secure communication via a wireless energy harvesting untrusted relay. IEEE Trans. Veh. Technol. 66:2199–2213
Björnson E., Matthaiou M., Debbah M. (2013) A new look at dual-hop relaying: performance limits with hardware impairments. IEEE Trans. Commun. 61:4512–4525
Mokhtar M., Boulogeorgos A. A., Karagiannidis G., Al-Dhahir N. (2014) OFDM opportunistic relaying under joint transmit/receive I/Q imbalance. IEEE Trans. Commun. 62:1458– 1468
Zhang X., Matthaiou M., Coldrey M., Björnson E. (2015) Impact of residual transmit RF impairments on training-based MIMO systems. IEEE Trans. Commun. 63:2899–2911
Duy T. T., Duong T., Costa D. B., Bao V. N. Q., Elkashlan M. (2015) Proactive relay selection with joint impact of hardware impairment and co-channel interference. IEEE Trans. Commun. 63:1594–1606
Zhou X., Zhang R., Ho C. K. (2013) Wireless information and power transfer: architecture design and rate-energy tradeoff. IEEE Trans. Commun. 61:4754–4767
Gradshteyn I.S., Ryzhik I. M. (2007) Table of integrals, series and products, 7th edn. Academic Press, New York
Khafagy M. G., Ismail A., Alouini M. S., Aïssa S. (2015) Efficient cooperative protocols for full duplex relaying over Nakagami-m fading channels. IEEE Trans. Wireless Commun. 14(6):3456–3470
Holma H., Toskala A. (2011) LTE for UMTS: evolution to LTE-advanced, 2nd edn. Wiley, New Yorks
Nasir A. A., Zhou X., Durrani S., Kennedy R. A. (2013) Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 12(7):3622– 3636
Zhu G., Zhong C., Suraweera H. A., Zhang Z., Yuen C., Yin R. (2014) Ergodic capacity comparison of different relay precoding schemes in dual-hop AF systems with co-Channel interferer. IEEE Trans. Commun. 62(7):2314–2328
Acknowledgments
This work was supported by the 2021 Research Fund of University of Ulsan.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A:: Proof of Proposition 1
From Eq. (16), \(F_{\gamma _{\{r,d\}}}\left (\gamma \right )|_{\gamma < \tfrac {1}{\mathcal AC}}\) can be rewritten as
Using the PDF of X2 given by \(f\left ({{m_{2}},{{\bar \gamma }_{2}};x} \right )\) and the CDF of X1 given by \(F\left ({{m_{1}},{{\bar \gamma }_{1}};x} \right )\), Eq. (16) can be rewritten as
With the help of [17, Eq. (3.381.4)], Eq. (28) can be expressed as given in Eq. (17).
Appendix B: Proof of Proposition 2
2.1 B.1 The calculation of \(\mathcal {J}_{1}\)
In case 1 (\(\mu {\mathcal C}=1\)), \({\mathcal I}\left (\gamma \right )\) can be decomposed by using the partial-fraction expansion method as
where the values of b1 and b2,j are determined by
The expression of b2,j in Eq. (31) can be simplified by Eq. (22).
Then, \(\mathcal J\) can be calculated by
Finally, \({\mathcal J}_{1}\) can be expressed as in Eq. (21).
2.2 B.2 The calculation of \(\mathcal {J}_{2}\)
In case 2 (\(\mu {\mathcal C}=0\)), \({\mathcal I} \left (\gamma \right )\) can be decomposed by using the partial-fraction expansion method as
where the values of b3 and b4,j are determined by
The expression of b4,j in Eq. (35) can be simplified by Eq. (24).
Then, \(\mathcal J\) can be calculated by
Finally, \({\mathcal J}_{2}\) can be expressed as in Eq. (23).
2.3 B.3 The calculation of \(\mathcal {J}_{3}\)
In ccase 3 (\(\mu {\mathcal C} \notin \{0,1\}\)), \({\mathcal I}\left (\gamma \right )\) can be decomposed by using the partial-fraction expansion method as
where the values of b5, b6, and b7,j are determined by
By following similar calculations as in Eqs. (31) and (35), the expression of b4,j in Eq. (42) can be simplified by Eqs. (26). Then, \(\mathcal {J}\) can be calculated by
Finally, \(\mathcal {J}_{3}\) can be expressed as in Eq. (25).
Rights and permissions
About this article
Cite this article
Tuan, V.P., Kong, H.Y. Secrecy capacity analysis of untrusted relaying energy-harvesting systems with hardware impairments. Ann. Telecommun. 75, 397–405 (2020). https://doi.org/10.1007/s12243-020-00758-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12243-020-00758-3