Skip to main content
Springer Nature Link
Log in

Joint transmit and receive beamforming for MIMO interference channels using the difference of convex programming

  • Published:
Annals of Telecommunications Aims and scope Submit manuscript

Abstract

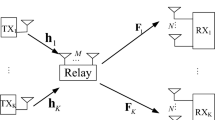
Interference alignment (IA) techniques raise the achievable degree of freedom (DoF) in wireless interference networks by designing the aligned transceiver beamformers. The DoF shows the number of interference-free data streams that can be communicated simultaneously on a channel. To achieve the maximum possible DoF, we design the aligned beamformers in this study based on the interference leakage minimization (ILM) method for a multiple-input multiple-output interference channel (MIMO-IC). Accordingly, the ILM optimization problem is firstly relaxed to the rank constrained semidefinite programming (SDP) problems. Next, using a non-convex programming method (i.e., the difference of convex [DC] programming method), the proposed non-convex rank constrained SDP problem is reformulated to the DC form. We propose a novel DC-based IA algorithm that designs the optimized aligned beamformers based on an iterated local search using a penalty function. By increasing the penalty factor, the solution of the penalized DC problem converges to the solution of the original DC problem. Unlike the previous IA approaches, the proposed DC-based IA algorithm optimizes transmit and receive beamformers jointly and simultaneously in each iteration (i.e., not alternately). Simulation results indicate that the proposed method outperforms the previous competitive IA algorithms by providing more throughputs and less interference leakage as compared to the least-squares (LS)-based and the minimum mean square error (MMSE)–based IA algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Cadambe VR, Jafar SA (2008) Interference alignment and spatial degrees of freedom for the k user interference channel. In: Proc. 2008 IEEE International Conference on Communications, Beijing, pp 971–975

  2. Jafar SA, Shamai S (2008) Degrees of freedom region of the MIMO X Channel. IEEE Trans Inf Theory 54(1):151–170

    Article  MathSciNet  Google Scholar 

  3. Maddah-Ali MA, Motahari AS, Khandani AK (2008) Communication over MIMO X channels: interference alignment, decomposition, and performance analysis. IEEE Trans Inf Theory 54(8):3457–3470

    Article  MathSciNet  Google Scholar 

  4. Razaviyan M, Sanjabi M, Luo Z-Q (2012) Linear transceiver design for interference alignment: complexity and computation. IEEE Trans Inf Theory 58(5):2896–2910

    Article  MathSciNet  Google Scholar 

  5. Gomadam K, Cadambe VR, Jafar SA (2008) Approaching the capacity of wireless networks through distributed interference alignment. In: Proc IEEE Global Telecomm Conf, New Orleans, pp 1–6

  6. Papailiopoulos DS, Dimakis AG (2012) Interference alignment as a rank constrained rank minimization. IEEE Trans Signal Process 60(8):4278–4288

    Article  MathSciNet  Google Scholar 

  7. Du H, Ratnarajah T, Sellathurai M, Papadias CB (2013) Reweighted nuclear norm approach for interference alignment. IEEE Trans Commun 61(9):3754–3765

    Article  Google Scholar 

  8. Razavi SM, Ratnarajah T (2014) Performance analysis of interference alignment under CSI mismatch. IEEE Trans Veh Technol 63(9):4740–4748

    Article  Google Scholar 

  9. Sridharan G, Yu W (2015) Linear beamformer design for interference alignment via rank minimization. IEEE Trans Signal Process 63(22):5910–5923

    Article  MathSciNet  Google Scholar 

  10. Razavi SM, Ratnarajah T (2016) Adaptive LS- and MMSE-based beamformer design for multiuser MIMO interference channels. IEEE Trans Veh Technol 65(1):132–144

    Article  Google Scholar 

  11. Razavi SM (2018) Beamformer design for MIMO interference broadcast channels with semidefinite programming. IEEE Trans Signal Process 66(17):4504–4515

    Article  MathSciNet  Google Scholar 

  12. Ruan L, Win MZ, Lau VKN (2013) Designing interference alignment algorithms by algebraic geometry analysis. In: Proc. IEEE Global Commun Conf (GLOBECOM), Atlanta, pp 1796–1801

  13. Peters SW, Heath RW (2010) Cooperative algorithms for MIMO interference channels. IEEE Trans Veh Technol 60(1):206–218

    Article  Google Scholar 

  14. Li Y, Dia X, Dong Q (2017) Spatial–degree of freedom improvement of interference alignment in multi-input, multi-output interference channels. Int J Distrib Sens Netw 13(1):1–11

    Google Scholar 

  15. Razaviyan M, Lyubeznik G, Luo Z-Q (2012) On the degrees of freedom achievable through interference alignment in a MIMO interference channel. IEEE Trans Signal Process 60(2):812–821

    Article  MathSciNet  Google Scholar 

  16. González O, Beltrán C, Santamaria I (2014) A feasibility test for linear interference alignment in MIMO channels with constant coefficients. IEEE Trans Inf Theory 60(3):1840–1856

  17. Bresler DCG, Tse D (2014) Feasibility of interference alignment for the MIMO interference channel. IEEE Trans Inf Theory 60(9):5573–5586

    Article  MathSciNet  Google Scholar 

  18. Luo ZQ, Ma WK, So AM, Ye Y, Zhang S (2010) Semidefinite relaxation of quadratic optimization problems. IEEE Signal Process Mag 27(3):20–34

    Article  Google Scholar 

  19. Piot MGB, Pietquin O (2016) Difference of convex functions programming applied to control with expert data. Available on: http://arxiv.org/abs/1606.01128v2. Accessed 17 Jan 2020

  20. Thi HAL, Dinh TP (2005) The DC (difference of convex functions) programming and DCA revisited with DC models of real world non-convex optimization problems. Ann Oper Res 133(1–4):23–46

    MathSciNet  MATH  Google Scholar 

  21. Wu Y, Ng DWK, Wen CK, Schober R, Lozano A (2017) Low-complexity MIMO precoding for finite-alphabet signals. IEEE Trans Wirel Commun 16(7):4571–4584

    Article  Google Scholar 

  22. Ketseoglou T, Ayanoglu E (2018) Downlink precoding for massive MIMO systems exploiting virtual channel model sparsity. IEEE Trans Commun 66(5):1925–1939

    Article  Google Scholar 

  23. Ketseoglou T, Ayanoglu E (2019) Zero-forcing per-group precoding (ZF-PGP) for robust optimized downlink massive MIMO performance. IEEE Trans Commun 67(10):6816–6828

    Article  Google Scholar 

  24. Strang G (2016) Introduction to linear algebra, 5th edn. Wellesley-Cambridge Press and SIAM, New York

    MATH  Google Scholar 

  25. Wolkowicz H, Saigal R, Vandenberghe L (2000) Handbook of Semidefinite programming-theory, algorithms, and applications. Springer, Berlin

    Book  Google Scholar 

  26. Morency MW, Vorobyov SA (2016) An algebraic approach to a class of rank-constrained semidefinite programs with applications. Available on: https://arxiv.org/abs/1610.02181. Accessed 25 Jan 2020

  27. Mahboobi B, Soleimani-Nasab E, Ardebilipour M (2014) Outage probability based robust distributed beam-forming in multi-user cooperative networks with imperfect CSI. Wirel Pers Commun 77(3):1629–1658

    Article  Google Scholar 

  28. Boyd S, Vandenberghe L (2004) Convex optimization. New York, Cambridge

    Book  Google Scholar 

  29. Hjorungnes A, Gesbert D (2007) Complex-valued matrix differentiation: techniques and key results. IEEE Trans Signal Process 55(6):2740–2746

    Article  MathSciNet  Google Scholar 

  30. Cao P, Thompson JS, Poor IV (2017) A sequential constraint relaxation algorithm for rank-one constrained problems. In: Proc IEEE European Signal Processing Conference (EUSIPCO), Kos, Greece, pp 1060–1064

  31. Grant M, Boyd S, Ye Y (2009) CVX: Matlab software for disciplined convex programming. Available on: http://www.stanford.edu/˜boyd/cvx. Accessed 12 Nov 2019

  32. CVX Research (2012) Matlab software for disciplined convex programming, version 2.0 beta. Available on: http://cvxr.com/cvx. Accessed 12 Nov 2019

  33. Grant MC, Boyed SP (2008) Graph implementations for non-smooth convex programs. In: Blondel VD, Boyd SP, Kimura H (eds) Recent Advances in Learning and Control. Lecture Notes in Control and Information Sciences, vol 371. Springer, London, pp 95–110

  34. Yetis C, Gou T, Jafar S, Kayran A (2010) On feasibility of interference alignment in MIMO interference networks. IEEE Trans Signal Process 58(9):4771–4782

    Article  MathSciNet  Google Scholar 

  35. Gollakota S, Perli SD, Katabi D (2009) Interference alignment and cancellation. In: Proc ACM SIGCOMM Conference on Data Communication, Barcelona, pp 159–170

  36. Ali E, Ismail M, Nordin R, Abdulah NF (2017) Beamforming techniques for massive MIMO systems in 5G: overview, classification, and trends for future research. Front Inform Technol Electron Eng 18:753–772

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Islamic Azad University, South Tehran Branch, Tehran, Iran

    Negin Danesh & Mansour Sheikhan

  2. Department of Electrical and Computer Engineering, Communication, Computer, and Industrial Network Research Center, Islamic Azad University, Science and Research Branch, Tehran, Iran

    Behrad Mahboobi

Authors
  1. Negin Danesh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mansour Sheikhan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Behrad Mahboobi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mansour Sheikhan.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Danesh, N., Sheikhan, M. & Mahboobi, B. Joint transmit and receive beamforming for MIMO interference channels using the difference of convex programming. Ann. Telecommun. 76, 787–800 (2021). https://doi.org/10.1007/s12243-020-00829-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12243-020-00829-5

Keywords