Abstract
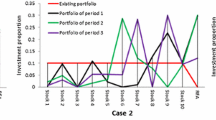
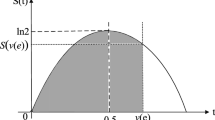
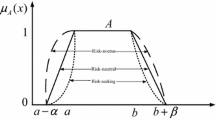
In this paper we propose multicriteria credibilistic framework for portfolio rebalancing (adjusting) problem with fuzzy parameters considering return, risk and liquidity as key financial criteria. The portfolio risk is characterized by a risk curve that represents each likely loss of the portfolio return and the corresponding chance of its occurrence rather than a single pre-set level of the loss. Furthermore, we consider an investment market scenario where, at the end of a typical time period, the investor would like to modify his existing portfolio by buying and/or selling assets in response to changing market conditions. We assume that the investor pays transaction costs based on incremental discount schemes associated with the buying and/or selling of assets, which are adjusted in the net return of the portfolio. A hybrid intelligent algorithm that integrates fuzzy simulation with a real-coded genetic algorithm is developed to solve the portfolio rebalancing (adjusting) problem. The proposed solution approach is useful particularly for the cases where fuzzy parameters of the problem are characterized by general functional forms.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bhattacharyya R, Kar S, Majumder DD (2011) Fuzzy mean-variance-skewness portfolio selection models by interval analysis. Comput Math Appl 61:126–137
Carlsson C, Fullér R, Majlender P (2002) Majlender. Fuzzy Set Syst 131:13–21
Charnes A, Cooper WW (1961) Management models and industrial applications of linear programming. Wiley, New York
Chellathurai T, Draviam T (2005) Dynamic portfolio selection with nonlinear transaction costs. Proc R Soc A 461:3183–3212
Chen JS, Hou JL, Wu SM, Chang-Chien YW (2009) Constructing investment strategy portfolios by combination genetic algorithms. Expert Syst Appl 36:3824–3828
Chen W (2009) Weighted portfolio selection models based on possibility theory. Fuzzy Inf Eng 2:115–127
Choi UJ, Jang BG, Koo HK (2007) An algorithm for optimal portfolio selection problems with transaction costs and random lifetimes. Appl Math Comput 191:239–252
Dong W, Peng J (2009) Credibilistic risk optimization models and algorithms. In: Proceedings of the international conference on computational intelligence and natural computing IEEE, pp 378–381
Fang Y, Lai KK, Wang SY (2006) Portfolio rebalancing model with transaction costs based on fuzzy decision theory. Eur J Oper Res 175:879–893
Gupta P, Mehlawat MK, Saxena A (2008) Asset portfolio optimization using fuzzy mathematical programming. Inform Sci 178:1734–1755
Gupta P, Mehlawat MK, Saxena A (2010) A hybrid approach to asset allocation with simultaneous consideration of suitability and optimality. Inform Sci 180:2264–2285
Gupta P, Inuiguchi M, Mehlawat MK (2011) A hybrid approach for constructing suitable and optimal portfolios. Expert Syst Appl 38:5620–5632
Gupta P, Mehlawat MK, Mittal G (2012) Asset portfolio optimization using support vector machines and real- coded genetic algorithm. J Global Optim 53:297–315
Hasuike T, Katagiri H, Ishii H (2009) Portfolio selection problems with random fuzzy variable returns. Fuzzy Set Syst 160:2579–2596
Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor
Huang X (2007) Portfolio selection with fuzzy returns. J Intell Fuzzy Syst 18:383–390
Huang X (2008) Risk curve and fuzzy portfolio selection. Comput Math Appl 55:1102–1112
Huang X (2009) A review of credibilistic portfolio selection. Fuzzy Optim Decis Making 8:263–281
Huang X (2012) An entropy method for diversified fuzzy portfolio selection. Int J Fuzzy Syst 14:160–165
Inuiguchi M, Ramik J (2000) Possibilistic linear programming: a brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Set Syst 111:3–28
Inuiguchi M, Tanino T (2000) Portfolio selection under independent possibilistic information. Fuzzy Set Syst 115:83–92
Jacob NL (1974) A limited-diversification portfolio selection model for the small investor. J Finance 29:847–856
Jana P, Roy TK, Mazumder SK (2009) Multi-objective possibilistic model for portfolio selection with transaction cost. J Comput Appl Math 228:18–196
Kozhan R, Schmid W (2009) Asset allocation with distorted beliefs and transaction costs. Eur J Oper Res 194:236–249
Li X, Liu B (2006) A sufficient and necessary condition for credibility measures. Int J Uncertain Fuzz 14:527–535
Li X, Zhang Y, Wong HS, Qin Z (2009) A hybrid intelligent algorithm for portfolio selection problem with fuzzy returns. J Comput Appl Math 233:264–278
Li X, Qin Z, Kar S (2010) Mean-Variance-Skewness model for portfolio selection with fuzzy returns. Eur J Oper Res 202:239–247
Li X, Shou B, Qin Z (2012) An expected regret minimization portfolioselection model. Eur J Oper Res 218:484–492
Li Y, Wang B, Watada J (2011) Building a fuzzy multi-objective portfolio selection model with distinct risk measurements. In: Proceedings of the IEEE international conference on fuzzy systems (FUZZ-IEEE 2011), pp 1096–1102
Liu B (2002) Theory and Practice of Uncertain Programming. Physica-Verlag, Heidelberg
Liu B, Liu YK (2002) Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans Fuzzy Syst 10:445–450
Liu B (2006) A survey of credibility theory. Fuzzy Optim Decis Making 5:387–408
Luengo EA (2010) Fuzzy mean-variance portfolio selection problems. Adv Model Optim 12:399–410
Mao JCT (1970) Essentials of portfolio diversification strategy. J Finance 25:1109–1121
Markowitz HM (1952) Portfolio selection. J Finance 7:77–91
Morton AJ, Pliska SR (1995) Optimal portfolio management with fixed transaction costs. Math Finance 5:337–356
Murata T, Ischibuchi H (1995) MOGA: multi-objective genetic algorithms. In: Proceedings of the second IEEE international conference on, evolutionary computation, pp 289–294
Wang SY, Zhu SS (2002) On fuzzy portfolio selection problem. Fuzzy Optim Decis Making 1:361–377
Yoshida Y (2009) An estimation model of value-at-risk portfolio under uncertainity. Fuzzy Set Syst 160:3250–3262
Yu JR, Lee WY (2011) Portfolio rebalancing model using multiple criteria. Eur J Oper Res 209:166–175
Zadeh LA (1965) Fuzzy sets Inform Contr 8:338–353
Zadeh LA (2005) Towards a generalized theory of uncertainity (GTU)-an outline. Inform Sci 172:1–40
Zhang WG, Wang YL, Chen ZP, Nie ZK (2007) Possibilistic mean-variance models and efficient frontiers for portfolio selection problem. Inf Sci 177:2787–2801
Zhang WG, Zhang X, Xu W (2010) A risk tolerance model for portfolio adjusting problem with transaction costs based on possibilistic moments. Insur Math Econ 46:496–499
Zhang WG, Zhang X, Chen Y (2011) Portfolio adjusting optimization with added assets and transaction costs based on credibility measures. Insur Math Econ 49:353–360
Zhang X, Zhang WG, Cai R (2010) Portfolio adjusting optimization under credibility measures. J Comput Appl Math 234:1458–1465
Zhang Y, Li X, Wong H-S, Tan L (2009) Fuzzy multi-objective portfolio selection model with transaction costs. In: Proceedings of the IEEE international conference on fuzzy systems (FUZZ-IEEE 2009), pp 273–278
Acknowledgments
We are thankful to the Editor-in-chief, Guest Editor and the anonymous referees for their valuable comments and suggestions to improve presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gupta, P., Mittal, G. & Mehlawat, M.K. A multicriteria optimization model of portfolio rebalancing with transaction costs in fuzzy environment. Memetic Comp. 6, 61–74 (2014). https://doi.org/10.1007/s12293-012-0102-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12293-012-0102-2